论文提出NF-ResNet,根据网络的实际信号传递进行分析,模拟BatchNorm在均值和方差传递上的表现,进而代替BatchNorm。论文实验和分析十分足,出来的效果也很不错。一些初始化方法的理论效果是对的,但实际使用会有偏差,论文通过实践分析发现了这一点进行补充,贯彻了实践出真知的道理
来源:晓飞的算法工程笔记 公众号
论文: Characterizing signal propagation to close the performance gap in unnormalized ResNets
Introduction
BatchNorm是深度学习中核心计算组件,大部分的SOTA图像模型都使用它,主要有以下几个优点:
- 平滑损失曲线,可使用更大的学习率进行学习。
- 根据minibatch计算的统计信息相当于为当前的batch引入噪声,有正则化作用,防止过拟合。
- 在初始阶段,约束残差分支的权值,保证深度残差网络有很好的信息传递,可训练超深的网络。
然而,尽管BatchNorm很好,但还是有以下缺点:
- 性能受batch size影响大,batch size小时表现很差。
- 带来训练和推理时用法不一致的问题。
- 增加内存消耗。
- 实现模型时常见的错误来源,特别是分布式训练。
- 由于精度问题,难以在不同的硬件上复现训练结果。
目前,很多研究开始寻找替代BatchNorm的归一化层,但这些替代层要么表现不行,要么会带来新的问题,比如增加推理的计算消耗。而另外一些研究则尝试去掉归一化层,比如初始化残差分支的权值,使其输出为零,保证训练初期大部分的信息通过skip path进行传递。虽然能够训练很深的网络,但使用简单的初始化方法的网络的准确率较差,而且这样的初始化很难用于更复杂的网络中。
因此,论文希望找出一种有效地训练不含BatchNorm的深度残差网络的方法,而且测试集性能能够媲美当前的SOTA,论文主要贡献如下:
- 提出信号传播图(Signal Propagation Plots, SPPs),可辅助观察初始阶段的推理信号传播情况,确定如何设计无BatchNorm的ResNet来达到类似的信号传播效果。
- 验证发现无BatchNorm的ResNet效果不好的关键在于非线性激活(ReLU)的使用,经过非线性激活的输出的均值总是正数,导致权值的均值随着网络深度的增加而急剧增加。于是提出Scaled Weight Standardization,能够阻止信号均值的增长,大幅提升性能。
- 对ResNet进行normalization-free改造以及添加Scaled Weight Standardization训练,在ImageNet上与原版的ResNet有相当的性能,层数达到288层。
- 对RegNet进行normalization-free改造,结合EfficientNet的混合缩放,构造了NF-RegNet系列,在不同的计算量上都达到与EfficientNet相当的性能。
Signal Propagation Plots
许多研究从理论上分析ResNet的信号传播,却很少会在设计或魔改网络的时候实地验证不同层数的特征缩放情况。实际上,用任意输入进行前向推理,然后记录网络不同位置特征的统计信息,可以很直观地了解信息传播状况并尽快发现隐藏的问题,不用经历漫长的失败训练。于是,论文提出了信号传播图(Signal Propagation Plots,SPPs),输入随机高斯输入或真实训练样本,然后分别统计每个残差block输出的以下信息:
- Average Channel Squared Mean,在NHW维计算均值的平方(平衡正负均值),然后在C维计算平均值,越接近零是越好的。
- Average Channel Variance,在NHW维计算方差,然后在C维计算平均值,用于衡量信号的幅度,可以看到信号是爆炸抑或是衰减。
- Residual Average Channel Variance,仅计算残差分支输出,用于评估分支是否被正确初始化。
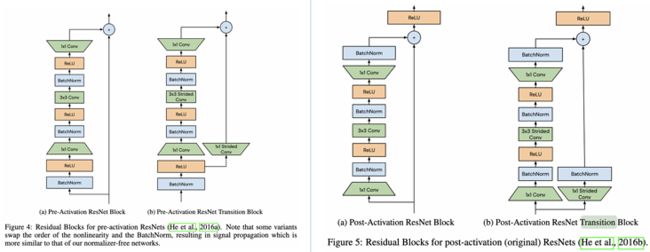
论文对常见的BN-ReLU-Conv结构和不常见的ReLU-BN-Conv结构进行了实验统计,实验的网络为600层ResNet,采用He初始化,定义residual block为$x_{l+1}=f_{l}(x_{l}) + x_{l}$,从SPPs可以发现了以下现象:
- Average Channel Variance随着网络深度线性增长,然后在transition block处重置为较低值。这是由于在训练初始阶段,residual block的输出的方差为$Var(x_{l+1})=Var(f_{l}(x_{l})) + Var(x_{l})$,不断累积residual branch和skip path的方差。而在transition block处,skip path的输入被BatchNorm处理过,所以block的输出的方差直接被重置了。
- BN-ReLU-Conv的Average Squared Channel Means也是随着网络深度不断增加,虽然BatchNorm的输出是零均值的,但经过ReLU之后就变成了正均值,再与skip path相加就不断地增加直到transition block的出现,这种现象可称为mean-shift。
- BN-ReLU的Residual Average Channel Variance大约为0.68,ReLU-BN的则大约为1。BN-ReLU的方差变小主要由于ReLU,后面会分析到,但理论应该是0.34左右,而且这里每个transition block的残差分支输出却为1,有点奇怪,如果知道的读者麻烦评论或私信一下。
假如直接去掉BatchNorm,Average Squared Channel Means和Average Channel Variance将会不断地增加,这也是深层网络难以训练的原因。所以要去掉BatchNorm,必须设法模拟BatchNorm的信号传递效果。
Normalizer-Free ResNets(NF-ResNets)
根据前面的SPPs,论文设计了新的redsidual block$x_{l+1}=x_l+\alpha f_l(x_l/\beta_l)$,主要模拟BatchNorm在均值和方差上的表现,具体如下:
- $f(\cdot)$为residual branch的计算函数,该函数需要特殊初始化,保证初期具有保持方差的功能,即$Var(f_l(z))=Var(z)$,这样的约束能够帮助更好地解释和分析网络的信号增长。
- $\beta_l=\sqrt{Var(x_l)}$为固定标量,值为输入特征的标准差,保证$f_l(\cdot)$为单位方差。
- $\alpha$为超参数,用于控制block间的方差增长速度。
根据上面的设计,给定$Var(x_0)=1$和$\beta_l=\sqrt{Var(x_l)}$,可根据$Var(x_l)=Var(x_{l-1})+\alpha^2$直接计算第$l$个residual block的输出的方差。为了模拟ResNet中的累积方差在transition block处被重置,需要将transition block的skip path的输入缩小为$x_l/\beta_l$,保证每个stage开头的transition block输出方差满足$Var(x_{l+1})=1+\alpha^2$。将上述简单缩放策略应用到残差网络并去掉BatchNorm层,就得到了Normalizer-Free ResNets(NF-ResNets)。
ReLU Activations Induce Mean Shifts
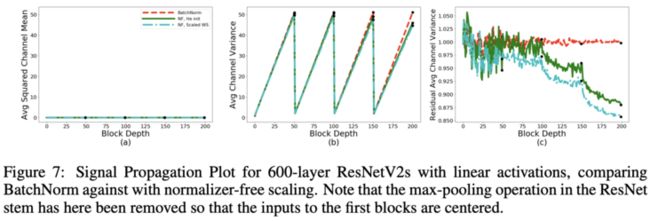
论文对使用He初始化的NF-ResNet进行SPPs分析,结果如图2,发现了两个比较意外的现象:
- Average Channel Squared Mean随着网络变深不断增加,值大到超过了方差,有mean-shift现象。
- 跟BN-ReLU-Conv类似,残差分支输出的方差始终小于1。
为了验证上述现象,论文将网络的ReLU去掉再进行SPPs分析。如图7所示,当去掉ReLU后,Average Channel Squared Mean接近于0,而且残差分支输出的接近1,这表明是ReLU导致了mean-shift现象。
论文也从理论的角度分析了这一现象,首先定义转化$z=Wg(x)$,$W$为任意且固定的矩阵,$g(\cdot)$为作用于独立同分布输入$x$上的elememt-wise激活函数,所以$g(x)$也是独立同分布的。假设每个维度$i$都有$\mathbb{E}(g(x_i))=\mu_g$以及$Var(g(x_i))=\sigma^2_g$,则输出$z_i=\sum^N_jW_{i,j}g(x_j)$的均值和方差为:
其中,$\mu w_{i,.}$和$\sigma w_{i,.}$为$W$的$i$行(fan-in)的均值和方差:
当$g(\cdot)$为ReLU激活函数时,则$g(x)\ge 0$,意味着后续的线性层的输入都为正均值。如果$x_i\sim\mathcal{N}(0,1)$,则$\mu_g=1/\sqrt{2\pi}$。由于$\mu_g>0$,如果$\mu w_i$也是非零,则$z_i$同样有非零均值。需要注意的是,即使$W$从均值为零的分布中采样而来,其实际的矩阵均值肯定不会为零,所以残差分支的任意维度的输出也不会为零,随着网络深度的增加,越来越难训练。
Scaled Weight Standardization
为了消除mean-shift现象以及保证残差分支$f_l(\cdot)$具有方差不变的特性,论文借鉴了Weight Standardization和Centered Weight Standardization,提出Scaled Weight Standardization(Scaled WS)方法,该方法对卷积层的权值重新进行如下的初始化:
$\mu$和$\sigma$为卷积核的fan-in的均值和方差,权值$W$初始为高斯权值,$\gamma$为固定常量。代入公式1可以得出,对于$z=\hat{W}g(x)$,有$\mathbb{E}(z_i)=0$,去除了mean-shift现象。另外,方差变为$Var(z_i)=\gamma^2\sigma^2_g$,$\gamma$值由使用的激活函数决定,可保持方差不变。
Scaled WS训练时增加的开销很少,而且与batch数据无关,在推理的时候更是无额外开销的。另外,训练和测试时的计算逻辑保持一致,对分布式训练也很友好。从图2的SPPs曲线可以看出,加入Scaled WS的NF-ResNet-600的表现跟ReLU-BN-Conv十分相似。
Determining Nonlinerity-Specific Constants
最后的因素是$\gamma$值的确定,保证残差分支输出的方差在初始阶段接近1。$\gamma$值由网络使用的非线性激活类型决定,假设非线性的输入$x\sim\mathcal{N}(0,1)$,则ReLU输出$g(x)=max(x,0)$相当于从方差为$\sigma^2_g=(1/2)(1-(1/\pi))$的高斯分布采样而来。由于$Var(\hat{W}g(x))=\gamma^2\sigma^2_g$,可设置$\gamma=1/\sigma_g=\frac{\sqrt{2}}{\sqrt{1-\frac{1}{\pi}}}$来保证$Var(\hat{W}g(x))=1$。虽然真实的输入不是完全符合$x\sim \mathcal{N}(0,1)$,在实践中上述的$\gamma$设定依然有不错的表现。
对于其他复杂的非线性激活,如SiLU和Swish,公式推导会涉及复杂的积分,甚至推出不出来。在这种情况下,可使用数值近似的方法。先从高斯分布中采样多个$N$维向量$x$,计算每个向量的激活输出的实际方差$Var(g(x))$,再取实际方差均值的平方根即可。
Other Building Block and Relaxed Constraints
本文的核心在于保持正确的信息传递,所以许多常见的网络结构都要进行修改。如同选择$\gamma$值一样,可通过分析或实践判断必要的修改。比如SE模块$y=sigmoid(MLP(pool(h)))*h$,输出需要与$[0,1]$的权值进行相乘,导致信息传递减弱,网络变得不稳定。使用上面提到的数值近似进行单独分析,发现期望方差为0.5,这意味着输出需要乘以2来恢复正确的信息传递。
实际上,有时相对简单的网络结构修改就可以保持很好的信息传递,而有时候即便网络结构不修改,网络本身也能够对网络结构导致的信息衰减有很好的鲁棒性。因此,论文也尝试在维持稳定训练的前提下,测试Scaled WS层的约束的最大放松程度。比如,为Scaled WS层恢复一些卷积的表达能力,加入可学习的缩放因子和偏置,分别用于权值相乘和非线性输出相加。当这些可学习参数没有任何约束时,训练的稳定性没有受到很大的影响,反而对大于150层的网络训练有一定的帮助。所以,NF-ResNet直接放松了约束,加入两个可学习参数。
论文的附录有详细的网络实现细节,有兴趣的可以去看看。
Summary
总结一下,Normalizer-Free ResNet的核心有以下几点:
- 计算前向传播的期望方差$\beta^2_l$,每经过一个残差block稳定增加$\alpha^2$,残差分支的输入需要缩小$\beta_l$倍。
- 将transition block中skip path的卷积输入缩小$\beta_l$倍,并在transition block后将方差重置为$\beta_{l+1}=1+\alpha^2$。
- 对所有的卷积层使用Scaled Weight Standardization初始化,基于$x\sim\mathcal{N}(0,1)$计算激活函数$g(x)$对应的$\gamma$值,为激活函数输出的期望标准差的倒数$\frac{1}{\sqrt{Var(g(x))}}$。
Experiments
对比RegNet的Normalizer-Free变种与其他方法的对比,相对于EfficientNet还是差点,但已经十分接近了。
Conclusion
论文提出NF-ResNet,根据网络的实际信号传递进行分析,模拟BatchNorm在均值和方差传递上的表现,进而代替BatchNorm。论文实验和分析十分足,出来的效果也很不错。一些初始化方法的理论效果是对的,但实际使用会有偏差,论文通过实践分析发现了这一点进行补充,贯彻了实践出真知的道理。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】