小波变换db4进行四层分解及其信号重构—matlab分析及C语言实现
小波变换db4进行四层分解及其信号重构
- 前言
- 一、Matlab中小波变换的相关函数
-
- 1. wavedec函数
- 2. wrcoef函数
- 二、C语言实现小波分解与重构
-
- 1. 信号分解
- 2. 信号重构
- 三、结果比较
-
- 1. 信号分解与wavedec函数
- 2. 信号重构与wrcoef函数
- 总结
- 参考文章
前言
本篇文章主要分析了matlab中关于小波变换的相关函数:wavedec(用于小波分解)和wrcoef(用于小波重构)。通过分析两个函数的实际动作,进一步用C语言实现小波变换的分解及重构。最后比较了matlab的结果与C语言的结果,结果一致,实现了C语言的小波变换。
(*ps:本文只针对db4小波,分析四层的小波变换。其他小波及不同层数的分解需要根据实际情况对程序进行改动。)
一、Matlab中小波变换的相关函数
1. wavedec函数
wavedec函数是用于小波分解的函数,在matlab中使用时的基本格式如下:
[C,L] = wavedec(rawData,4,'db4');
输入:
名称
意义
rawData
需要分解的原始数据
4
分解的层数
‘db4’
使用的小波信号
这里用于测试的原始数据为:
rawData = [24,34,49,48,25,17,34,50,64,71,64,54,53,55,56,60];
输出:
名称
意义
C
分解出的各层细节分量cD与最后一层的近似分量cA
L
与C中对应的cA与cD的数量
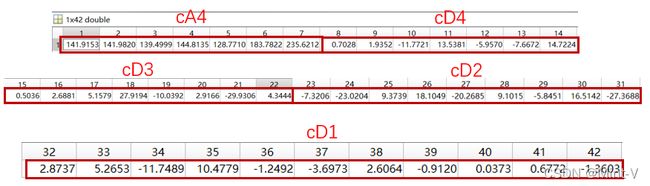
C和L的具体含义在matlab中解释如下:

上图为进行三层分解的结果示意图。因此在对原始数据进行四层分解时,C中的数据应为:cA4 cD4 cD3 cD2 cD1。而L中的结果就是每个数据的长度。
下面对wavedec函数中的实际动作进行分析:
通过在matlab中查看该函数的代码可以发现,wavedec函数最核心的内容其实就是离散小波变换(dwt):
[x,d] = dwt(x,Lo_D,Hi_D);
这里出现了Lo_D和Hi_D两个量,x是输入的原始数据,那么Lo_D和Hi_D分别是什么?再深入查看代码,可以发现这两个量其实是每个小波信号都有的低通分解量和高通分解量。不同的小波信号,其分解量也不同,但每个小波信号的分解量值是固定不变的。可以在matlab中通过wfilters函数获取各个小波信号的分解量,获取’db4’小波的分解量如下:
[Lo_D,Hi_D,Lo_R,Hi_R]=wfilters('db4');
这时又引出了两个量:Lo_R(低通重构)和Hi_R(高通重构),和上面的分解量对应,这两个量用于信号的重构,在wrcoef函数中会使用到。
得出的结果:
Lo_D =[ -0.0106,0.0329,0.0308,-0.1870,-0.0280,0.6309,0.7148,0.2304];
Hi_D =[-0.2304,0.7148,-0.6309,-0.0280,0.1870,0.0308,-0.0329,-0.0106];
Lo_R =[0.2304,0.7148,0.6309,-0.0280,-0.1870,0.0308,0.0329,-0.0106];
Hi_R =[-0.0106,-0.0329,0.0308,0.1870,-0.0280,-0.6309,0.7148,-0.2304];
到这里,分析wavedec函数就变成了分析dwt函数。
matlab中对dwt函数的结构可以用以下的图进行简单解释:

从图中可以看出,实现离散小波变换,首先将原始信号分别通过低通滤波器和高通滤波器,然后分别进行降采样就可得到cA与cD。这里的“通过低通滤波器和高通滤波器”可以简单的理解为信号与之前求得的两个分解量(Lo_D和Hi_D)进行卷积,具体的含义可参考:小波学习之一(单层一维离散小波变换DWT的Mallat算法C++和MATLAB实现) —转载。
这篇文章对单层一维离散小波变换的分解进行了十分详细的解释,并且使用C++进行了小波的分解与重构,能够实现信号的重构,但是其信号分解的结果与matlab的结果存在出入。此外,在实现单层的小波分解与重构的基础上,我们的目标是实现多层信号的分解与重构。因此在这篇文章代码的基础上,笔者对其进行了更改,在改变成C语言版本的同时实现了信号的多层分解与重构,使其结果与matlab结果保持一致。
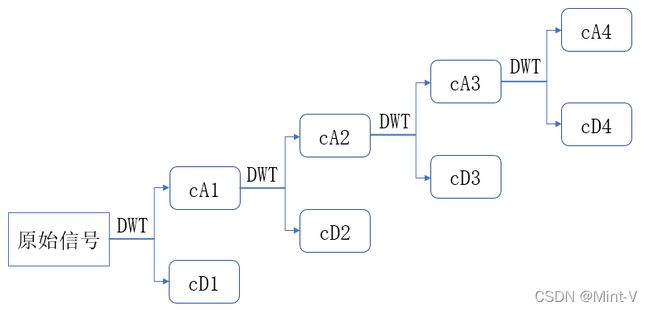
在小波分解中,对信号的分解是一层一层进行的,对每一层的近似分量进行分解以获得下一层的近似分量与细节分量,其原理如下图所示。因此,要实现wavedec函数功能就要对每一层进行离散小波变换(dwt)。
对原始信号进行离散小波变换(dwt)后,依次对得到的近似分量(cA)进行离散小波变换以获得下一层的分解量。将每一层需要的cD与cA及其个数汇总起来就可得出wavedec函数的结果C和L。
2. wrcoef函数
wrcoef函数用于对分解后的信号进行重构,在matlab中的使用方法如下:
[d1] = wrcoef('d',C,L,'db4',1);
[d2] = wrcoef('d',C,L,'db4',2);
[d3] = wrcoef('d',C,L,'db4',3);
[d4] = wrcoef('d',C,L,'db4',4);
[a4] = wrcoef('a',C,L,'db4',4);
输入:
名称
意义
‘d’ / ‘a’
对细节分量(cD)重构 / 对近似分量(cA)重构
C
从wavedec得到的结果,包括近似分量和细节分量
L
从wavedec得到的结果,近似分量和细节分量的数量
‘db4’
使用的小波信号
1/2/3/4
第1/2/3/4层的信号
输出:
名称
意义
d1
第一层分解出的细节分量cD1
d2
第二层分解出的细节分量cD2
d3
第三层分解出的细节分量cD3
d4
第四层分解出的细节分量cD4
a4
第四层分解出的近似分量cA4
wrcoef函数的内部实际动作可大致分为三步:
升采样——卷积——截取数据使之与原信号长度相同
- 升采样
单纯使用分解后的数据进行重构时,无法恢复到原有的长度,因此需要先进行升采样。这里的升采样本质上是插值补零。
(举一个栗子)
原始数据:1,2,3,4,5,6
升采样后:0,1,0,2,0,3,0,4,0,5,0,6 - 卷积
将要重构的数据与之前提到的两个重构量Lo_R(低通重构)和Hi_R(高通重构)进行卷积。
!这里有个非常关键的点!
从上面给出的小波分解的原理图可以看出,除了第一层的cA与cD是由原始数据直接分解得到之外,之后每一层的cA和cD都是由上一层的cA分解出来的,因此在信号重构时要注意:与分解后的信号相卷积的另一个量是什么。这个量只有两个选择:Lo_R或者Hi_R。分解后的信号属于细节分量时,要与Hi_R进行卷积;分解后的信号属于近似分量时,要与Lo_R卷积。
文字描述不太清晰,下面用示例来表示:
%示例1:重构d3信号至原始数据长度
d3由第二层的cA2分解而来,而d3本身属于细节分量,则d3先与Hi_R进行卷积,进而重构得出cA2;
cA2由第一层的cA1分解而来,而cA2本身属于近似分量,则cA2与Lo_R进行卷积,进而重构得出cA1;
cA1由原始数据分解而来,而cA1本身属于近似分量,则cA1与Lo_R进行卷积,进而重构得出最终结果;
%示例2:重构a4信号至原始数据长度
a4由第三层的cA3分解而来,而a4本身属于近似分量,则a4先与Lo_R进行卷积,进而重构得出cA3;
cA3由第二层的cA2分解而来,而cA3本身属于近似分量,则cA3与Lo_R进行卷积,进而重构得出cA2;
cA2由第一层的cA1分解而来,而cA2本身属于近似分量,则cA2与Lo_R进行卷积,进而重构得出cA1;
cA1由原始数据分解而来,而cA1本身属于近似分量,则cA1与Lo_R进行卷积,进而重构得出最终结果;
其他信号的重构类似以上两个示例。
- 截取数据使之与原信号长度相同
卷积后的结果长度会大于原始信号的长度,因此需要对重构出的结果进行截取。针对’db4’小波,从卷积结果的第8个数据进行截取,一直截取到与上一层的近似分量cA相同长度的数据,然后一层一层向上递推,最终得到与原始数据相同的长度。(如果换成其他的‘dbn’小波,从第2n个数据开始截取)
二、C语言实现小波分解与重构
1. 信号分解
信号分解如上所述,是对原始信号或每一层的近似分量(cA)进行离散小波变换(dwt),以获得下一层的近似分量与细节分量。因此C语言实现信号分解如下:
(需要注意的是,这里的原始数据rawdata最好不要超过512个,否则容易出错。当原始数据多于512个时,需要改变WaveletDB4函数中各个cA和cD的数组大小。)
double cA[300], cD[300], cA1[150], cD1[150];
double cA2[100], cD2[100], cA3[50], cD3[50];
#include
#include
#include
double rawdata[16] = { 24,34,49,48,25,17,34,50,64,71,64,54,53,55,56,60 };
double db4_Lo_D[8] = { -0.0105974017850690, 0.0328830116668852, 0.0308413818355607, -0.1870348117190931, -0.0279837694168599, 0.6308807679398587, 0.7148465705529154, 0.2303778133088964 };
double db4_Hi_D[8] = { -0.2303778133088964, 0.7148465705529154, -0.6308807679398587, -0.0279837694168599, 0.1870348117190931, 0.0308413818355607, -0.0328830116668852, -0.0105974017850690 };
void WaveletDwt(double sourceData[], int dataLen, double *cA, double *cD) // rawData, the length of rawData , cA, cD
{
int filterLen = 8; // 滤波器的长度
int n, k, p;
int decLen = (dataLen + filterLen - 1) / 2;
double tmp = 0;
for (n = 0; n < decLen; n++)
{
cA[n] = 0;
cD[n] = 0;
for (k = 0; k < filterLen; k++)
{
p = 2 * n - k + 1;
if ((p < 0) && (p >= -filterLen + 1))
tmp = sourceData[-p - 1];
else if ((p > dataLen - 1) && (p <= dataLen + filterLen - 2))
tmp = sourceData[2 * dataLen - p - 1];
else if ((p >= 0) && (p < dataLen - 1 + 1))
tmp = sourceData[p];
else
tmp = 0;
cA[n] += db4_Lo_D[k] * tmp; // cA
cD[n] += db4_Hi_D[k] * tmp; // cD
}
}
return;
}
void WaveletDB4(double sourceData[], int dataLen, double *C, int *L)
{
double cA[300], cD[300], cA1[150], cD1[150];
double cA2[100], cD2[100], cA3[50], cD3[50];
L[0] = dataLen;
int i;
WaveletDwt(sourceData, dataLen, cA, cD); //One-layer decomposition
L[1] = (dataLen + 7) / 2;
for (i = 0; i < L[1]; i++)
{
C[i] = cD[i];
}
WaveletDwt(cA, L[1], cA1, cD1); //Two-layer decomposition
L[2] = (L[1] + 7) / 2;
for (i = L[1]; i < L[1] + L[2]; i++)
{
C[i] = cD1[i - L[1]];
}
WaveletDwt(cA1, L[2], cA2, cD2); //Three-layer decomposition
L[3] = (L[2] + 7) / 2;
for (i = L[1] + L[2]; i < L[1] + L[2] + L[3]; i++)
{
C[i] = cD2[i - L[1] - L[2]];
}
WaveletDwt(cA2, L[3], cA3, cD3); //Four-layer decomposition
L[4] = (L[3] + 7) / 2;
for (i = L[1] + L[2] + L[3]; i < L[1] + L[2] + L[3] + L[4]; i++)
{
C[i] = cD3[i - L[1] - L[2] - L[3]];
}
L[5] = (L[3] + 7) / 2;
for (i = L[1] + L[2] + L[3] + L[4]; i < L[1] + L[2] + L[3] + L[4] + L[5]; i++)
{
C[i] = cA3[i - L[1] - L[2] - L[3] - L[4]];
}
return;
}
//=========================================end of WaveletDB4===============================================//
int main() {
int L[6];
double C[600];
int DataLen = sizeof(rawdata) / sizeof(double);
WaveletDB4(rawdata, DataLen, C, L); //C: CD1 CD2 CD3 CD4 CA4 L: (length of) raw data, CD1, CD2, CD3, CD4, CA4
for(int i = 0; i < (L[1]+L[2]+L[3]+L[4]+L[5]); i++)
{
printf("C[");printf("%d",i);printf("]:");
printf("%f
", C[i]);
}
for (int i = 0; i < 6; i++)
{
printf("L["); printf("%d", i); printf("]:");
printf("%d
", L[i]);
}
}
2. 信号重构
信号重构的本质是对需要重构的信号进行单支重构(升采样—卷积—截取)。这里的单支重构与普通的小波逆变换原理一样,只是省去“将高低频部分相加在一起”这一步,详见wrcoef函数的实际动作这篇文章。通过不断对信号单支重构至上一层信号,直至重构成与原始信号同等长度,形成最终结果。因此C语言实现信号重构如下:
double db4_Lo_R[8] = { 0.2303778133088964, 0.7148465705529154, 0.6308807679398587, -0.0279837694168599, -0.1870348117190931, 0.0308413818355607, 0.0328830116668852, -0.0105974017850690 };
double db4_Hi_R[8] = { -0.0105974017850690, -0.0328830116668852, 0.0308413818355607, 0.1870348117190931, -0.0279837694168599, -0.6308807679398587, 0.7148465705529154, -0.2303778133088964 };
void WaveletIdwt_CD(double cD[], int cALength, double *recData, int recLength)
{
int filterLen = 8;
int recLen = recLength;
int num = cALength * 2;
double *temp = (double *)malloc(num * sizeof(double));
int k = 0;
// Upsampling
for (int n = 0; n < num; n++)
{
if (n % 2 == 0)
{
temp[n] = 0;
}
else
{
temp[n] = cD[k];
k++;
}
}
int num_conv = cALength * 2 + 8 - 1;
double *xx = (double *)malloc(num_conv * sizeof(double));
// Initialization
for (int i = 0; i < num_conv; i++) {
xx[i] = 0;
}
// Convolution
for (int i = 0; i < 8; i++) {
for (int j = 0; j < cALength * 2; j++) {
xx[i + j] += temp[j] * db4_Hi_R[i];
}
}
// Results
for (int i = 7; i < recLen + 7; i++) {
recData[i - 7] = xx[i];
}
free(temp);
free(xx);
return;
}
void WaveletIdwt_CA(double *cA, int cALength, double *recData, int recLength)
{
int filterLen = 8;
int recLen = recLength;
int num = cALength * 2;
double *temp = (double *)malloc(num * sizeof(double));
int k = 0;
// Upsampling
for (int n = 0; n < num; n++)
{
if (n % 2 == 0)
{
temp[n] = 0;
}
else
{
temp[n] = cA[k];
k++;
}
}
int num_conv = cALength * 2 + 8 - 1;
double *xx = (double *)malloc(num_conv * sizeof(double));
// Initialization
for (int i = 0; i < num_conv; i++) {
xx[i] = 0;
}
// Convolution
for (int i = 0; i < 8; i++) {
for (int j = 0; j < cALength * 2; j++) {
xx[i + j] += temp[j] * db4_Lo_R[i];
}
}
// Results
for (int i = 7; i < recLen + 7; i++) {
recData[i - 7] = xx[i];
}
free(temp);
free(xx);
return;
}
//============================================end of Single branch reconstruction===================================//
void getcD1(double *C, int *L, double *cD1) {
int recLen = L[0];
int num = L[1];
double *cD = (double *)malloc(num * sizeof(double));
for (int i = 0; i < num; i++) {
cD[i] = C[i];
}
WaveletIdwt_CD(cD, num, cD1, recLen);
free(cD);
return;
}
void getcD2(double *C, int *L, double *cD2)
{
int recLen = L[0];
int num_cd1 = L[1];
int num_cd2 = L[2];
double *cD = (double *)malloc(num_cd2 * sizeof(double));
double *rec1 = (double *)malloc(num_cd1 * sizeof(double));
for (int i = num_cd1; i < num_cd1 + num_cd2; i++) {
cD[i - num_cd1] = C[i];
}
WaveletIdwt_CD(cD, num_cd2, rec1, num_cd1);
WaveletIdwt_CA(rec1, num_cd1, cD2, recLen);
free(cD);
free(rec1);
return;
}
void getcD3(double *C, int *L, double *cD3)
{
int recLen = L[0];
int num_cd1 = L[1];
int num_cd2 = L[2];
int num_cd3 = L[3];
double *cD = (double *)malloc(num_cd3 * sizeof(double));
double *rec1 = (double *)malloc(num_cd2 * sizeof(double));
double *rec2 = (double *)malloc(num_cd1 * sizeof(double));
for (int i = num_cd1 + num_cd2; i < num_cd1 + num_cd2 + num_cd3; i++) {
cD[i - num_cd1 - num_cd2] = C[i];
}
WaveletIdwt_CD(cD, num_cd3, rec1, num_cd2);
WaveletIdwt_CA(rec1, num_cd2, rec2, num_cd1);
WaveletIdwt_CA(rec2, num_cd1, cD3, recLen);
free(cD);
free(rec1);
free(rec2);
return;
}
void getcD4(double *C, int *L, double *cD4)
{
int recLen = L[0];
int num_cd1 = L[1];
int num_cd2 = L[2];
int num_cd3 = L[3];
int num_cd4 = L[4];
double *cD = (double *)malloc(num_cd4 * sizeof(double));
double *rec1 = (double *)malloc(num_cd3 * sizeof(double));
double *rec2 = (double *)malloc(num_cd2 * sizeof(double));
double *rec3 = (double *)malloc(num_cd1 * sizeof(double));
for (int i = num_cd1 + num_cd2 + num_cd3; i < num_cd1 + num_cd2 + num_cd3 + num_cd4; i++) {
cD[i - num_cd1 - num_cd2 - num_cd3] = C[i];
}
WaveletIdwt_CD(cD, num_cd4, rec1, num_cd3);
WaveletIdwt_CA(rec1, num_cd3, rec2, num_cd2);
WaveletIdwt_CA(rec2, num_cd2, rec3, num_cd1);
WaveletIdwt_CA(rec3, num_cd1, cD4, recLen);
free(cD);
free(rec1);
free(rec2);
free(rec3);
return;
}
void getcA4(double *C, int *L, double *cA4)
{
int recLen = L[0];
int num_cd1 = L[1];
int num_cd2 = L[2];
int num_cd3 = L[3];
int num_cd4 = L[4];
int num_ca4 = L[5];
double *cA = (double *)malloc(num_ca4 * sizeof(double));
double *rec1 = (double *)malloc(num_cd3 * sizeof(double));
double *rec2 = (double *)malloc(num_cd2 * sizeof(double));
double *rec3 = (double *)malloc(num_cd1 * sizeof(double));
for (int i = num_cd1 + num_cd2 + num_cd3 + num_cd4; i < num_cd1 + num_cd2 + num_cd3 + num_cd4 + num_ca4; i++) {
cA[i - num_cd1 - num_cd2 - num_cd3 - num_cd4] = C[i];
}
WaveletIdwt_CA(cA, num_ca4, rec1, num_cd3);
WaveletIdwt_CA(rec1, num_cd3, rec2, num_cd2);
WaveletIdwt_CA(rec2, num_cd2, rec3, num_cd1);
WaveletIdwt_CA(rec3, num_cd1, cA4, recLen);
free(cA);
free(rec1);
free(rec2);
free(rec3);
return;
}
int main() {
int L[6];
double C[600];
int DataLen = sizeof(rawdata) / sizeof(double);
double cD1[512];
double cD2[512];
double cD3[512];
double cD4[512];
double cA4[512];
WaveletDB4(rawdata, DataLen, C, L); //C: CD1 CD2 CD3 CD4 CA4 L: (length of) raw data, CD1, CD2, CD3, CD4, CA4
getcD1(C, L, cD1);
getcD2(C, L, cD2);
getcD3(C, L, cD3);
getcD4(C, L, cD4);
getcA4(C, L, cA4);
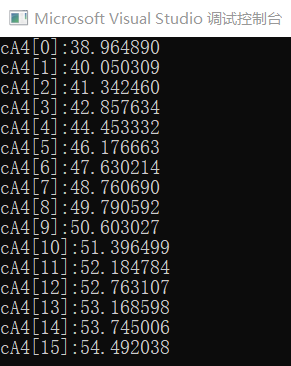
for (int i = 0; i < DataLen; i++) {
printf("cA4["); printf("%d", i); printf("]:");
printf("%f
", cA4[i]);
}
}
三、结果比较
1. 信号分解与wavedec函数
用C语言实现的信号分解结果如下:
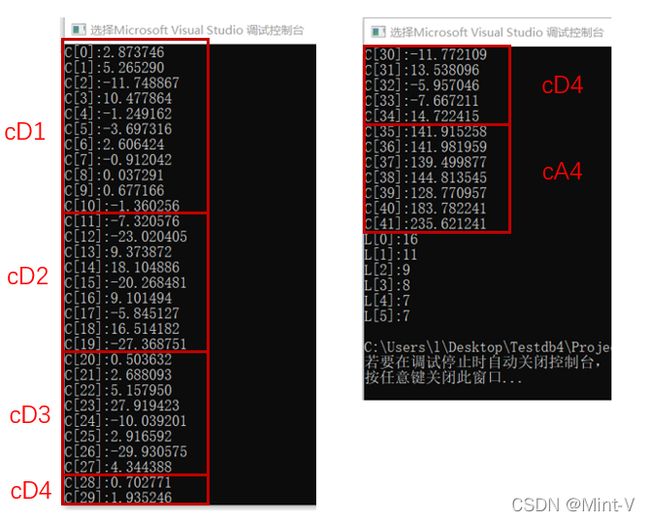
可以看出,这里C中各个量的大小与L中是对应的(L[0]是原始数据的大小,与C对应的大小从L[1]开始),且与matlab求出的结果一致。
2. 信号重构与wrcoef函数
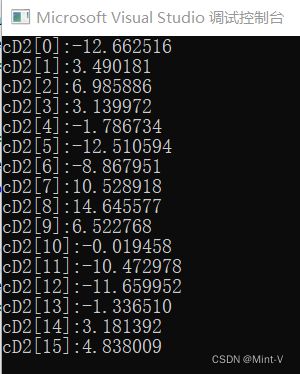
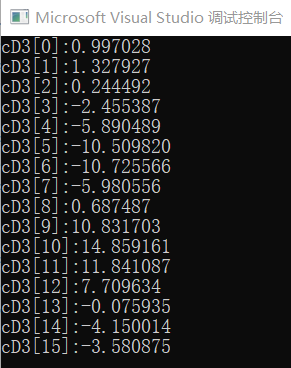
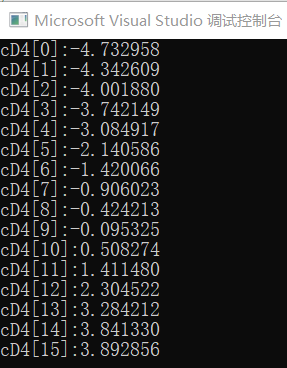
在matlab中运行wrcoef函数,同时运行C语言实现的信号重构,得出结果如下。
综上可以看出C语言实现了与matlab同样结果的信号重构。
总结
本篇文章通过C语言实现了’db4’小波的四层小波分解与重构,其结果与matlab结果能够保持一致,证明了其可行性。在理解了小波变换的分解与重构原理后,程序可扩展成其他的小波与不同的分解层数。
文章有理解不足或表述不清之处,见谅(′`)
参考文章
小波学习之一(单层一维离散小波变换DWT的Mallat算法C++和MATLAB实现) —转载
解析matlab函数wrcoef的内部实现
wrcoef函数的实际动作