【LeNet、AlexNet、VGG】

LeNet

  LeNet是最早用于图像处理的神经网络，主要是为了解决手写数字识别的问题，著名的数据集Minist就是伴随着LeNet的诞生而出现的。下面是其基本架构：

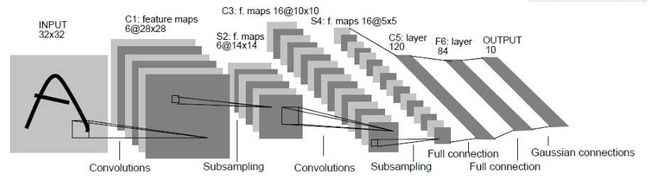
  其结构相对简单，其中的Pooling层可以使用MaxPooling，也可以使用AvgPooling，激活函数原始模型使用的是Sigmoid，不过也可以换成Relu，tanh等。

总结

• Lenet是是最早发布的卷积神经网络之一，因其在计算机视觉任务中的高效性能而受到广泛关注
• 先用卷积层来学习图片的空间信息，通过池化层降低图片的敏感度
• 然后使用全连接层来转换到类别空间，得到10类
• 两个卷积层再加一个多层感知机，最终得到从图片到类别的映射

代码实现

%matplotlib inline
import torch
from torch import nn
import torchvision
from torch.utils import data
from matplotlib import pyplot as plt
import numpy as np

trans = torchvision.transforms.ToTensor()

train_data = torchvision.datasets.FashionMNIST('../data/', train=True, download=False, transform=trans)

test_data = torchvision.datasets.FashionMNIST('../data/', train=False, download=False, transform=trans)

train_data.data.shape, test_data.data.shape

(torch.Size([60000, 28, 28]), torch.Size([10000, 28, 28]))

def get_dataloader(batch_size, train_data, test_data):
    train_dataloader = data.DataLoader(train_data, batch_size=batch_size, shuffle=True)
    test_dataloader = data.DataLoader(test_data, batch_size=batch_size, shuffle=False)
    return train_dataloader, test_dataloader

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        self.net = nn.Sequential(
            nn.Conv2d(1, 6, kernel_size=5, padding=2),
            nn.Sigmoid(),
            nn.MaxPool2d(kernel_size=2, stride=2),
            nn.Conv2d(6, 16, kernel_size=5),
            nn.Sigmoid(),
            nn.MaxPool2d(kernel_size=2, stride=2),
            nn.Flatten(),
            nn.Linear(16 * 5 * 5, 120),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            nn.Sigmoid(),
            nn.Linear(84, 10))
        
    def forward(self, x):
        x = x.view(-1, 1, 28, 28)
        return self.net(x)

def get_optimizer(model, lr):
    optimizer = torch.optim.SGD(model.parameters(), lr=lr)
    return optimizer

# 定义评判方法，对于分类问题，我们常使用准确率来判定
def accuracy(y_hat, y):
    padding = torch.argmax(y_hat, -1)
    right = (padding == y).sum().numpy()
    return right / y.shape[0]

def init_weights(m):
    if type(m) == nn.Linear or type(m) == nn.Conv2d:
        nn.init.xavier_uniform_(m.weight)

def train(epoches, batch_size, lr):
    model = LeNet()
    model.apply(init_weights)
    
    loss = nn.CrossEntropyLoss()
    optimizer = get_optimizer(model, lr)
    train_loader, test_loader = get_dataloader(batch_size, train_data, test_data)
    
    loss_lis = []
    train_acc_lis = []
    test_acc_lis = []
    
    for epoch in range(epoches):
        acc = 0
        l_sum = 0
        model.train()
        for X, y in train_loader:
            y_hat = model(X)
            l = loss(y_hat, y)
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            acc += accuracy(y_hat, y)
            l_sum += l.mean().detach().numpy()
        
        acc = acc / (train_data.data.shape[0] / batch_size)
        l_sum = l_sum / (train_data.data.shape[0] / batch_size)
        
        model.eval()
        acc_eval = 0
        for x, Y in test_loader:
            Y_hat = model(x)
            acc_eval += accuracy(Y_hat, Y)
        acc_eval /= (test_data.data.shape[0] / batch_size)
        
        loss_lis.append(l_sum)
        train_acc_lis.append(acc)
        test_acc_lis.append(acc_eval)
        
        print(f'epoch is {epoch + 1}, the loss is {l_sum} and the accuracy on train data is {acc}, on test data is{acc_eval}')
        
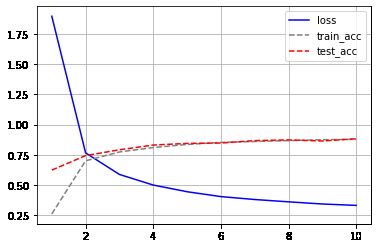
    plt.plot(np.arange(1, epoches + 1), loss_lis, color='blue', label='loss')
    plt.plot(np.arange(1, epoches + 1), train_acc_lis, color='grey', linestyle='--', label='train_acc')
    plt.plot(np.arange(1, epoches + 1), test_acc_lis, color='red', linestyle='--', label='test_acc')
    plt.grid()
    plt.legend(loc='upper right')
    plt.show()

train(10, 128, 0.9)

epoch is 1, the loss is 1.8979717952728272 and the accuracy on train data is 0.2590388888888889, on test data is0.6222
epoch is 2, the loss is 0.7648378531773885 and the accuracy on train data is 0.699338888888889, on test data is0.7426
epoch is 3, the loss is 0.5863379270553589 and the accuracy on train data is 0.7725944444444444, on test data is0.7907
epoch is 4, the loss is 0.4983555362065633 and the accuracy on train data is 0.8092, on test data is0.8301
epoch is 5, the loss is 0.4429962953249613 and the accuracy on train data is 0.8350277777777777, on test data is0.8435
epoch is 6, the loss is 0.4026765632947286 and the accuracy on train data is 0.8518888888888889, on test data is0.8468
epoch is 7, the loss is 0.37838911752700805 and the accuracy on train data is 0.8591833333333333, on test data is0.8668
epoch is 8, the loss is 0.35928820660909017 and the accuracy on train data is 0.8668888888888889, on test data is0.8727
epoch is 9, the loss is 0.34128332163492836 and the accuracy on train data is 0.8742888888888889, on test data is0.8638
epoch is 10, the loss is 0.32974659884770713 and the accuracy on train data is 0.8775555555555556, on test data is0.8824

AlexNet

   AlexNet诞生于2012年，与另一种观察图像特征的提取方法不同，它认为特征本身应该被学习，在合理的复杂性前提下，特征应该由多个共同学习的神经网络层组成，每个层都有可学习的参数。在机器视觉中，最底层可能检测边缘、颜色和纹理；更高层建立在底层表示的基础上，以表示更大的特征，更高层可以检测整个物体；最终的隐藏神经元可以学习图像的综合表示，从而使不同类别的数据易于区分

• AlexNet赢了2012年ImageNet竞赛
• 本质上是更深更大的LeNet
• 主要改进：
  • 丢弃法
  • ReLu
  • MaxPooling
• 计算机视觉方法论的改变（不再需要人工特征提取，而是让CNN去自己进行特征学习）
  
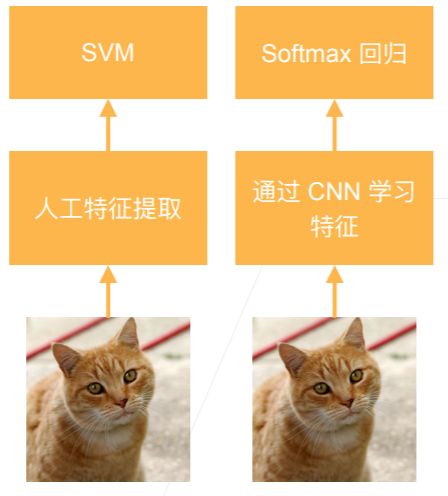
  AlexNet和LeNet的对比
  
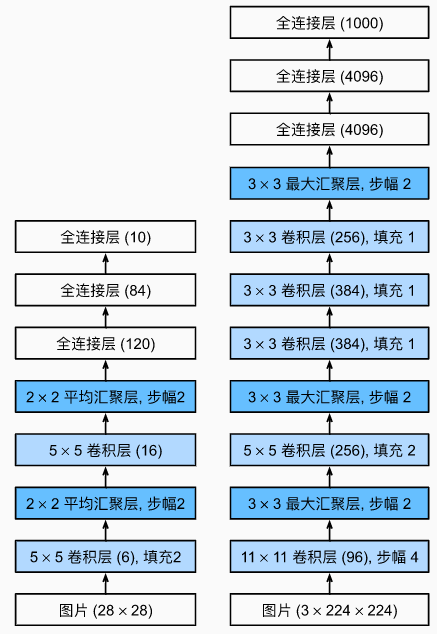
• AlexNet其实就是一个更大、更深的LeNet，由八层组成：5个卷积层、2个全连接隐藏层和一个全连接输出层
• AlexNet的输入是$224\times 224\times 3$的3通道RGB图片，LeNet的输入是$32\times 32\times 1$的单通道灰度图片
• 第一层：AlexNet使用了更大的核窗口（因为图片更大了，需要用更大的卷积窗口来捕获目标），通道数也更多了，从6变成了96（希望能够在第一层识别更多的模式，所以用了比较大的通道数），stride从2变成了4（这是由于当时GPU性能的限制，如果stride比较小的话，计算就会变得非常困难）
• 第二层：AlexNet使用了更大的池化层，stride都是2，因为LeNet的池化层窗口大小也是2，所以它每次看到的内容是不重叠的。$2\times 2$和$3\times 3$的主要区别是：
  • $2\times 2$允许一个像素往一边平移一点而不影响输出，$3\times 3$的话就允许一个像素左移或者右移都不影响输出；stride都等于2使得输出的高和宽都减半
• 第三层：AlexNet有一个padding为2的操作，它的作用就是使得输入和输出的大小是一样的；AlexNet的输出通道是256，使用了更多的输出通道来识别更多的模式
• ALexNet新加了3个卷积层
• AlexNet的全连接层也用了两个隐藏层，但是隐藏层更大（在最后一个卷积层后有两个全连接层，分别有4096个输出。 这两个巨大的全连接层拥有将近1GB的模型参数。 由于早期GPU显存有限，原版的AlexNet采用了双数据流设计，使得每个GPU只负责存储和计算模型的一半参数）
• Alex的激活函数从sigmoid变成了ReLu：
  • 1、ReLU激活函数的计算更简单，它不需要sigmoid激活函数那般复杂的求幂运算；
  • 2、当使用不同的参数初始化方法时，ReLU激活函数使训练模型更加容易；
  • 3、当sigmoid激活函数的输出非常接近于0或1时，这些区域的梯度几乎为0，因此反向传播无法继续更新一些模型参数，相反，ReLU激活函数在正区间的梯度总是1。 因此，如果模型参数没有正确初始化，sigmoid函数可能在正区间内得到几乎为0的梯度，从而使模型无法得到有效的训练。
    LeNet只使用了权重衰减，而AlexNet在全连接层的两个隐藏层之后加入了丢弃层（dropout、暂退法），来做模型的正则化，控制全连接层的模型复杂度
• 为了进一步扩充数据，AlexNet还做了数据的增强：对样本图片进行随机截取、随机调节亮度、随即调节色温（因为卷积对位置、光照等比较敏感，所以在输入图片中增加大量的变种，来模拟预测物体形状或者颜色的变化；因为神经网络能够记住所有的数据，通过这种变换之后来降低神经网络的这种能力，因为每次变换之后的物体都是不一样的）

总结

• AlexNet是更大更深的LeNet，但是整个架构是一样的，AlexNet的参数个数比LeNet多了10倍，计算复杂度多了260倍
• AlexNet新加入了一些小技巧使得训练更加容易：丢弃法（dropout）、ReLu、最大池化层、数据增强
• AlexNet首次证明了学习到的特征可以超越手工设计的特征，以很大的优势赢下了2012年的ImageNet竞赛之后，标志着新一轮的神经网络热潮的开始
• 尽管今天AlexNet已经被更有效的架构所超越，但它是从浅层网络到深层网络的关键一步
• Dropout、ReLU和预处理是提升计算机视觉任务性能的其他关键步骤

VGG

   Alexnet虽然证明了深层神经网络是有效果的，但是它最大的问题是模型不规则，结构不是很清晰，没有提供一个通用的模板来指导后续的研究人员设计新的网络。如果模型想要变得更大、更深，则需要很好的设计思想，使得整个框架更加规则

如何使模型更大更深

• 更多的全连接层（缺点是全连接层很大的话会占用很多的内存）
• 更多的卷积层（AlexNet是先将LeNet的模型给扩大之后，再加了三个卷积层，不好实现对模型进一步的加大、加深；VGG的思想是先将卷积层组成小块，然后再将卷积层进行堆叠）
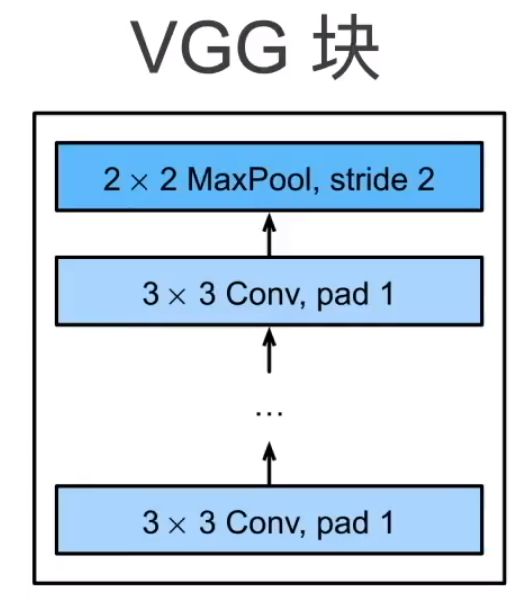
• 将卷积层组合成块（VGG提出了VGG块的概念，其实就是AlexNet思路的拓展：AlexNet中是三个一模一样的卷积层（$3\times 3$，384通道，padding等于1）加上一个池化层（$3\times 3$，最大池化层，stride=2）组成了一个小块：VGG块是在此基础上的拓展，它并不限制块中卷积层的层数和通道数），最大池化层重新用回了LeNet中的最大池化层窗口（$2\times 2$，最大池化层，stride=2）

VGG块

• VGG的核心思想是使用大量由一定数目的$3\times 3$的卷积层和一个最大池化层组成的VGG块进行堆叠，最终得到最后的网络

  • 为什么使用的卷积层是$3\times 3$，而不是$5\times 5$？
    • $5\times 5$的卷积层也用过，但是$5\times 5$的卷积层的计算量更大，所以层数就不会太大，VGG块就会变得浅一点，最终通过对比发现，在同样的计算开销之下，大量的$3\times 3$的卷积层堆叠起来比少量的$5\times 5$的卷积层堆叠起来的效果更好，也就是说模型更深、卷积窗口更小的情况下，效果会更好一点

• VGG块由两部分组成：多个填充为1的$3\times 3$卷积层（它有两个超参数：层数n、通道数m）和一个步幅为2的$2\times 2$最大池化层

VGG架构

• 其实就是使用多个VGG块进行堆叠来替换掉AlexNet中的卷积部分
  
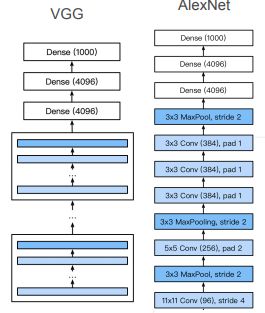
• VGG块重复的次数不同可以得到不同的架构，比如VGG-16、VGG-19，···
• 最后还是使用了两个4096的全连接层得到输出
• VGG对AlexNet最大的改进是：将AlexNet在LeNet的基础上新加的卷积层抽象出了VGG块，替换掉了AlexNet中原先并不规则的部分
• 类似于AlexNet、LeNet，VGG网络也可以分成两部分：第一部分主要由卷积层和汇聚层组成，第二部分由全连接层组成。从AlexNet到VGG，本质上都是块设计
• 原始的VGG网络有5个块，前2个块各有一个卷积层，后3个块个包含两个卷积层；第一个模块有64个输出通道，每个后续模块将输出通道的数量翻倍，直到达到512，由于该网络使用了8个卷积层和三个全连接层，因此通常被称为VGG-11（这里为什么是5块？因为原始输入图像的大小是224，每经过一个VGG块，输出的通道数会翻倍、高宽会减半，当减到第五次时输出的高宽为7，就不能再经过VGG块进行减半了）