最小生成树普里姆算法Prim
目录
前言
一、Prim算法的基本思路
二、代码实现
总结
前言
无论是什么程序都要和数据打交道,一个好的程序员会选择更优的数据结构来更好的解决问题,因此数据结构的重要性不言而喻。数据结构的学习本质上是让我们能见到很多前辈在解决一些要求时间和空间的难点问题上设计出的一系列解决方法,我们可以在今后借鉴这些方法,也可以根据这些方法在遇到具体的新问题时提出自己的解决方法。(所以各种定义等字眼就不用过度深究啦,每个人的表达方式不一样而已),在此以下的所有代码都是仅供参考,并不是唯一的答案,只要逻辑上能行的通,写出来的代码能达到相同的结果,并且在复杂度上差不多,就行了。
一、Prim算法的基本思路
Prim算法就要比Kruskal要简单很多,总的来说Prim算法就是将顶点分为两类:一类是在查找中就包含在生成树中的顶点,而剩下的就是另一类。
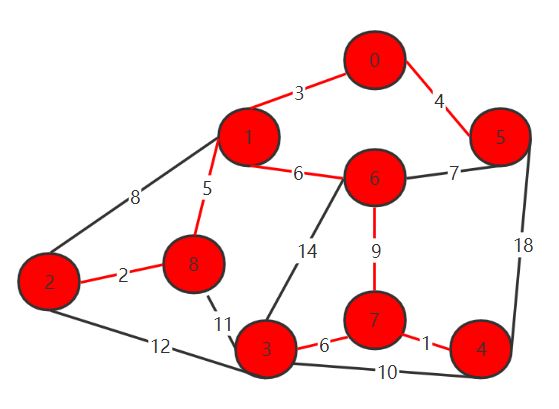
具体是什么意思呢,我们以这个带权图为例:
![]()
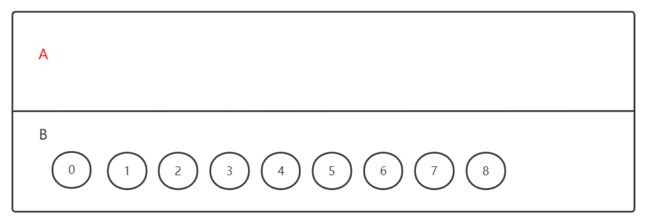
根据上文红字的描述,首先我们要先创建出两个类A、B,当然这里不是C++中的类,而是在逻辑上的一种抽象的概念;如下图所示:
在一开始图中所有的节点都在B类中,现在我们要找任意一个节点作为起始点放入A类中,然后持续地去找该节点的所有相邻点中权值最小的节点放入A类。
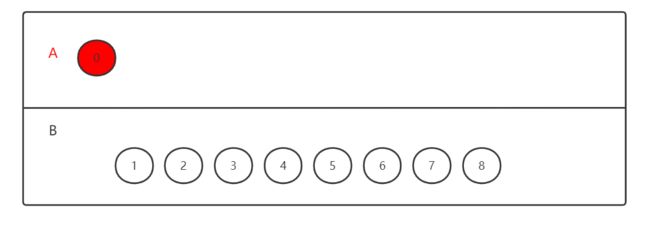
假定我们选择V0节点作为起始节点,①把V0放进A类中;②再找V0相邻的所有权值最小的点放进A类中,
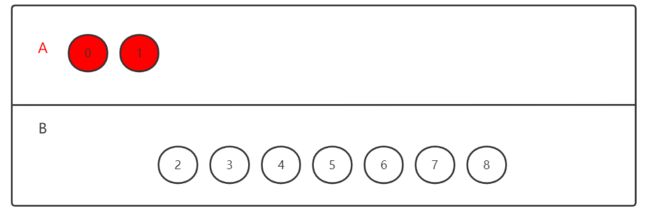
从带权图中我们可以得到与V0相邻的节点有V1和V5,而它们之间的边的权值分别是3和4,毫无疑问V1就是我们这一步要找的节点;
①
②
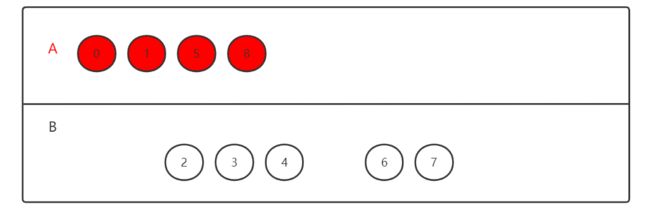
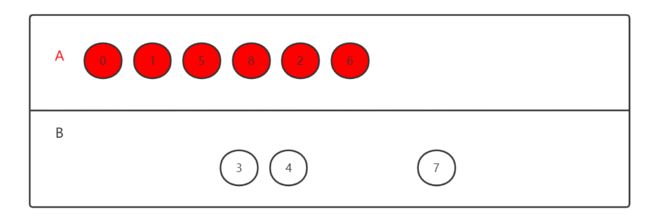
第③步,接着再找V0和V1所有相邻的点有V2 V8 V5 V6,同理可以得出V5为顶点的边权值最小,所以把V5放进A类中;
第④步再找V0 V1 V5所有相邻的点有V2 V8 V6 V4,V8是最小权值的边的顶点,放入V8;
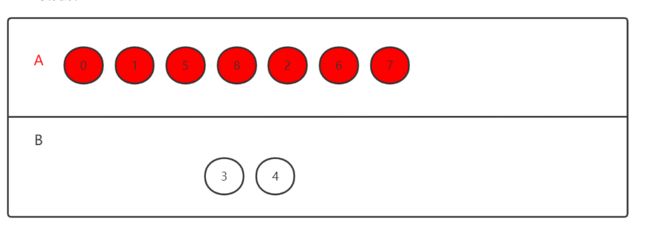
第⑤步再找V0 V1 V5 V8的所有邻接点V2 V3 V6 V4,同理放入V2;
第⑥步找V0 V1 V5 V8 V2的所有邻接点V3 V6 V4,放入V6;
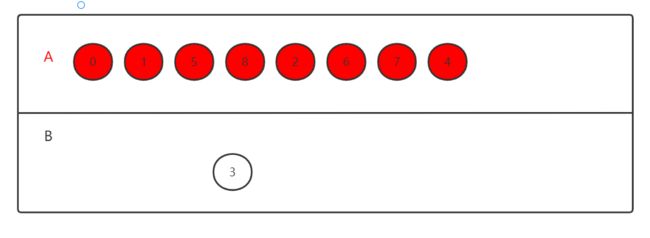
第⑦步重复上述的操作,先后放入V7 V4 V3。
③
④
⑤
⑥
⑦
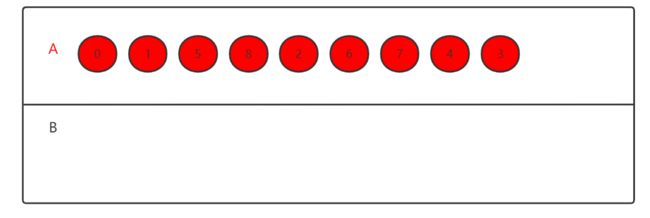
至此,所有的节点都放进了A类当中,回顾上述的这些操作,根据放入A类的节点的先后顺序,我在带权图上也标记了相对应的边,如下图所示,这些顶点和边就是我们要找的一个最小生成树;
把红色的部分单独拿出来,就是我们要找的其中一个最小生成树;
二、代码实现
理清了逻辑接下来就是代码实现。Prim在代码实现上相比于Kruskal来说也很简单,只需要按照上文的逻辑模拟就行了。
这里我还是用邻接矩阵去构建这么一个带权图,因为需要不断去访问边的权值;
void creategrahp(AdjMatrix* G)
{
int n, e;//n代表顶点数 e代表边数
int vi, vj;//vi vj代表边的两个顶点对
int w;//表示边的权值
printf("要输入的顶点数和边数\n");
scanf("%d%d",&n,&e);
G->numV = n;
G->numE = e;
//图的初始化
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if(i == j)
{
//一个非带权的图 0代表没有边 1代表有边
//边不指向自己 即对角线为0
G->Arc[i][j] = 0;
}
else
{
//如果是带权的图 初始化为0或者为一个不可能的值
G->Arc[i][j] = 65535;
}
}
}
//将顶点存入数组
for(int i = 0; i < G->numV; i++)
{
printf("请输入第%d个节点的信息\n",i + 1);
scanf("%d", &G->Vertices[i]);
}
//输入边的信息
for(int i = 0; i< G->numE; i++)
{
//如果输入的是顶点的值 需要从顶点集中查找对应的下标
//如果是带权图 还要输入权的信息
printf("请输入边的信息Vi,Vj和权值w\n");
scanf("%d%d%d",&vi,&vj,&w);
G->Arc[vi][vj] = w;
//如果是带权图 等于权值
//如果是有向图 就不对称
//如果是无向图 矩阵对称
G->Arc[vj][vi] = w;
}
}构建完的矩阵如下图所示(因为是无向图所以另一半只需要沿对角线镜像一下就行了,我比较懒,这里就不画全了)
接下来我们开辟两个数组adjvex和lowcast;其中adjvex是表示用来保存相关节点的下标的,也就是我们在上文中提到的A类;lowcast用来保存相关边的权值;这里我们仍用V0为例:开始节点为V0,那么在应该在lowcast数组中存入所有与V0有关的边的权值,如果不存在边就用inf表示;
并且在adjvex数组中,第 i 号元素的下标对应的值表示该节点连接的另一个节点(一条边的起始节点)所以应该把adjvex中的所有元素赋值为0(表示该点与V0连接)
void Prim(AdjMatrix* G)
{
int adjvex[MAXVEX];//用来保存相关节点的下标
int lowcast[MAXVEX];//用来保存相关边的权值
lowcast[0] = 0;//初始化第一个权值为0 表示v0加入最小生成树
adjvex[0] = 0;//第一个顶点下标为0
for(int i = 1; i <= G->numV; i++)
//循环除了0以外的全部顶点
{
//将与v0有关的边的权值全部存入数组
lowcast[i] = G->Arc[0][i];
adjvex[i] = 0;
}接下来就是要去找权值最小的边,并记录这条边的结束节点K,边(V0,Vk)就是最小生成树的一条边,所以把k放进生成树中,并做上标记表示已经访问过该节点;
//找寻最小权值
for(int i = 1; i < G->numV; i++)
{
int min = INFINTIY;
int k = 0;//返回最小值的下标
int j = 1;
for(; j <= G->numV; j++)//Vj是除V0以外的顶点
{
//如果Vi和Vj有边或这条边没有被找到,且边的权值最小
if(lowcast[j] != 0 && lowcast[j] < min)
{
min = lowcast[j];//就让当前权值成为最小值
k = j;
}
}
//打印当前找到的顶点的边中 权值最小的边
printf("(%d %d)--%d ", adjvex[k], k, lowcast[k]);
//将当前顶点的权值设置为0 代表加入了生成树中
lowcast[k] = 0;回顾上文的步骤,接下来我们要找的是V0节点和Vk节点的所有邻接点,继续找权值最小的边,所以我们应该更新lowcast和adjvex数组,把与Vk有关的边(之前没被访问过的)的权值放进lowcast中,并把这个边的另一个节点Vj在adjvex中所对应的下标的值改为k;
重复上述步骤,直到所有点都加入了。
for(j = 1; j <= G->numV; j++)
{
//如果下标为k的顶点相邻的各边的权值小于此前未被加入的顶点的权值 则加入生成树中
if(lowcast[j] != 0 && G->Arc[j][k] < lowcast[j])
{
//更新lowcast和adjvex数组
lowcast[j] = G->Arc[j][k];
adjvex[j] = k;
}
}至此Prim算法写完了。
总结
最小生成树应用场景
城市铺路
网络铺设
面部识别
源码
#include
#include
#define MAXVEX 200
#define INFINTIY 65535
//prim算法
//邻接矩阵
typedef struct AdjacentMatrix
{
//顶点集
int Vertices[MAXVEX];
//边集
int Arc[MAXVEX][MAXVEX];
//顶点数 边数
int numV, numE;
}AdjMatrix;
//用带权无向邻接矩阵生成图
void creategrahp(AdjMatrix* G)
{
int n, e;//n代表顶点数 e代表边数
int vi, vj;//vi vj代表边的两个顶点对
int w;//表示边的权值
printf("要输入的顶点数和边数\n");
scanf("%d%d",&n,&e);
G->numV = n;
G->numE = e;
//图的初始化
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if(i == j)
{
//一个非带权的图 0代表没有边 1代表有边
//边不指向自己 即对角线为0
G->Arc[i][j] = 0;
}
else
{
//如果是带权的图 初始化为0或者为一个不可能的值
G->Arc[i][j] = 65535;
}
}
}
//将顶点存入数组
for(int i = 0; i < G->numV; i++)
{
printf("请输入第%d个节点的信息\n",i + 1);
scanf("%d", &G->Vertices[i]);
}
//输入边的信息
for(int i = 0; i< G->numE; i++)
{
//如果输入的是顶点的值 需要从顶点集中查找对应的下标
//如果是带权图 还要输入权的信息
printf("请输入边的信息Vi,Vj和权值w\n");
scanf("%d%d%d",&vi,&vj,&w);
G->Arc[vi][vj] = w;
//如果是带权图 等于权值
//如果是有向图 就不对称
//如果是无向图 矩阵对称
G->Arc[vj][vi] = w;
}
}
void Prim(AdjMatrix* G)
{
int adjvex[MAXVEX];//用来保存相关节点的下标
int lowcast[MAXVEX];//用来保存相关边的权值
lowcast[0] = 0;//初始化第一个权值为0 表示v0加入最小生成树
adjvex[0] = 0;//第一个顶点下标为0
for(int i = 1; i <= G->numV; i++)
//循环除了0以外的全部顶点
{
//将与v0有关的边的权值全部存入数组
lowcast[i] = G->Arc[0][i];
adjvex[i] = 0;
}
//找寻最小权值
for(int i = 1; i < G->numV; i++)//用来循环生成边的次数
{
int min = INFINTIY;
int k = 0;//返回最小值的下标
int j = 1;
for(; j <= G->numV; j++)//Vj是除V0以外的顶点
{
//如果Vi和Vj有边或这条边没有被找到,且边的权值最小
if(lowcast[j] != 0 && lowcast[j] < min)
{
min = lowcast[j];//就让当前权值成为最小值
k = j;
}
}
//打印当前找到的顶点的边中 权值最小的边
printf("(%d %d)--%d ", adjvex[k], k, lowcast[k]);
//将当前顶点的权值设置为0 代表加入了生成树中
lowcast[k] = 0;
for(j = 1; j <= G->numV; j++)//从k之后节点开始,进入下一轮迭代
{
//如果下标为k的顶点相邻的各边的权值小于此前未被加入的顶点的权值 则加入生成树中
if(lowcast[j] != 0 && G->Arc[j][k] < lowcast[j])
{
//更新lowcast和adjvex数组
lowcast[j] = G->Arc[j][k];
adjvex[j] = k;
}
}
}
}
int main()
{
AdjMatrix G;
creategrahp(&G);
Prim(&G);
system("pause");
return 0;
}