计算智能实验 BP神经网络及其应用
文章目录
- 一、需求分析
- 二、概要设计
-
- 2.1神经网络工具箱函数
- 2.2 BP神经网络模型
- 2.3 利用神经网络工具箱进行设计和方针的具体步骤
- 三、详细设计和实验代码
-
- 3.1利用神经网络进行数据分析一般步骤如下:
- 3.2使用波士顿房屋数据集进行神经网络测试:
- 四、总结:
一、需求分析
- 进行BP神经网络代码的验证学习
- 进行BP神经网络的构建
- 进行BP神经网络的训练
- 进行BP网络预测数据
二、概要设计
2.1神经网络工具箱函数
最新版的MATLAB 神经网络工具箱几乎涵盖了所有的神经网络的基本常用类型,对各种网络模型又提供了各种学习算法,我们可以根据自己的需要调用工具箱中的有关设计与训练函数,很方便地进行神经网络的设计和仿真。目前神经网络工具箱提供的神经网络模型主要用于:
(1) 数逼近和模型拟合;(2)信息处理和预测;(3)神经网络控制;(4)故障诊断。
神经网络工具箱提供了丰富的工具函数,其中有针对某一种网络的,也有通用的,
2.2 BP神经网络模型
BP 网络是一种多层前馈神经网络,由输入层、隐层和输出层组成。BP 网络模型结构见图1。网络同层节点没有任何连接,隐层节点可以由一个或多个。网络的学习过程由正向和反向传播两部分组成。在正向传播中,输入信号从输入层节点经隐层节点逐层传向输出层节点。每一层神经元的状态只影响到下一层神经元网络,如输出层不能得到期望的输出,那么转入误差反向传播过程,将误差信号沿原来的连接通路返回,通过修改各层神经元的权值,逐次地向输入层传播去进行计算,在经正向传播过程,这两个过程反复运用,使得误差信号最小或达到人们所期望的要求时,学习过程结束。

2.3 利用神经网络工具箱进行设计和方针的具体步骤
(1)确定信息表达方式:将实际问题抽象成神经网络求解所能接受的数据形式;
(2)确定网络模型:选择网络的类型,结构等;
(3)选择网络参数:如神经元,隐含层数等;
(4)确定训练模式:选择训练算法,确定训练部署,指定训练目标误差等;
(5)网络测试:选择合适的训练样本进行网络测试
三、详细设计和实验代码
3.1利用神经网络进行数据分析一般步骤如下:
(1)产生训练集和测试集。
(2)数据归一化(可选操作)
输出属性的取值不同属于同一个数量级,输入变量差异较大,因此在建立模型之前,先对数据进行归一化处理。然而,需要说明的是,归一化并非一个不可或缺的处理步骤,针对具体问题应进行具体分析,从而决定是否进行归一化;
(3)创建和训练模型
调用feedforwardnet()函数和train()函数。
(4)、仿真测试
调用sim函数。
(5)、反归一化(可选操作)
如果进行了步骤2,则需要对仿真测试结果数据按照之前归一化的规则进行反归一化操作,得到最后的真实数据.
(6)、性能分析
3.2使用波士顿房屋数据集进行神经网络测试:
使用波士顿房屋数据进行数据预测。 波士顿房屋数据集于1978年开始统计,共506个数据点,涵盖了麻省波士顿不同郊区房屋14种特征的信息。我们要使用前13个特征数据作为输入神经元,
(1)导入数据

housing中保存的数据格式如下,第1~13列为房屋属性,第14列为房屋价格

具体的,各数据特征含义可参考下图:

(2)产生训练集和测试集。
%% 随机产生训练集和测试集合
features=X;
prices=Y;
len = length(prices);
index = randperm(len);%生成1~len 的随机数,打乱样本的排序
%训练集——前70%
p_train = features(index(1:round(len*0.7)),:);%训练样本输入
t_train = prices(index(1:round(len*0.7)),:);%训练样本输出
%测试集——后30%
p_test = features(index(round(len*0.9)+1:end),:);%测试样本输入
t_test = prices(index(round(len*0.9)+1:end),:);%测试样本输出
(3)数据归一化
%%数据归一化
%输入样本归一化
[pn_train,ps1] = mapminmax(p_train');
pn_test = mapminmax('apply',p_test',ps1);
%输出样本归一化
[tn_train,ps2] = mapminmax(t_train');
(4)创建和训练模型
%% BP神经网络创建,训练和仿真测试
net = feedforwardnet(5,'trainlm');%创建网络,隐含神经元个数
net.trainParam.epochs = 5000;%设置训练次数(迭代次数)
net.trainParam.goal=0.0000001;%设置收敛误差,mse均方根误差小于这个值训练结束
net.trainParam.Ir=0.5;
net.trainParam.mc=0.6;
[net,tr]=train(net,pn_train,tn_train);%训练网络
(5)、仿真测试
%% 网络仿真
b=sim(net,pn_test);%放入到网络输出数据
(6)、反归一化(可选操作)
%% 结果分析和反归一化
%结果反归一化
predict_prices = mapminmax('reverse',b,ps2);
(7)、性能分析
%结果分析
t_test = t_test';
err_prices = abs(t_test-predict_prices);
figure;
subplot(2,1,1)
plot(err_prices);
title('误差')
legend({'误差值=房价预测值-房价实际值'})
xlabel('训练数据组数');
ylabel('误差值');
[mean(err_prices) std(err_prices)]%求平均,标准差
subplot(2,1,2)
plot(t_test);
hold on;
plot(predict_prices,'r');
xlim([1 length(t_test)]);
hold off;
title('波士顿房价')
legend({'房价实际值','房价预测值'})
xlabel('训练数据组数');
ylabel('波士顿房价值');
四、测试结果与分析
4.1通过修改feedforwardnet(前馈神经网络)函数表达式,即修改feedforwardnet(hiddenSizes,trainFcn)中hiddenSizes(隐藏神经元个数)和trainFcn(用于训练网络性能所采用的函数),来对神经网络的预测值的准确性进行比较
(1)当net = feedforwardnet(5,‘trainbr’)时,即隐藏神经元个数为5,指定训练函数为贝叶斯正则化算法。




(2)当net = feedforwardnet(12,‘trainbr’)时,即神经元个数为12,指定训练函数为贝叶斯正则化算法。
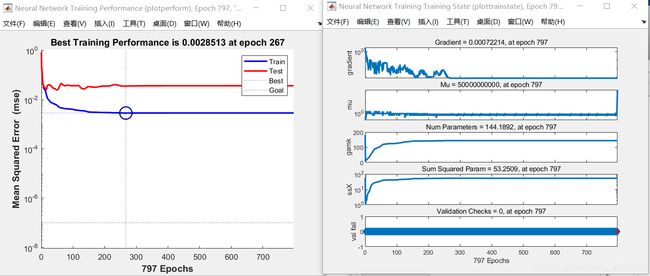


(3)当net = feedforwardnet(2,‘trainbr’)时,即神经元个数为2,指定训练函数为贝叶斯正则化算法。




四、总结:
抽取了上述测试结果中训练样本为前70%,测试样本为后30%的情况进行总结分析

通过此表我们可以看出,通过对隐藏层神经元个数和指定训练函数的不同组合,误差和标准差都基本处于2-4的范围,证明此此BP神经网络对数据预测的整体效果较好。
在输入神经元个数一定的情况下,在相同的指定训练函数即trainbr和trainlm中,随着隐藏神经元个数的增多,All Roc的值也在增大,即拟合效果较之更好。
我们也可以看出在七种指定训练函数中,traingd的迭代次数最多,处于三千多次左右,学习速度最慢,trainbr的迭代次数较多,基本处于几百次,学习速度慢,但是所有使用trainbr的All Roc的值也基本处于较高的值,而相对的trainlm的迭代次数最少,基本处于十几次左右,学习速度相对较快。
同时我们也可以看出网络层数、神经元个数的选择没有相应的理论指导,迭代次数主要受指定训练函数的影响。
通过上表我们可知,在条件一定的情况下,数据集的划分时常影响我们的准确率。但是训练集的大小和测试集大小并不是直接影响预测数据的准确性。在测试集不变的情况下,训练集大小和误差平均值没有线性关系;在训练集不变的情况下,测试集的大小和误差平均值也没有线性关系;训练集和测试集的组合大小和误差平均值大小也没有线性关系。
