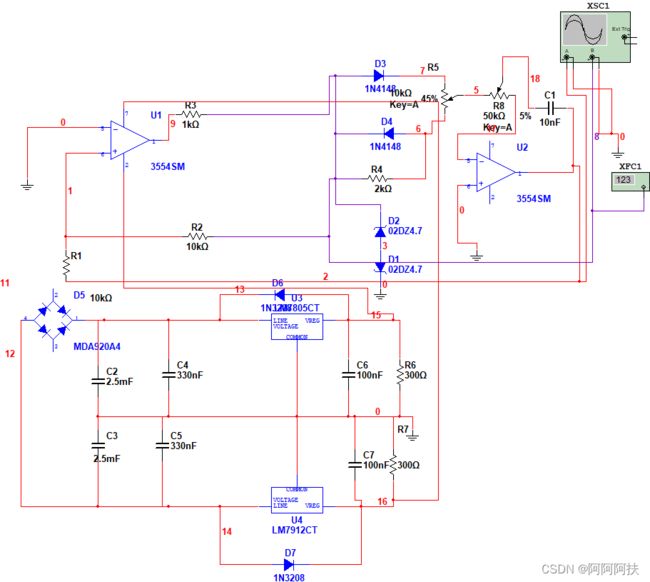
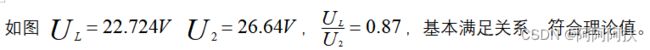电路与电子技术课程设计报告(正弦、方波-三角波、可调矩形波、可调锯齿波发生器)
目录
目录 1
1 实验任务及目的 2
1.1 实验目的 2
1.2 实验任务 2
2 直流稳压电源的设计 2
2.1 电源变压器 3
2.2 整流电路 4
2.3 滤波电路 6
2.4 稳压电路 7
2.5 对称+12V直流稳压电路 8
3 正弦信号发生器的设计 8
3.1.1 原理说明 9
3.1.2 实验电路 10
4信号发生器的设计 12
4.1 方波-三角波信号发生器 12
4.1.1 原理说明 12
4.1.2 实验电路 14
4.2 可调矩形波发生器 16
4.2.1 原理说明 16
4.2.2 实验电路 19
4.3 可调锯齿波发生器 21
4.3.1 原理说明 21
4.3.2 实验电路 22
课设总结----------------------------------------------26
1 实验任务及目的
1.1 实验目的
- 掌握三端集成稳压器组成的直流稳压电源的设计和调测。
- 掌握由运算放大器组成的信号发生器的设计方法。
- 熟悉信号发生器的一些主要性能指标
1.2 实验任务
需要完成的实验任务有:
任务 1:设计由三端集成稳压器7812和7912组成的能输出+12V和-12V的直流稳压电源电路,并完成该电路的仿真调测。
任务 2:完成由集成运放组成的信号发生器的仿真设计。所需的直流电源由任务 1 完成的电路提供。
2 直流稳压电源的设计
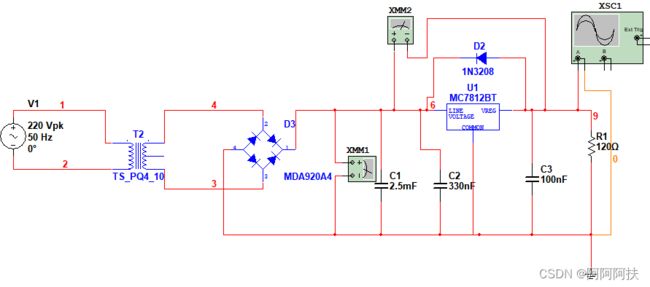
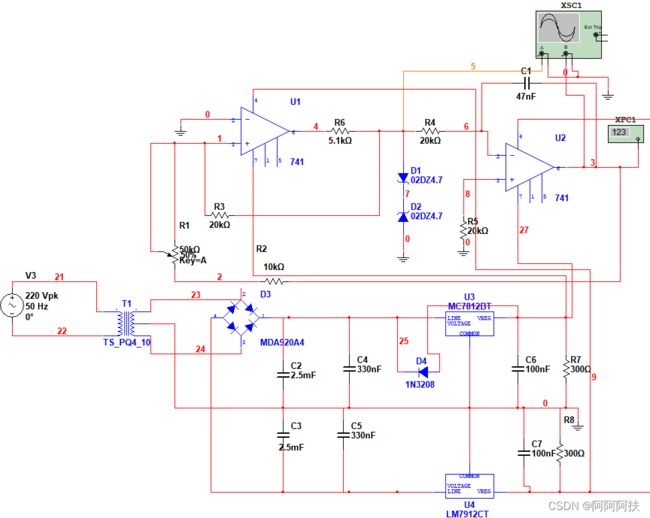
(实验总实验图)
总思路:一个大的电压,先经过变压器,将电压降低,再进行全波整流,使其相位都为正,再对整流后的电压进行滤波,,使负载电压趋于平衡,最后在进行稳压,得到一个直流电压。
主要过程如下:
2.1 电源变压器
(这里的220V指的是幅值为220V)
这里选用的变压器型号为TS_PQ4_10,降压的倍数大概为8,将220V/50HZ的交流电降到20~26V,这里不细说这个了。
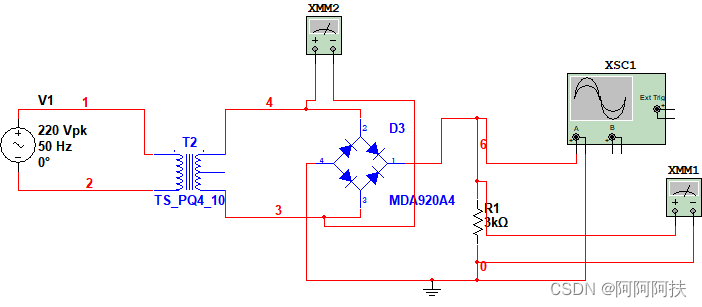
2.2 整流电路
这里采用的是单相桥式整流电路
工作原理解释:
当变压器得到的电压值为正值时,电路图中2-1脚、4-3脚的二极管导通,另外两个二极管截止,对负载上的电压进行积分运算,可以得到电压的有效值,负载上的电压为变压器输出的电压的0.9倍。
当变压器得到的电压值为负值时,电路图中3-1脚、4-2脚的二极管导通,另外两个二极管截止对负载上的电压进行积分运算,可以得到电压的有效值,负载上的电压为变压器输出的电压的0.9倍。
所以,虽然输入的电压相位有正有负,但是经过整流之后,得到的电压相位一直为正。
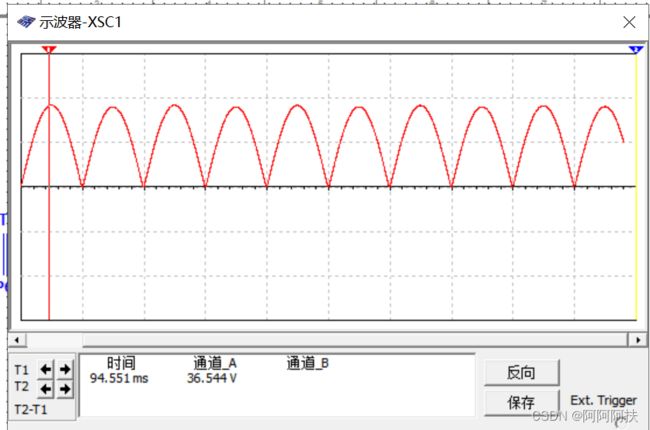
将示波器接到2脚与四脚时,观察到如下的波形。
实际上的效果如下图所示,没有理论曲线那么平滑,但总的来说,还是比较重合的。
得到这个波形结果之后,我们再看看 Ul=0.9U2 是否成立
2.3 滤波电路
下图为本电路中的整流滤波电路
滤波原理:
本电路采用的是电容滤波,电容滤波就是在整流电路的输出端并联一个比较大的电容,利用电容的充放电作用,是负载趋于平滑。(1)当变压器输出的电压处于正周期时,通过整流电路输出的电压流过负载,同时对电容进行充电。(2)当U2在波峰往下掉之后,因为电容两端的电压不会突变,它又一个放电的过程,因此电容会对RL进行放电,不会使RL两端的电压掉的太多,即电压值趋于平滑。(3)又因为电容是按指数规律放电的(衰减指数为RC,R为电容两端的等效电阻)所以,当U2降到一定幅度时,UC的下降速度低于U2的下降速度,使得UC>U2,从而导致二极管反向偏置变为截止,UC就会按指数衰减的速度下降。(4)当U2在负向时,整流电路输出的依然是相位为正的电压,则电路又会重复上述的过程。
本电路选用了2.5mF的大电容,所以这个滤波效果还是比较好的。
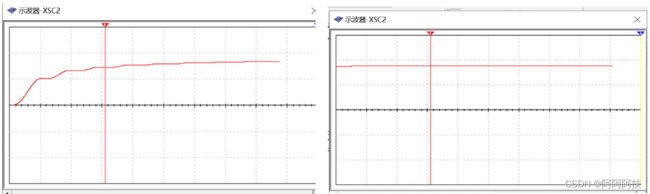
下面两幅图都是该电路负载两端的电压波形图,刚开始时,电路还有些不太稳(左图),电路主要呈现的是锯齿样的波形,后面电路稳定下来,电压趋于平衡(右图)。
同时我们也对这两端的电压进行验证。
2.4 稳压电路
本实验产生的是12V的电压,用的稳压器是7812,可以将电压稳定在12V。
实验原理:可以等效为下面这个电路
当稳压器两端的电压升高时,根据稳压管的伏安特性可知,流过稳压管的电流Iz会急剧增加,所以流过R的电流也会增大,那R得到的分压也会增大,则RL两端的电压就会相应地减少,因此,只要取参数合适的原件,R上的电压增量就可以与输入电压的增量近似相等,从而使RL两端的电压保持不变。
当稳压器两端的电压降低时,与上面正好相反,R上的电压减少量与输入电压的减少量近似相等,从而使RL两端的电压保持不变。
同时,电路中还加了整流二极管(稳压器两端),整流二极管主要应用在需要达到全波整流的低频整流电路中,连成能整流桥使用。
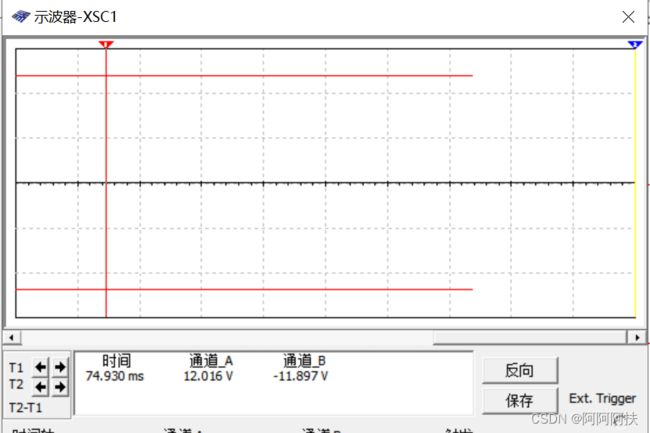
下图是RL两端的电压波形图,可以明显看出,近似一条笔直的长线(即稳压效果很好)
UL=12.013V≈12V
2.5 对称+-12V直流稳压电路
本实验是设计输出两个稳压电源的电路。需要产生12V的电压,我们采用7812的稳压管,需要产生-12V的电压,我们采用7912的稳压管。稳压原理与上文叙述的相同,只不过一个输出正电压,一个输出负电压(整流二极管相反连)。两个整流电路连同一个地,所有的元件参数都相同,电路完全对称设计。
本实验的电路图如下。
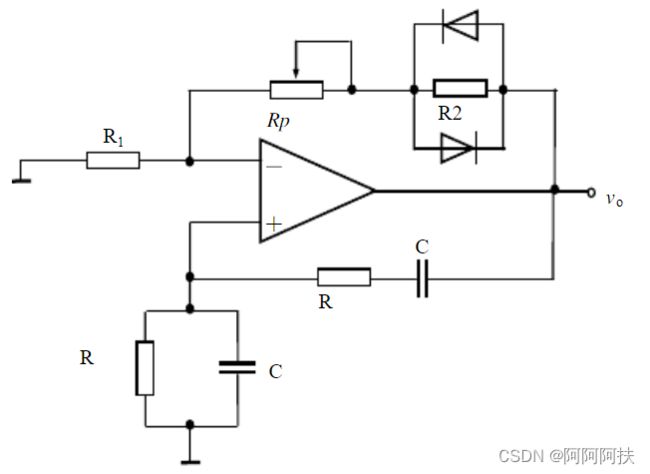
3 正弦波信号发生器的设计
实验思路:采用RC桥式正弦波发生器
电路结构的分析与设计:
电源供电方式:双电源供电、12V
电路结构:选频网络为RC选频网络,放大电路为正相比例放大电路
中心频率:文氏电桥式RC振荡器适用于低频振荡信号,一般用于产生频率为l Hz-1MHz的正弦波信号,在本实验中,中心频率选为1000Hz。
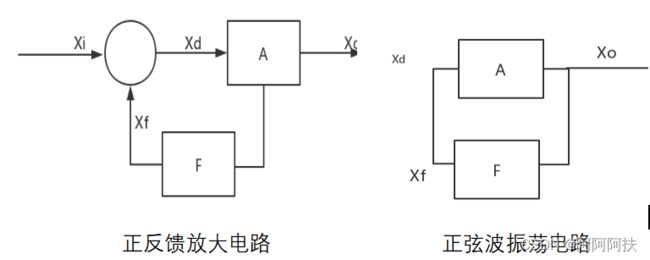
1.正弦信号发生器的震荡频率
负反馈放大器可以自激的原因是电路的相移使负反馈变成正反馈。随意这里我们将反馈直接连成正反馈电路
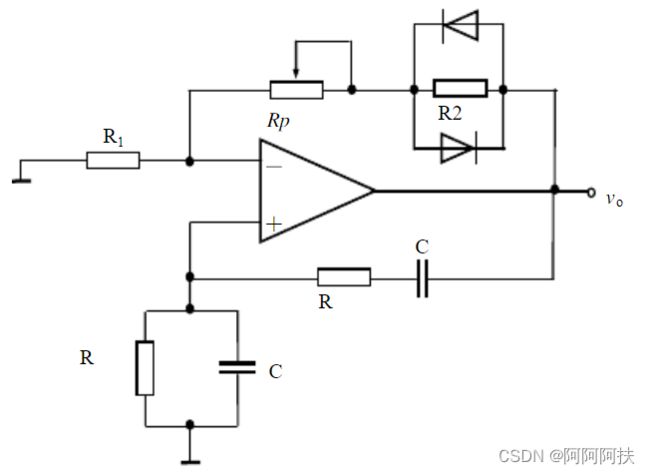
2.RC桥式正弦波信号发生器
3.1.1电路图
元件参数的计算:
(1)确定R、C值
由于fo=1/2T RC=1000Hz,得到RC-1/2TT fo=1.59*101
为了使选频网络的选频特性尽量不受集成运算放大器的输入电阻Ri和输出电阻Ro的影响,应使R满足下列关系式:Ri>>R>>Ro,一般 Ri约为几百千欧以上,Ro仅为几百欧以上。故确定R=16KQ,则C=0.01uF。
(2)确定R1、Rf
RC选频网络对于中心频率f的放大倍数为F=1/3,而回路起振条件为AF>=1。故放大电路的电压放大倍数A=(R1+Rf)/R1>=3,即 Rf/R1>=2,取 RfR1=2。而Rf-Rp+R//r d其中,rd为二极管的正向动态电阻。
为了减小输入失调电流和漂移的影响,电路应该满足直流平衡条件,即:
R=R1//Rf=16KΩ
(3)确定稳幅电路
实验证明,取R2~r 时,既能够减少二极管特性的非线性而引起的波形失真,又能起一定的稳幅作用,取R2=5.1KΩ
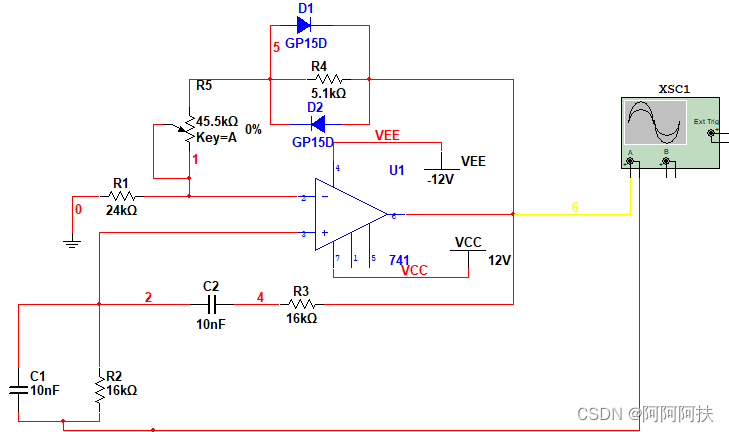
综上分析可得
实际电路
波形如下图所示,加一个频率计我们可以得到频率大概为1000HZ。
峰值为8.243V
4 信号发生器的设计
4.1 方波-三角波信号发生器
4.1.1原理说明
总的思路:由比较器和积分器组成的方波-三角波发生器,比较器主要是产生一个方形波,这个方兴波经过积分电路,变成三角波。这个过程如下图所示
实验原理:
这个电路由正相输入的滞回比较器、反向输入的滞回比较器和RC电路组成,RC即作为延迟环节,有作为反馈网络,通过RC充放电来实现电路。滞回比较器的特点是,当输入信号Ui逐渐增大或逐渐减小时,它有两个阈值,且不相等,其传输特性具有滞回性。第一个产生方波的比较器,负端接地,正端输入后面的比较器产生的三角波信号。
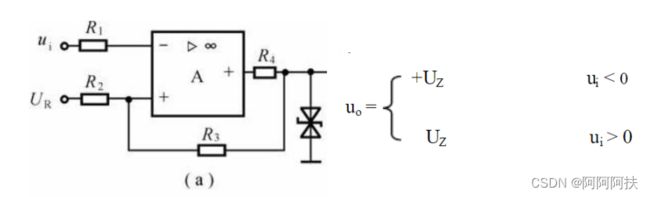
正相输入的只会比较器。
该比较器的阈值为
所以改变R3的值是可以改变阈值的,因此在电路设计中,我们将R3选用可调的电阻。当输入的信号在Uth1 和Uth2之间变化时,不会引起输出电压的跳变,就如下图所示,(1)所以当输入的得三角波电压在两者之间的时候,输出的电压为正,其电压值由后面的稳压管决定,(2)当输入的信号大于Uth1时,输出电压发成跳变,变为负值,(3)这种情况一直持续到输入的电压到了Uth2,这样就得到了发生跳变的图形。(4)在输入电压从小于Uth2到逐渐上升到UTH1之后,电压值为正变,如此循环往复得到方形波的输出结果.
这里如果调的参数比较好的话,阈值可以刚好取到最高电压和最低的电压。即输出的波形整个向左移动,刚好移到他们的突变点重合。
反向比较器用来制造三角波(图中缺少积分电路)
反相滞回比较器与正相差不多的,情况刚好是相反的。得到这个电压之后,我们在反向电路器两端加一个积分电路RC振荡电路
当输入的值为正值时,通过该电路,会变成一个负值,这个负值在通过积分电路,变成线性降低的电压。当输入一个负值电压时,通过比较器产生一个正值的电压,再通过积分电路,变成线性升高的电压。
当输入的电压保持不变时,且相位为正时,输出的电压线性降低,当相位为负的时候,输出的电压线性升高。就是以下的图形。
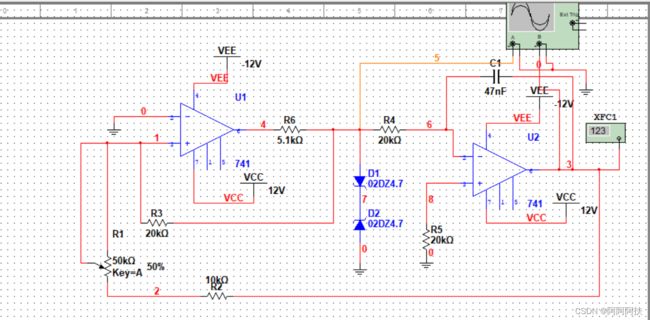
4.1.2 实验电路
电路简化如下
下面这个是将输入的电压换成我们上面稳压器产生的12V与-12V的电压(由于电路的复制不是很好,可能存在部分的电路线残缺,但大体如下)与上面的稳压电源稍有不同,这里
示波器输出的波形如下所示。
波形与理论值差不多,我们可以认为正确。
4.2 可调矩形波发生器
4.2.1 原理说明
实验总思路:本电路设计采用矩形波转变成三角波的波形转换的方法得到矩形波,在其中加一个占空比可调节电路,当积分电路正向积分时间常数远大于方向积分时间常数,或者反向积分的时间常数远大于正向积分时间常数,那么输出电压上升和下降的斜率相差会很多,这样的话就可以得到占空比可调的矩形波,同时也可以得到锯齿波。
实验原理和上面的方波-三角波的原理非常相似,方波其实是一种特殊的矩形波,方波的正负值区间刚好是一比一,而矩形波则不是一比一的比例,而且矩形波的图没有这么笔直,
如下图所示。
具体原理,在方波发生电路中,当滞回比较器的阈值点发数值较小时,可以将电容两端的电压看成为近似三角波。但是,这个三角波的线性度较差,而且带上负载后,电路的性能也会发生变化,如果RW用固定电阻,那么产生的就是三角波,而三角波作为输入又产生了方波,与我们上面的实验相同,图中采用滑动变阻器RW来调节占空比的。
因此时间常数的不同,会使输出波形的周期发生变化
利用一阶RC电路三要素法,我们可以得出
我们可以的看到,RW只改变输出波形的占空比,不改变总的周期。
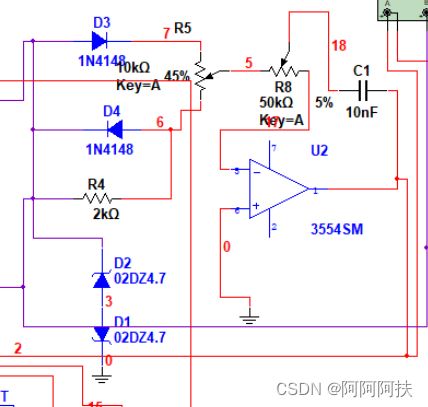
本实验调节占空比电路设计
频率可调实现(简化电路原理)
我们知道电容充放电的时间取决去Rf*C的值,因此输出波形的正负半周期时间相同。在1/2的周期内,电容充电的起始值为-UT,时间常数为Rf C,时间趋于正无穷时,电容电压趋于
本实验调节频率电路设计
4.2.2 实验电路
与上面所用的稳压电源稍有不同,因为12V的电压过大,不太适合这个这个电路的输出,所以这里把7812替换成7805,使其将电压稳定在5V。
占空比实验数据及结果
调R2=0 R1总=10KΩ
| 电阻RF |
0.15 R1总 |
0.45 R2总 |
0.95 R2总 |
| 图形 |
|||
| 电压峰值 |
8.670V |
8.561V |
8.334V |
| 占空比(正值区间比负值区间) |
大致 1.68(根据时间比出) |
大致0.77 |
大致0.02(非常小) |
这里取 R1=0.45R1总
R2总=50KΩ
调频实验结果
| R |
0.05R2总 |
0.45R2总 |
0.9R2总 |
| 波形 |
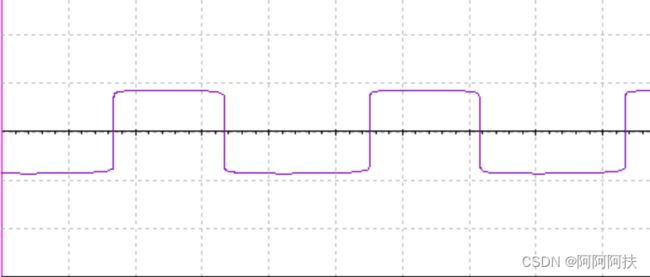 |
 |
 |
| 周期 |
1.305KHZ |
576.988HZ |
388.502HZ |
| 峰值 |
8.623V |
8.612V |
8.602V |
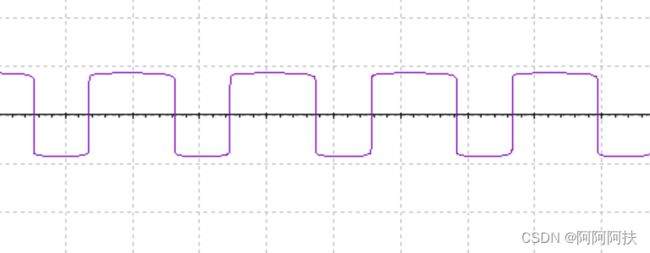
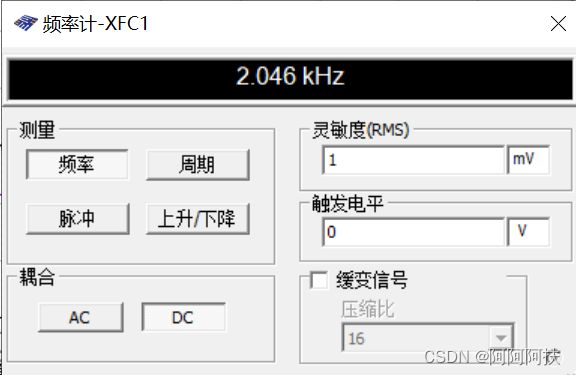
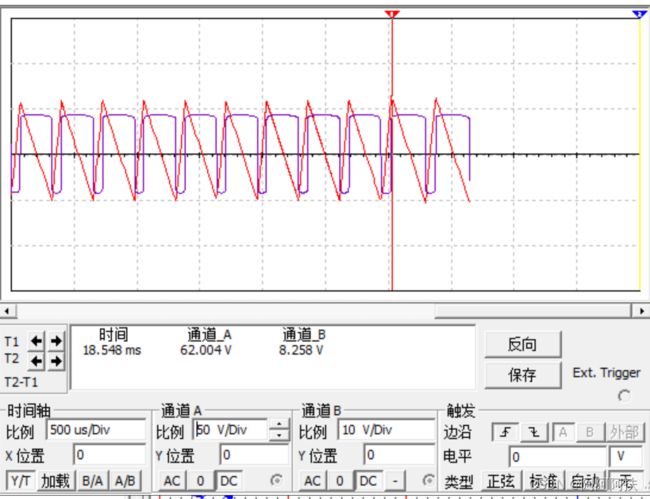
电路中峰峰值 矩形波为
矩形波峰峰值为8.643V 此时对应的频率为2.046KHZ
4.3 可调锯齿波发生器
4.3.1 原理说明
本电路设计采用矩形波转变成三角波的波形转换的方法得到矩形波,在其中加一个占空比可调节电路,当积分电路正向积分时间常数远大于方向积分时间常数,或者反向积分的时间常数远大于正向积分时间常数,那么输出电压上升和下降的斜率相差会很多,这样的话就可以得到占空比可调的矩形波,同时也可以得到锯齿波。
具体原理与上文相同,用的也是同一个电路,这里不重复说了。
4.3.2 实验电路
实验结果(保持与电容之间相连的变阻器阻值为0)
占比可调实验结果
R总=10KΩ
| 电阻RF |
0.15 R总 |
0.45 R总 |
0.95 R总 |
| 图形 |
|||
| 电压峰值 |
42.686V |
29.007V |
20.773V |
| 占空比(斜率为负的区间比斜率为正的区间) |
1.68 |
0.77 |
0.02 |
与矩形波相同的占空比。
调频实验结果
R2总=50kΩ
| R |
0.05R2总 |
0.45R2总 |
0.9R2总 |
| 波形 |
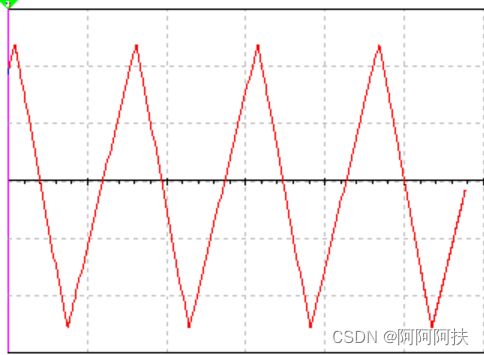 |
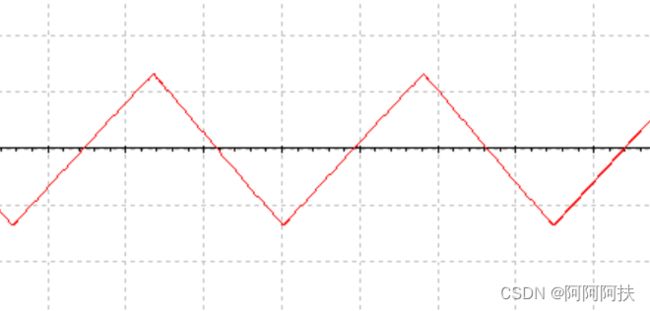 |
 |
| 频率 |
1.305KHZ |
576.988HZ |
388.502HZ |
| 峰值 |
23.072V |
12.980V |
10.716V |
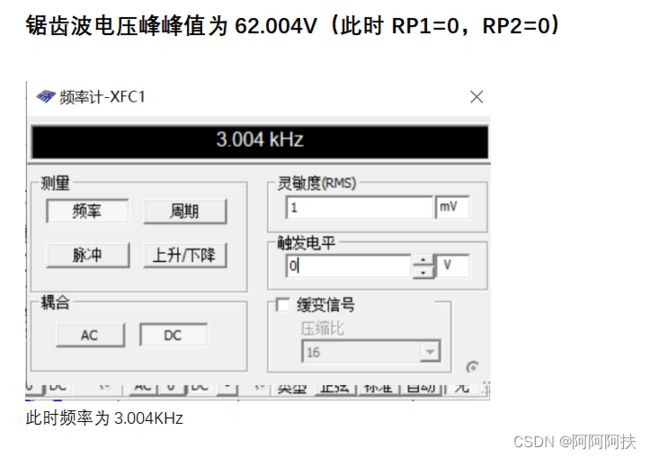
整个矩形波-锯齿波电路频率可调范围
最小348.566HZ(将RP2调到最大即50KΩ)
最大 3.103kHZ(将RP2调到最小即0)
5 课程设计总结
总的来说,这次的课程设计还是有一些难度的。直流稳压电路的设计主要是要弄清楚每个流程的输出,每部分电路的工作原理,在经过整流滤波稳压之后得到一个比较稳定的电压。在做下面的实验时,因为怕出什么差错,我都是先用Multisim里面的固定电源充当直流电,知道波形调整好之后,才用我上面得到的直流电进行调整。
正弦电路的设计也是参考了书上,只是将它的频率设定为1000hz,多了一些参数的计算。通过本次实验,我深刻理解了电压增益的含义以及电路振荡时一些关键参数。方波 三角波发生器是后面矩形波与锯齿波的基础,只有这个点了设计好了,我们才能产生占比不同的矩形波和锯齿波。其实,我们上课也讲过迟滞比较器,但是我依旧很陌生,通过这个实验,我知道了迟滞比较器的输入 阈值与输出的关系。方波和三角波是相辅相成的,他们这个电路构成一个循环,究其本质其实是傅里叶变化的应用,积分电路将方波积分得到三角波,迟滞比较器又将其还原成方波。矩形波发生器的电路原理与上文的一模一样,是不过是对其输出电压的占比,频率进行分析,得到影响他们的参数,然后在改变这些参数,得到频率与占空比都可以改变的输出矩形波与锯齿波,但是,理论上来说,这些参数的调整应该是连续的,线性可调的,但是在实验中发现,有些阻值会使电路运行到一半就突然出错,至今我也没弄到原因,有可能是测试环境的相关参数没调好。实验还发现,矩形波的峰峰值与锯齿波的峰峰值不是同时取到的。
原电路文件可以私我