作者:于雄雄 陈其友 | 旷视 MegEngine 架构师
背景
在 CV 领域中,卷积计算是扩充像素的感受野的有效方法,模型大多数的计算量都是卷积操作贡献的。因此在 CV 模型的推理性能优化中,最重要的一项工作是对卷积的优化。MegEngine 在长期的工业界实践和反馈的基础上总结得出卷积优化的基本方法有:
- 直接卷积计算优化
该方法的计算过程为逐通道进行卷积滑窗计算并累加,该优化方法对卷积的参数敏感,为了达到最优的性能,会根据各个卷积参数分别进行 kernel 优化,通用性弱,但是在 Depthwise 的卷积中却是最高效的方法。
- FFT 卷积计算优化
根据卷积的性质,利用傅立叶变换可以将卷积转换为频域上的乘法,在频域上的计算对应乘法,再使用傅立叶变换逆变换,就可以得到卷积对应的计算结果。该方法使用高性能的傅立叶变换算法,如 FFT,可以实现卷积计算的优化,算法性能完全取决于傅立叶变换的性能以及相应卷积参数。
- Im2col+matmul 卷积计算优化
由于卷积计算中有大量的乘加运算,和矩阵乘具有很多相似的特点,因此该方法使用 Im2col 的操作将卷积运算转化为矩阵运算,最后调用高性能的 Matmul 进行计算。该方法适应性强,支持各种卷积参数的优化,在通道数稍大的卷积中性能基本与 Matmul 持平,并且可以与其他优化方法形成互补。
- Winograd 卷积计算优化
Winograd 方法是按照 Winograd 算法的原理将卷积运行进行转变,达到减少卷积运算中乘法的计算总量。其主要是通过将卷积中的乘法使用加法来替换,并把一部分替换出来的加法放到 weight 的提前处理中,从而达到加速卷积计算的目的。Winograd 算法的优化局限为在一些特定的常用卷积参数才支持。
由于 direct 卷积可以直接由公式得来,而 FFT 卷积对于当前业界用到的各种参数的卷积,其性能优势远没有其他优化方法明显,对于这两者本文不做详细展开。这里主要讲述 Im2col 和 Winograd 算法的实现以及优化方法。
Im2col+Matmul 优化
Im2col 算法简介
Im2col+Matmul 方法主要包括两个步骤:
- 使用 Im2col 按照卷积核的需要将输入矩阵展开一个大的矩阵,矩阵的每一列表示卷积核需要的一个输入数据。
- 使用上面转换的矩阵进行 Matmul 运算,得到的数据就是最终卷积计算的结果。
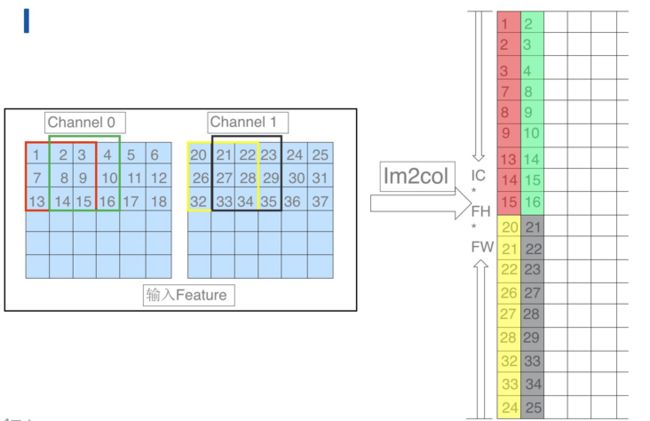
具体 Im2col 的步骤如上图所示:
- 将输入数据按照卷积窗进行展开并存储在矩阵的列中,多个输入通道的对应的窗展开之后将拼接成最终输出 Matrix 的一列。
- 以卷积的 stride 为步长展开后续的卷积窗并存在 Matrix 的下一列中。
完成 im2col 的操作之后会得到一个输入矩阵,卷积的 weights 也可以转换为一个矩阵,此时对 weights 的矩阵和 Im2col 的输出矩阵进行 Matmul 计算,就可以得到最终的卷积计算结果。
算法优化
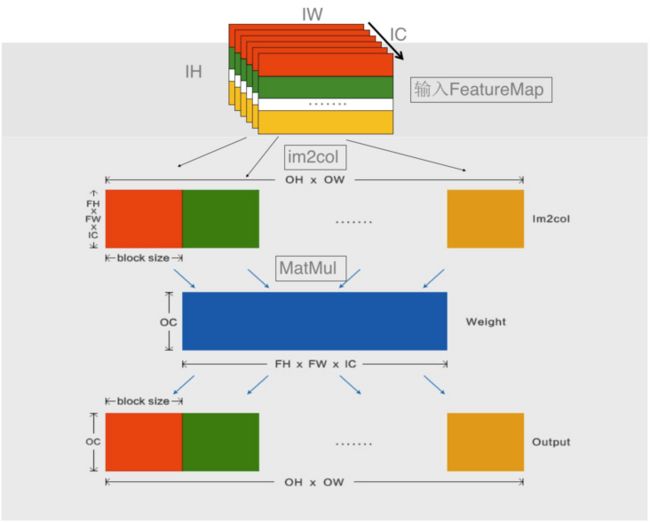
上面介绍的过程是原始 Im2col+Matmul 的过程,实际处理器在执行上面的过程中性能达不到最优,以输入 Tensor 的 shape 为 (1, IC, IH, IW),weights 的 shape 为 (OC,IC,Fh,Fw),输出 Tensor 的 shape 为 (1, OC, OH, OW) 为例,主要原因在于:
- Im2col 的输入 Tensor 需要的 CPU 内存大小为 IC*IH*IW,而按照上面 Im2col 之后所需要的内存大小为 IC*Fh*Fw*OH*OW,当卷积的 stride=1 的时候,Im2col 之后需要的内存比之前大很多。
- 由于 Im2col 之后的数据量比较大,难以全部保存在 CPU 的 Cache 中,造成后续 Matmul 计算时,读取数据会存在 Cache Miss。
- Im2col 过程中会将输入进行 relayout 操作,而在后续 Matmul 的计算中,需要对该数据进行 Pack,Pack 操作会引入非必要的读写过程。影响算法实际性能。
优化 1:对 Im2col+Matmul 过程进行分块
上面提到在 Im2col 之后,消耗的内存会超过 CPU 的 Cache 的容量,为了使这部分数据能够保存在 Cache 中,需要对 Im2col+Matmul 的整个过程进行分块,每次 Im2col+Matmul 都只对一个分块进行操作,这样就可以解决内存占用过大,超过 CPU Cache 后造成 Cache Miss 的问题。
分块优化如上图所示:Im2col 每次只对 block_size 大小的数据进行计算,得到的 Fh*Fw*IC*block_size 的数据可以保存在 Cache 中。Im2col 得到数据后,对其直接进行 Matmul 计算,将计算得到的结果写入到输出 Tensor 对应的 block_size 处就可以得到该分块处卷积的计算结果。计算完该分块之后,依次进行下一个 block_size 的计算,直到整个输入计算完成。
结合 Matmul 的相关优化知识,在进行 Matmul A*B=C 计算时将分块 Im2col 得到的数据视作 B 矩阵,A 矩阵为卷积的权重矩阵,根据 sgemm 的分块规则,以及 cache 的性质,A 矩阵会被调度并保存在 L2 上,B 矩阵基于最内层分块的一列和 A 矩阵基于最内存分块的一行以及 C 矩阵基于最内层的部分分块会被调度保存在 L1 上,因此可以通过 L1,L2 的大小以及 A 矩阵的大小,计算出所有的分块大小。下面是分块优化性能的试验结果,可以看出分块优化能有效的减少存储使用,而且还可以提升算子的计算性能。
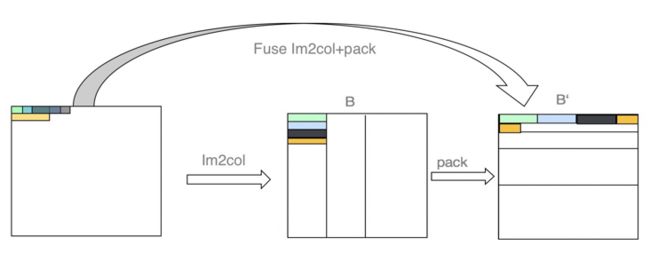
优化 2:融合 Im2col 和 Matmul PACK 数据操作部分
Im2col 过程中将多个窗的展开同时进行时,实际上是对内存的 copy 以及数据的 relayout 的过程,后续 Matmul 的 Pack 操作业是对数据的 copy 的 relayout,因此可以将上面两次数据的 copy 和 relayout 进行合并优化,减少该过程中对内存的读写次数。
如上图所示 Im2col+Matmul 的 algo 中实现了将 Im2col 和 Matmul 的 Pack 融合的优化,这样能够减少一次数据的读写操作。由于该 fuse 过程和卷积的参数直接相关,不同的卷积参数将对应不同的融合 kernel,所以不具备通用性。通用情况下我们会使用之前的 Im2col+Matmul 的做法,另外针对一些通用的卷积如:kernel=3x3,stride=2 等,因为参数固定,因此可以直接进行上述融合优化,利用这样的组合优化,既可以保证 im2col 算法的通用性,也可以确保大部分常见的卷积的性能。
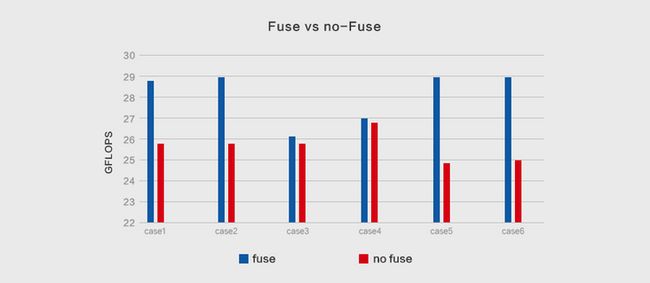
对融合之后的卷积进行性能测试,如下所示为对应的计算吞吐:
可以看出,大多数情况下,融合之后卷积会有明显的性能提升。
Winograd 优化
Winograd 算法简介
Winograd 算法能够优化卷积计算的乘法计算量,乘法计算量的优化原理可以参考相关论文。在此就不做过多介绍了。虽然 Winograd 可以优化乘法的计算量,但是会增加加法的计算量,优化这些加法的存在可以进一步提高 Winograd 算法的性能。如可以把一部分加法计算提前到 weights 的预处理中,可以把部分加法隐藏在 Winograd 预处理中的 relayout 中。类似这样的优化可以达到减少卷积计算量的目的。
如下图所示为 Winograd 卷积算法的基本步骤,主要包括:
- 把输入的 feature map 和 weight 进行 Winograd 转换;
- 把转换后 feature map 和 weight 做批量 Matmul;
- 把矩阵乘的结果进行输出转换,得到最终结果。
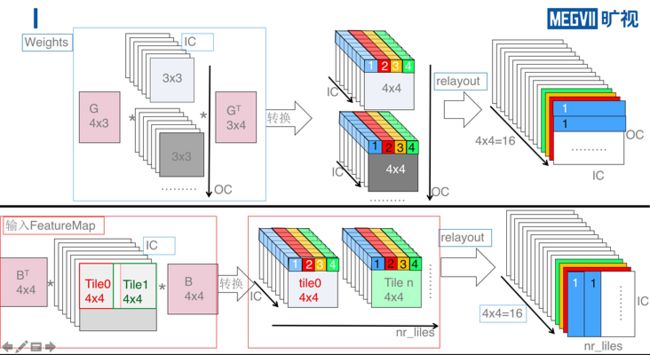
在这些主要步骤中,要如何进行 Winograd 转换,如何 relayout,以及如何进行输出转换呢?下面以 Winograd F(2x2, 3x3) 为例,详细说明下这些过程。
如上图所示,上半部分是 weights 的转换,下半部分是输入 FeatureMap 的转换。其中包括了 Winograd 转换以及 relayout 的过程。
对于 weights 的转换,首先通过 Winograd 变换矩阵 G 和 GT 分别将 3x3 的 weight 转换为 4x4 的矩阵,然后将该矩阵中相同位置的点(如图中蓝色为位置 1 的点)relayout 为一个 IC*OC 的矩阵,最终形成 4x4=16 个转换之后 weights 矩阵。
对于 FeatureMap 的转换,首先将输入 FeatureMap 按照 4x4 tile 进行切分,然后将每个 tile 通过 B 和 BT 转换为 4x4 的矩阵,矩阵 B 和 BT 为 FeatureMap 对应的 Winograd 变换矩阵,然后进行与 weight 处理相似的 relayout,转换为 16 个 nr_tiles*IC 的 FeatureMap 矩阵。
如上图所示,将上述转换后两批矩阵做矩阵乘,得到 16 个 nr_tiles*OC 的矩阵,然后将相同位置的 16 个点转换为 nr_tiles*OC 个 4x4 矩阵,再使用输出的 Winograd 变换矩阵 A 和 AT 将这些 4x4 的矩阵转换为 2x2 的输出矩阵,最后将这些矩阵写回输出矩阵中就可以得到 Winograd 卷积的最终结果。
算法优化
优化 1:weight 提前处理
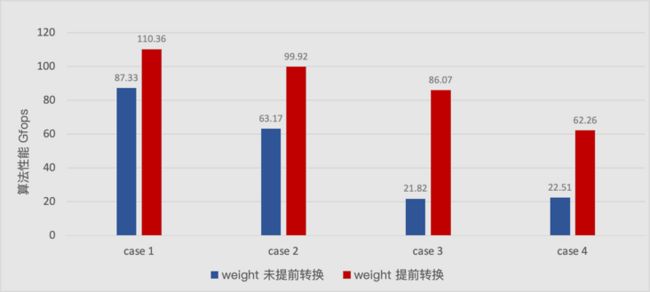
在上述 Winograd 算法的基础上,鉴于模型中的权重数据在整个 Inference 的时候已经是常量不会再改变,因此可以在真正 Inference 之前就可以对模型进行了 weights 的转换,这样可以优化在 Inference 的时候 weights 转换的开销,特别是在 IC 和 OC 较大时,weight 转换的开销非常大,所以 weights 提前转换,尤其对 Winograd 优化特别重要,下图是 Winograd 中进行 weight 提前转换和不进行 weight 提前转换时各自的性能:
从上图可以看出 weight 转换在 Winograd 中耗时占比很大,进行 weight 提前转换可以带来很大的性能收益。
优化 2:Winograd 分块优化
上述的 Winograd 算法,还会有以下缺点:
- 输入转换需要跨 channel 读写整个 feature map,数据读写对 Cache 不友好。
- feature map 转换之后,矩阵乘时需要再 PACK,数据访存增加。
针对这些问题,可以对 Winograd 算法的整个计算流程做进一步的优化,这些优化主要包括:
- 输入转换时,分块 feature map 的 tiles 进行分块,每次只进行一定数量的 tiles 计算;
- 调整分块大小适配 CPU L1 Cache,使得矩阵乘不需要 PACK;
对整个输入 feature map 进行分块后,每次只计算一个分块的 nr 个 tiles,这样就可以保证每个批量矩阵的输入数据(除了转换之后的 weight 数据)保存于 L1 Cache,不会出现 Cache miss, 而且矩阵乘时不需要 PACK。
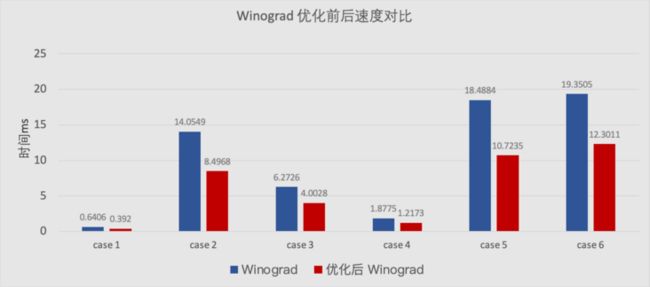
下面是分块优化前后的速度对比,可以看出分块优化对性能有显著的提升。
总结
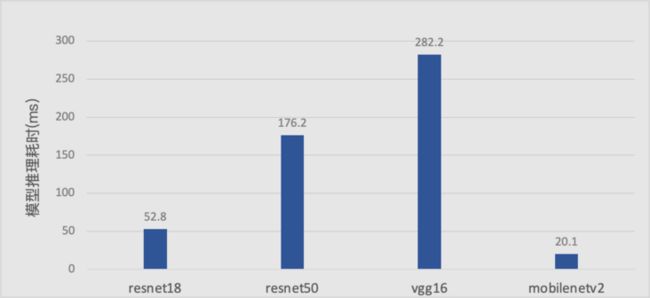
CPU 上 Inference 中有关卷积的优化有很多的途径,这里我们主要介绍了 Im2col+matmul 卷积以及 Winograd 卷积中的一些进一步优化的技术手段,通过这些方法可以进一步加速卷积计算的性能,从而加速整个模型的 Inference 性能。如下图所示是 float32 的经典网络开启相关优化后,在骁龙 855 上的测试速度:
对于具体的优化细节,大家可以结合 MegEngine 的代码实现进行研究,欢迎大家提出宝贵意见。