深度学习推荐系统之NFM(2017)结构与原理简介(代码)
系列导读
- 深度学习推荐系统之deepcrossing简单介绍与代码实现
- 深度学习推荐系统之wide & deep介绍和代码实现
- 深度学习推荐系统之deepFM介绍和代码实现
- NFM(2017)结构与原理简介(代码)
阅读前思考
NFM中的特征交叉与FM中的特征交叉有何异同,分别从原理和代码实现上进行对比分析?
介绍
NFM全称Neural Factorization Machine,是2017年由新加坡国立大学的何向南教授等人在SIGIR会议上提出的一个模型。 它擅长解决Sparse Prediction的问题。 也就是说,当模型输入特别稀疏而且特征组合对于预测结果非常重要的时候,就可以考虑是用NFM模型,像CTR预估、推荐系统都属于这类问题。 跟之前系列文章提到的Wide&Deep(Google)、DeepCross(微软)、DeepFM(华为+哈工大)模型一样都是用来处理输入数据的, 我们应该注意各个模型的适用场景、侧重点以及优缺点,灵活运用。
同样在FM的基础上引入DNN,利用非线性结构来学习更多数据信息,不同于Wide&Deep、DeepCrossing等模型,NFM的特别之处在哪?
答案: NFM使用Bi-Interaction Layer(Bi-linear interaction)(特征交叉池化层)结构来对二阶交叉信息进行处理,使交叉特征的信息能更好的被DNN结构学习,降低DNN学习更高阶交叉特征信息的难度。减轻DNN的负担,意味着不再需要更深的网络结构,从而模型参数量也减少了,模型训练更便捷。
那么NFM具体是怎么做的呢? 先看看NFM的公式:
我们对比FM,公式:
两个公式前两项一样,区别的地方第三项
NFM的思想:虽然FM很巧妙地提取了交叉特征的信息,但是,它到底局限于线性表达和二阶交互,对于特征之间的非线性交互作用很难近似表达,因而,应该用表达性更强大的神经网络结构来对交叉效应进行更灵活地表达。也就是用神经网络来替代FM中二阶隐向量内积的部分(公式第三项)。
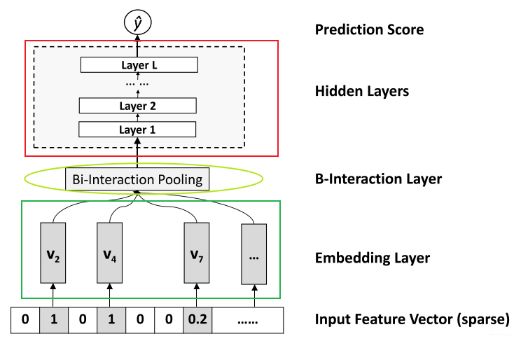
NFM 具体的网络结构图如下:
从结构图可以看出NFM共有四个部分
-
Input 和Embedding层:输入层为稀疏特征向量, 先one-hot, 然后会通过embedding处理成稠密低维。
-
Bi-Interaction Pooling layer:NFM的核心,其本质是一个pooling操作,将embedding vector集合归并为一个向量。
-
隐藏层:全连接的神经网络
-
预测层:最后一层隐藏层加上一个线性变换,作为结果输出。
下面分别对于每个部分进行详细讲解。
模型结构与原理
Input 和Embedding层
输入层为稀疏特征向量,利用FM对输入层特征进行提取,得到对应的交叉系数的隐变量,输出特征域非0的隐变量。 假设$\mathbf{v}{\mathbf{i}} \in \mathbb{R}^{k}$为第$i$个特征的embedding向量, 那么$\mathcal{V}{x}=\left{x{1} \mathbf{v}{1}, \ldots, x{n} \mathbf{v}{n}\right}$表示的下一层的输入特征。这里带上了$x_i$是因为很多$x_i$转成了One-hot之后,出现很多为0的, 这里的${x_iv_i}$是$x_i$不等于0的那些特征向量。
Bi-Interaction Pooling layer
NFM的创新之处,我们将得到的embedding层的集合输入到Bi-Interation层,它是将embedding向量的集合通过池化的操作转换为一个向量:
$\odot$表示两个向量的元素积操作,表示两个向量间对应元素相乘。因此,Bi-Interaction池化后的输出是k维的向量,也就是将特征间的二阶交叉效应映射到embedding空间中。Bi-Interaction的优势为将特征间的交叉效应以k维向量表示,同时,没有引入额外的参数,且也是在线性时间复杂度内完成的。
Bi-Interaction层不需要额外的模型学习参数,更重要的是它在一个线性的时间内完成计算,和FM一致的,即时间复杂度为$O\left(k N_{x}\right)$,$N_x$为embedding向量的数量。参考FM,可以将上式转化为:
后面代码复现NFM就是用的这个公式直接计算,比较简便且清晰。
隐藏层
这一层就是全连接的神经网络, DNN在进行特征的高层非线性交互上有着天然的学习优势,公式如下:
这里的\sigma_i是第i层的激活函数,可不要理解成sigmoid激活函数。
预测层
这个就是最后一层的结果直接过一个隐藏层,但注意由于这里是回归问题,没有加sigmoid激活:
![]()
所以, NFM模型的前向传播过程总结如下:
这就是NFM模型的全貌。
代码实现:
完整数据集:crite
源码出处:https://github.com/datawhalechina/team-learning-rs/tree/master/DeepRecommendationModel
# coding=utf-8
# Author:Jo Choi
# Date:2021-03-25
# Email:[email protected]
# Blog: caioo0.github.io
'''
数据集:criteo_sample
------------------------------
运行结果:
----------------------------
ETA: - loss: 0.3821 - binary_crossentropy: 0.3821 - auc: 0.972 - 0s 30ms/step
- loss: 0.3630 - binary_crossentropy: 0.3630 - auc: 0.9620 - val_loss: 1.3650 - val_binary_crossentropy: 1.3650 - val_auc: 0.4972
----------------------------
'''
import warnings
warnings.filterwarnings("ignore")
import itertools
import pandas as pd
import numpy as np
from tqdm import tqdm
from collections import namedtuple
import tensorflow as tf
from tensorflow.keras.layers import *
from tensorflow.keras.models import *
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler,LabelEncoder
from utils import SparseFeat, DenseFeat, VarLenSparseFeat
def data_process(data_df,dense_features,sparse_features):
"""
数据预处理,包括填充缺失值,数值处理,类别编码
:param data_df: Data_Frame格式的数据
:param dense_features: 数值特征名称列表
:param sparse_features: 离散特征名称列表
"""
#数值型特征缺失值填充0.0
data_df[dense_features] = data_df[dense_features].fillna(0.0)
for f in dense_features:
data_df[f] = data_df[f].apply(lambda x: np.log(x + 1) if x > -1 else -1)
#离散型特征缺失值填充-1
data_df[sparse_features] = data_df[sparse_features].fillna("-1")
for f in sparse_features:
#标准化
lbe = LabelEncoder()
data_df[f] = lbe.fit_transform(data_df[f])
#返回
return data_df[dense_features + sparse_features]
def build_input_layers(feature_columns):
"""
构建Input层字典,并以dense和sparse两类字典的形式返回
:param feature_columns : 数据集中的所有特征对应的特征标记
"""
# 构建input 层字典,并以dense 和 sparse 两类字典的形式返回
dense_input_dict,sparse_input_dict = {} ,{}
for fc in feature_columns:
if isinstance(fc,SparseFeat):
sparse_input_dict[fc.name] = Input(shape = (1,), name = fc.name)
elif isinstance(fc,DenseFeat):
dense_input_dict[fc.name] = Input(shape = (fc.dimension, ), name = fc.name)
return dense_input_dict, sparse_input_dict
def build_embedding_layers(feature_columns, input_layers_dict, is_linear):
# 定义一个embedding层对应的字典
embedding_layers_dict = dict()
# 将特征中的sparse特征筛选出来
sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), feature_columns)) if feature_columns else []
# 如果是用于线性部分的embedding层,其维度为1,否则维度就是自己定义的embedding维度
if is_linear:
for fc in sparse_feature_columns:
embedding_layers_dict[fc.name] = Embedding(fc.vocabulary_size , 1, name = '1d_emb_' + fc.name)
else:
for fc in sparse_feature_columns:
embedding_layers_dict[fc.name] = Embedding(fc.vocabulary_size , fc.embedding_dim , name = 'kd_emb_' + fc.name)
return embedding_layers_dict
def get_linear_logits(dense_input_dict, sparse_input_dict, sparse_feature_columns):
# 将所有的dense特征的Input层,然后经过一个全连接层得到dense特征的logits
concat_dense_inputs = Concatenate(axis=1)(list(dense_input_dict.values()))
dense_logits_output = Dense(1)(concat_dense_inputs)
# 获取linear部分sparse特征的embedding层,这里使用embedding的原因是:
# 对于linear部分直接将特征进行onehot然后通过一个全连接层,当维度特别大的时候,计算比较慢
# 使用embedding层的好处就是可以通过查表的方式获取到哪些非零的元素对应的权重,然后在将这些权重相加,效率比较高
linear_embedding_layers = build_embedding_layers(sparse_feature_columns, sparse_input_dict, is_linear=True)
# 将一维的embedding拼接,注意这里需要使用一个Flatten层,使维度对应
sparse_1d_embed = []
for fc in sparse_feature_columns:
feat_input = sparse_input_dict[fc.name]
embed = Flatten()(linear_embedding_layers[fc.name](feat_input)) # B x 1
sparse_1d_embed.append(embed)
# embedding中查询得到的权重就是对应onehot向量中一个位置的权重,所以后面不用再接一个全连接了,本身一维的embedding就相当于全连接
# 只不过是这里的输入特征只有0和1,所以直接向非零元素对应的权重相加就等同于进行了全连接操作(非零元素部分乘的是1)
sparse_logits_output = Add()(sparse_1d_embed)
# 最终将dense特征和sparse特征对应的logits相加,得到最终linear的logits
linear_logits = Add()([dense_logits_output, sparse_logits_output])
return linear_logits
class BiInteractionPooling(Layer):
def __init__(self):
super(BiInteractionPooling, self).__init__()
def call(self, inputs):
# 优化后的公式为: 0.5 * (和的平方-平方的和) =>> B x k
concated_embeds_value = inputs # B x n x k
# B x k
square_of_sum = tf.square(tf.reduce_sum(concated_embeds_value, axis = 1, keepdims = False))
# B x k
sum_of_square = tf.reduce_sum(concated_embeds_value * concated_embeds_value, axis = 1, keepdims = False)
# B x k
cross_term = 0.5 * (square_of_sum - sum_of_square)
return cross_term
def compute_output_shape(self, input_shape):
return (None, input_shape[2])
def get_bi_interaction_pooling_output(sparse_input_dict, sparse_feature_columns, dnn_embedding_layers):
# 只考虑sparse的二阶交叉,将所有的embedding拼接到一起
# 这里在实际运行的时候,其实只会将那些非零元素对应的embedding拼接到一起
# 并且将非零元素对应的embedding拼接到一起本质上相当于已经乘了x, 因为x中的值是1(公式中的x)
sparse_kd_embed = []
for fc in sparse_feature_columns:
feat_input = sparse_input_dict[fc.name]
# B x 1 x k
_embed = dnn_embedding_layers[fc.name](feat_input)
sparse_kd_embed.append(_embed)
# 将所有sparse的embedding拼接起来,得到 (n, k)的矩阵,其中n为特征数,k为embedding大小
# B x n x k
concat_sparse_kd_embed = Concatenate(axis = 1)(sparse_kd_embed)
pooling_out = BiInteractionPooling()(concat_sparse_kd_embed)
return pooling_out
def get_dnn_logits(pooling_out):
# dnn层,这里的Dropout参数,Dense中的参数都可以自己设定, 论文中还说使用了BN, 但是个人觉得BN和dropout同时使用
# 可能会出现一些问题,感兴趣的可以尝试一些,这里就先不加上了
dnn_out = Dropout(0.5)(Dense(1024, activation='relu')(pooling_out))
dnn_out = Dropout(0.5)(Dense(512, activation='relu')(dnn_out))
dnn_out = Dropout(0.3)(Dense(256, activation='relu')(dnn_out))
dnn_logits = Dense(1)(dnn_out)
return dnn_logits
def NFM(linear_feature_columns, dnn_feature_columns):
# 构建输入层,即所有特征对应的Input()层,这里使用字典的形式返回,方便后续构建模型
dense_input_dict, sparse_input_dict = build_input_layers(linear_feature_columns + dnn_feature_columns)
# 将linear部分的特征中sparse特征筛选出来,后面用来做1维的embedding
linear_sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), linear_feature_columns))
# 构建模型的输入层,模型的输入层不能是字典的形式,应该将字典的形式转换成列表的形式
# 注意:这里实际的输入与Input()层的对应,是通过模型输入时候的字典数据的key与对应name的Input层
input_layers = list(dense_input_dict.values()) + list(sparse_input_dict.values())
# linear_logits由两部分组成,分别是dense特征的logits和sparse特征的logits
linear_logits = get_linear_logits(dense_input_dict, sparse_input_dict, linear_sparse_feature_columns)
# 构建维度为k的embedding层,这里使用字典的形式返回,方便后面搭建模型
# embedding层用户构建FM交叉部分和DNN的输入部分
embedding_layers = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False)
# 将输入到dnn中的sparse特征筛选出来
dnn_sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), dnn_feature_columns))
pooling_output = get_bi_interaction_pooling_output(sparse_input_dict, dnn_sparse_feature_columns, embedding_layers) # B x (n(n-1)/2)
# 论文中说到在池化之后加上了BN操作
pooling_output = BatchNormalization()(pooling_output)
dnn_logits = get_dnn_logits(pooling_output)
# 将linear,dnn的logits相加作为最终的logits
output_logits = Add()([linear_logits, dnn_logits])
# 这里的激活函数使用sigmoid
output_layers = Activation("sigmoid")(output_logits)
model = Model(input_layers, output_layers)
return model
if __name__ == "__main__":
# 读取数据
data = pd.read_csv('./data/criteo_sample.txt')
# 划分dense和sparse特征
columns = data.columns.values
dense_features = [feat for feat in columns if 'I' in feat]
sparse_features = [feat for feat in columns if 'C' in feat]
# 简单的数据预处理
train_data = data_process(data, dense_features, sparse_features)
train_data['label'] = data['label']
# 将特征分组,分成linear部分和dnn部分(根据实际场景进行选择),并将分组之后的特征做标记(使用DenseFeat, SparseFeat)
linear_feature_columns = [SparseFeat(feat, vocabulary_size=data[feat].nunique(),embedding_dim=4)
for i,feat in enumerate(sparse_features)] + [DenseFeat(feat, 1,)
for feat in dense_features]
dnn_feature_columns = [SparseFeat(feat, vocabulary_size=data[feat].nunique(),embedding_dim=4)
for i,feat in enumerate(sparse_features)] + [DenseFeat(feat, 1,)
for feat in dense_features]
# 构建NFM模型
history = NFM(linear_feature_columns, dnn_feature_columns)
history.summary()
history.compile(optimizer="adam",
loss="binary_crossentropy",
metrics=["binary_crossentropy", tf.keras.metrics.AUC(name='auc')])
# 将输入数据转化成字典的形式输入
train_model_input = {name: data[name] for name in dense_features + sparse_features}
# 模型训练
history.fit(train_model_input, train_data['label'].values,
batch_size=64, epochs=6, validation_split=0.2, )Model: "functional_1"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
C1 (InputLayer) [(None, 1)] 0
__________________________________________________________________________________________________
******
__________________________________________________________________________________________________
Epoch 1/6
3/3 [==============================] - ETA: 0s - loss: 2.7443 - binary_crossentropy: 2.7443 - auc: 0.345 - 1s 321ms/step - loss: 2.2624 - binary_crossentropy: 2.2624 - auc: 0.3496 - val_loss: 1.9658 - val_binary_crossentropy: 1.9658 - val_auc: 0.4915
Epoch 2/6
3/3 [==============================] - ETA: 0s - loss: 1.7556 - binary_crossentropy: 1.7556 - auc: 0.530 - 0s 30ms/step - loss: 1.6137 - binary_crossentropy: 1.6137 - auc: 0.3837 - val_loss: 1.6605 - val_binary_crossentropy: 1.6605 - val_auc: 0.4929
Epoch 3/6
3/3 [==============================] - ETA: 0s - loss: 0.9150 - binary_crossentropy: 0.9150 - auc: 0.453 - 0s 28ms/step - loss: 0.7229 - binary_crossentropy: 0.7229 - auc: 0.5839 - val_loss: 1.2336 - val_binary_crossentropy: 1.2336 - val_auc: 0.4915
Epoch 4/6
3/3 [==============================] - ETA: 0s - loss: 0.7438 - binary_crossentropy: 0.7438 - auc: 0.770 - 0s 27ms/step - loss: 0.6271 - binary_crossentropy: 0.6271 - auc: 0.7781 - val_loss: 1.0983 - val_binary_crossentropy: 1.0983 - val_auc: 0.4929
Epoch 5/6
3/3 [==============================] - ETA: 0s - loss: 0.4732 - binary_crossentropy: 0.4732 - auc: 0.916 - 0s 28ms/step - loss: 0.5352 - binary_crossentropy: 0.5352 - auc: 0.9232 - val_loss: 1.1800 - val_binary_crossentropy: 1.1800 - val_auc: 0.4957
Epoch 6/6
3/3 [==============================] - ETA: 0s - loss: 0.3821 - binary_crossentropy: 0.3821 - auc: 0.972 - 0s 30ms/step - loss: 0.3630 - binary_crossentropy: 0.3630 - auc: 0.9620 - val_loss: 1.3650 - val_binary_crossentropy: 1.3650 - val_auc: 0.4972
参考:
-
王喆 《深度学习推荐系统》
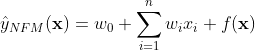
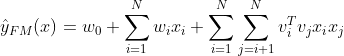

![f_{B I}\left(\mathcal{V}_{x}\right)=\frac{1}{2}\left[\left(\sum_{i=1}^{n} x_{i} \mathbf{v}_{i}\right)^{2}-\sum_{i=1}^{n}\left(x_{i} \mathbf{v}_{i}\right)^{2}\right]](http://img.e-com-net.com/image/info8/4f62398352464433a618cb5f7d06dc7c.gif)