逻辑回归算法c语言_基于GBDT算法+LR逻辑回归处理信用卡交易反欺诈

本项目需要解决的问题

通过利用信用卡历史交易信息，进行机器学习，构建信用卡反欺诈预测模型，提前发现客户信用卡被盗刷时间

建模思路

场景分析

背景：

数据集包含由欧洲持卡人于2013年9月使用信用卡进行交的数据，此数据集显示两天内发生的交易。

算法选择：

1. 根据历史记录数据学习并对信用卡持卡人是否会发生被盗刷进行预测，二分类监督学习场景，选择逻辑斯蒂回归（Logistic Regression）算法。

2. 数据为结构化数据，不需要做特征抽象，但需要做特征缩放。

数据预处理

• 导入数据

credit = pd.read_csv('creditcard.csv')
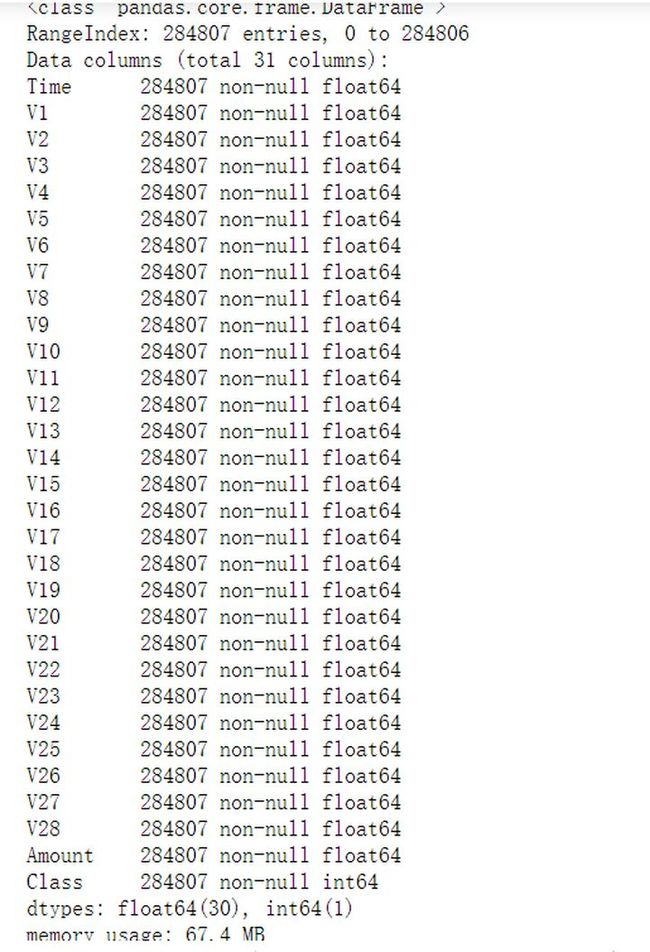
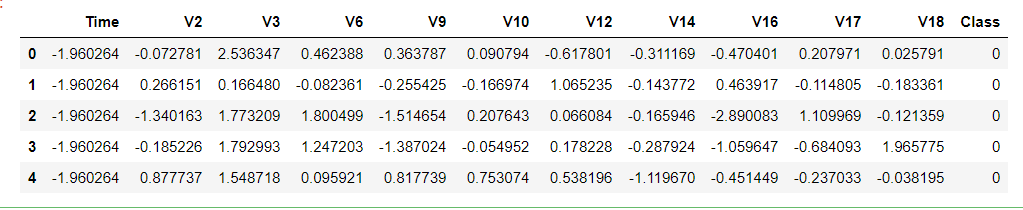
credit.head()

• 查看数据基本信息

credit.info()

一共有28万行31列数据，没有缺失值，方便后续处理

特征工程

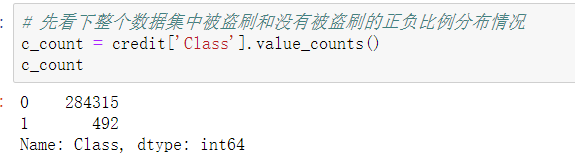
• 查看正负样本的分布情况

将正负样本分布情况可视化

通过上面的图和数据可知，存在492例盗刷，占总样本的0.17%，由此可知，这是一个明显的数据类别不平衡问题，稍后我们采用过采样(增加数据)的方法对这种问题进行处理。

• 特征缩放

Amount变量和Time变量的取值范围与其他变量相差较大，所以要对其进行特征缩放sklearn.preprocessing.StandarScaler
作用：去均值和方差归一化，只针对某一个维度。

使得新的X数据集方差为1，均值为0

from sklearn.preprocessing import StandardScaler
scaler =  StandardScaler()
credit['Time']  =scaler.fit_transform(credit[['Time']])
credit['Amount'] = scaler.fit_transform(credit[['Amount']])

• 特征选择

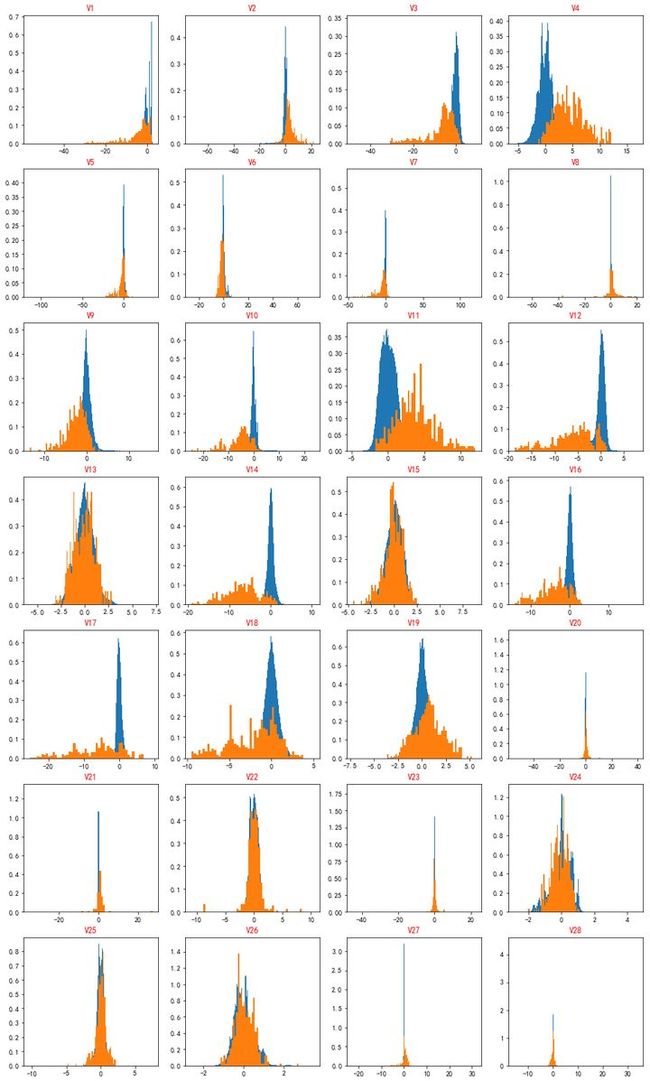
V1-V29经过脱敏处理，我们不能知道每个特征的具体含义。但是有的变量在信用卡被盗刷和正常两种情况下没有明显的区别，这样的特征不利于逻辑回归模型训练，还会增加模型复杂度和训练时间，因此这一步要找出这些变量，然后剔除。 通过频率分布直方图，可以直观地看出不同指标在两种场景中的分布，如果一致，则该特征删除。

# 以循环的方式，分别取出每个指标在两种场景的分布数据，绘制频率分布直方图
#建立画板
plt.figure(figsize=(4*4,9*4))  

for i,col in enumerate(cols):
    #每一轮循环新建一个画布，绘制该特征的直方图
    ax=plt.subplot(9,4,i+1)
    #该特征在正常情况下的数据
    credit_class0_v = credit_class0[col]
    #该特征在被盗刷情况下的数据
    credit_class1_v = credit_class1[col]

    # 由于数据集非常不平衡，易于出现某个图被另一个完全遮挡，所以使用频率分布，同时通过设置直方图的矩形数目，将两种场景的数据图区分开来，便于观察
    plt.hist(credit_class0_v,density=True,bins=500)
    plt.hist(credit_class1_v,density=True,bins=50)
    plt.title(col,color='red',fontsize=12)
plt.show()

上图是不同变量在信用卡被盗刷和信用卡正常的不同分布情况，我们将选择在不同信用卡状态下的分布有明显区别的变量。因此剔除变量V8、V13 、V15 、V20、V21 、V22、 V23 、V24 、V25 、V26 、V27 和V28变量。

credit.drop(['V8', 'V13', 'V15', 'V20', 'V21', 'V22','V23', 'V24', 'V25', 'V26', 'V27', 'V28'],axis = 1,inplace=True)

• 对特征的重要性进行排序，以进一步减少变量

利用GBDT梯度提升决策树进行特征重要性排序

from sklearn.ensemble import GradientBoostingClassifier

data =  credit.iloc[:,0:-1]
target = credit[['Class']]
# 构建模型
gbdt = GradientBoostingClassifier()
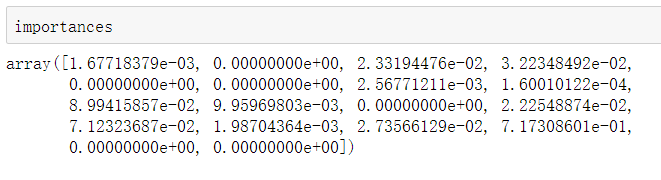
importances = gbdt.feature_importances_
# 返回各个特征的重要性，数值越大，特征越重要

将这个特征重要性以图表形式可视化显示
# 转换成pandas的DataFrame
importances_df = pd.DataFrame(importances,index = data.columns,columns=['importance'])

# 按特征重要性降序排列
importances_df= importances_df.sort_values(by='importance',ascending=False)

# 画柱状图
plt.figure(figsize=(12,9))
ax = plt.subplot(1,1,1)
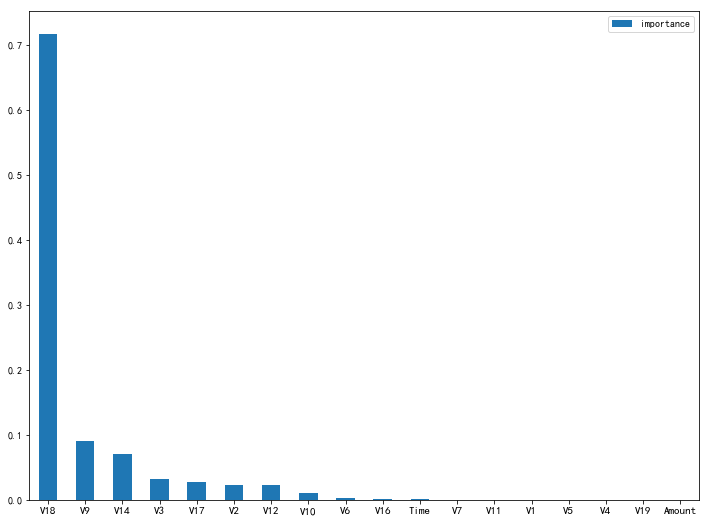
importances_df.plot(kind='bar',ax=ax)
plt.xticks(np.arange(0,18),importances_df.index,rotation=0,fontsize=11)

plt.show()

图中V7之后的特征几乎看不到柱状图，故剔除

# 根据特征重要性结果，去掉V1 V4 V5 V7 V11 V19 Amount
credit.drop(['V7','V11','V1','V5','V4','V19','Amount'],inplace=True,axis=1)
credit.head()

• 本案例还有一个样本严重不平衡问题待解决

目标变量“Class”正常和被盗刷两种类别的数量差别较大，会对模型学习造成困扰。举例来说，假如有100个样本，其中只有1个是被盗刷样本，其余99个全为正常样本，那么学习器只要制定一个简单的方法：即判别所有样本均为正常样本，就能轻松达到99%的准确率。而这个分类器的决策对我们的风险控制毫无意义。因此，在将数据代入模型训练之前，我们必须先解决样本不平衡的问题。

**现对该业务场景进行总结如下：**

1. 过采样（oversampling），增加正样本使得正、负样本数目接近，然后再进行学习。

2. 欠采样（undersampling），去除一些负样本使得正、负样本数目接近，然后再进行学习。

本次处理样本不平衡采用的方法是**过采样**，具体操作使用SMOTE（Synthetic Minority Oversampling Technique），SMOET的基本原理是：采样最邻近算法，计算出每个少数类样本的K个近邻，从K个近邻中随机挑选N个样本进行随机线性插值，构造新的少数样本，同时将新样本与原数据合成，产生新的训练集。

# SMOTE过采样

from imblearn.over_sampling import SMOTE
smote = SMOTE()
# 使用SMOTE 的fit_resample 方法进行过采样，返回新样本与原数据合成的数据集
data = credit.drop(['Class'],axis=1)
target =  credit['Class']

# 拆分训练集，测试集
from sklearn.model_selection import train_test_split
train_X,test_X,train_y,test_y = train_test_split(data,target,train_size=0.8)

# 只对训练集进行SMOTE过采样，测试集样本数据不平衡没关系
data_resample,target_resample = smote.fit_resample(train_X,train_y)

训练前只有19万条数据，训练后增加至39万条数据

模型训练

• 使用默认参数建立逻辑斯蒂回归

# 使用逻辑斯蒂回归计算
from sklearn.linear_model import LogisticRegression
logistic= LogisticRegression()

# 训练
logistic.fit(data_resample,target_resample)

# 查看模型准确度
logistic.score(data_resample,target_resample)
0.9319372878673302
logistic.score(test_X,test_y)
0.9307809999472416

# 这个案例重要的是召回率
from sklearn.metrics import confusion_matrix
y_ = logistic.predict(test_X)
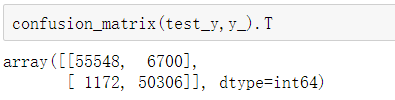
confusion_matrix(test_y,y_).T

recall =  50306/(50306+6700)
recall
0.882468512086447

LR模型在训练集和测试集上的准确度均为0.93，非常稳定；
LR模型的召回率仅有0.88，非常地。就是说100个信用卡盗刷时间，还有12件不能预测。

• 利用GridSearchCV进行交叉验证和模型参数自动调优

# 使用GridSearchCV网格搜索和交叉验证寻找更好的参数
from sklearn.model_selection import GridSearchCV

logistic=LogisticRegression()
#C :正则惩罚项系数
param_grid ={
                'C':[0.1,1,10],
                'tol':[1e-5,1e-4,1e-3]
}

gv =  GridSearchCV(logistic , param_grid,n_jobs=-1,cv=5)
gv.fit(data_resample,target_resample)

#最优参数
gv.best_params_
{'C': 1, 'tol': 1e-05}

#优化后的模型准确率
gv.best_score_
0.9335974602121512    # 0.93和使用默认参数的准确率一直，再次表明逻辑回归模型非常稳定

# 优化后的模型召回率
y_ = gv.predict(test_X)
cm = confusion_matrix (test_y,y_).T
recall =  50306/(6700+50306)
0.882468512086447    # 召回率也没有明显提升

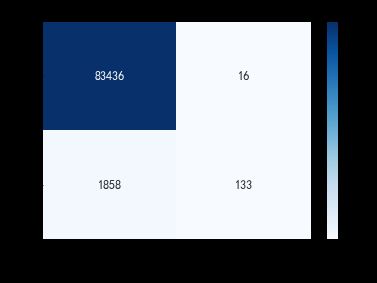
#绘制混淆矩阵可视化
cm_df =  pd.DataFrame(cm)
sns.heatmap(cm_df,annot=True,fmt='.20g',annot_kws={'size':12},cmap='Blues')
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

plt.xlabel('真实值0/1',fontsize=14)
plt.ylabel('预测值0/1',fontsize=14)

plt.title('Recall %.3f%% ' %recall )
plt.show()

优化后，召回率并没有明显的提升

模型评估

解决不同的问题，通常需要不同的指标来度量模型的性能。例如我们希望用算法来预测癌症是否是恶性的，假设100个病人中有5个病人的癌症是恶性，对于医生来说，尽可能提高模型的**查全率（recall）比提高查准率（precision）**更为重要，因为站在病人的角度，**发生漏发现癌症为恶性比发生误判为癌症是恶性更为严重。**

由此可见就上面的两个算法而言，明显lgb过拟合了，考虑到样本不均衡问题，故应该选用简单一点的算法（逻辑回归）来减少陷入过拟合的陷阱。

## 考虑设置阈值，来调整预测被盗刷的概率，依次来调整模型的召回率（Recall）

thresholds = [0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
# 例如第一个阈值，只要大于0.05，就算作盗刷，这样查全率就很高，但是同时也伤了很多人，很多不是盗刷的都被系统检测为盗刷，这样卡被冻结，给用户造成麻烦，影响用户留存率

logistic= LogisticRegression()
logistic.fit(train_X,train_y)
y_proba = logistic.predict_proba(test_X)
from sklearn.metrics import roc_auc_score,confusion_matrix
aucs=[]
recalls=[]
precisions=[]
accuracys=[]
F1s=[]
for threshold in thresholds:
    pred_y = y_proba[:,1]>=threshold
    # 计算auc面积
    auc_ = roc_auc_score(test_y,pred_y)
    aucs.append(auc_)
    
    # 计算召回率
    cm = confusion_matrix(test_y,pred_y).T
    recall_ = cm[1,1] / (cm[0,1]+cm[1,1])
    recalls.append(recall_)
    
    # 计算精确率：预测为真的样本中有多少预测正确
    precision_ = cm[1,1] /(cm[1,0]+cm[1,1]) 
    precisions.append(precision_)
    
    # 准确率：所有样本，有多少预测正确
    accuracy_ = (cm[0,0] + cm[1,1])/cm.sum()
    accuracys.append(accuracy_)
    
    # F—measure：准确率和召回率有时候会出现矛盾，此时需要综合考虑两个指标，最常见的方法就是F-measure。F-Measure是Precision和Recall加权调和平均：
    # F = (α+1）*P*R / α2(P+R),如果α=1，就是最常见的F1 F1= 2*P*R / (P+R),可知F1综合了P和R的结果，当F1较高时则能说明试验方法比较有效。
    # 如果是做搜索，那就是保证召回的情况下提升准确率；如果做疾病监测、反垃圾，则是保准确率的条件下，提升召回。
    F1_ = 2*precision_ * recall_ /(precision_ + recall_)
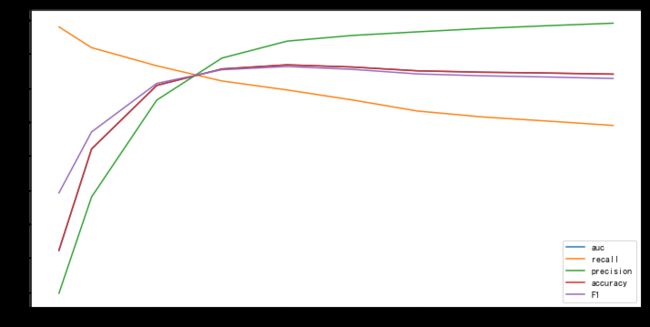
    F1s.append(F1_)

# 趋势图

# 以曲线形式展现更加直观
plt.plot(thresholds,aucs,label='auc')
plt.plot(thresholds,recalls,label='recall')
plt.plot(thresholds,precisions,label='precision')
plt.plot(thresholds,accuracys,label='accuracy')
plt.plot(thresholds,F1s,label='F1')

plt.legend()
plt.show()

由上图所见，随着阈值逐渐变大，Recall rate逐渐变小，Precision rate逐渐变大，AUC值先增后减

# 找出模型最优的阈值

precision和recall是一组矛盾的变量。从上面混淆矩阵和PRC曲线可以看到，阈值越小，recall值越大，模型能找出信用卡被盗刷的数量也就更多，但换来的代价是误判的数量也较大。随着阈值的提高，recall值逐渐降低，precision值也逐渐提高，误判的数量也随之减少。**通过调整模型阈值，控制模型反信用卡欺诈的力度，若想找出更多的信用卡被盗刷就设置较小的阈值，反之，则设置较大的阈值。**

当模型阈值设置较小的值，确实能找出更多的信用卡被盗刷的持卡人，但随着误判数量增加，不仅加大了贷后团队的工作量，也会降低正常情况误判为信用卡被盗刷客户的消费体验，从而导致客户满意度下降。

经过调研，阈值设置为0.68时，边际利润和边际成本达到平衡。