中文信息处理(三)—— 词性标注
目录
- 1. 什么是词性标注?
- 2. 词性标注的难点
-
- 2.1 兼类现象
-
- 2.1.1 英语词的兼类现象
- 2.1.2 汉语词的兼类现象
- 3. 词性标记集
- 4. 基于HMM的词性标注
-
- 4.1 什么是基于HMM的词性标注?
-
- 4.1.1 HMM的提出
- 4.1.2 数学角度
- 4.1.3 Maekov模型
- 4.2 HMM的形式化描述
-
- 4.2.1 几个概率
- 4.2.2 三大问题的解决方案
- 4.3 参数估计
- 4.4 维特比(viterbi)算法求最大概率
-
- 4.4.1 Viterbi算法思想
- 4.4.2 Viterbi变量的引入
- 4.2.3 算法复杂度
- 4.2.4 局限性
- 5. 基于转换的词性标注
-
- 5.1 基本思想
- 5.2 转换规则(改写规则+激活环境)
- 5.3 算法实现
- 5.4 算法描述
- 5.5 基于转换方法评价
- 6. 基于分类思想的词性标注
1. 什么是词性标注?
词性标注:又称词类标注,是为词序列中的词赋予词性标记,属于序列标注问题。是简单、非常有用的语言学分析 。
2. 词性标注的难点
2.1 兼类现象
2.1.1 英语词的兼类现象
DeRose(1988)对Brown语料库进行统计:
无歧义的词: 35,340 歧义词: 4,100(11.6%),其中
2个标记:3,764
3个标记:264
4个标记:61
5个标记:12
6个标记:2
7个标记:1
2.1.2 汉语词的兼类现象
| 兼类数 | 兼类词数 | 百分比 | 到词及词性标记 |
|---|---|---|---|
| 5 | 3 | 0.01% | 和c-n-p-q-v |
| 4 | 20 | 0.04% | 光a-d-n-v |
| 3 | 126 | 0.23% | 画n-q-v |
| 2 | 1475 | 2.67% | 锁n-v |
| 合计 | 1624 | 2.94% | 总词数:55191 |
虽然兼类词的比例较小,但很多是常用词。大部分兼类词所兼词类出现频繁 ,因而对兼类词的处理很重要。
3. 词性标记集
北大的词性标记集,共39种:
• Ag: 形语素, 形容词性语素
• a 形容词
• ad 副形词,直接作状语的形容词
• an 名形词,具有名词功能的形容词,如:这些/r 国家/n 和/c 地区/n 的/u 努力/an
• b 区别词
• c 连词
• Dg 副词性语素
• d 副词
• e 叹词
• f方位词
• g 语素
• h 前接成分
• i 成语
• j 简称略语
• k 后接成分
• l 习用语 尚未成为成语
• m 数词
• Ng 名语素 名词性语素
• n 名词
• nr 人名
• ns 地名
• nt 机构团体
• nz 其他专名
• o 拟声词
• p 介词
• q 量词
• r 代词
• s 处所词
• Tg 时语素 时间词性语素
• t 时间词 。
• u 助词
• Vg 动语素 动词性语素
• v 动词
• vd 副动词 直接作状语的动词
• vn 名动词 具有名词功能的动词
• w 标点符号
• x 非语素字
• y 语气词
• z 状态词
早期的词性标注:
- 用规则归纳语言现象,解决兼类问题。
- 简单的概率法标注:不考虑上下文,为兼类词赋予可能性最大的词性标记。(局限:没有考虑上下文 )
4. 基于HMM的词性标注
4.1 什么是基于HMM的词性标注?
4.1.1 HMM的提出
不是俄罗斯数学家Markov提出,但与Markov链有关。
美国数学家鲍姆(Leonard E. Baum)六、七十年代提出(这个模型的训练方法由鲍姆的名字命名)。
NLP中,HMM最早应用在语音识别中,后来成功地应用到了机器翻译、拼写纠错、图像处理、基因序列分析等很多问题。
4.1.2 数学角度
目标:给定词串 W = w 1 w 2 … w n W=w1w2…wn W=w1w2…wn、词性标记集TAG,求对应的词性标记串T=t1t2…tn
问题转换为:给定W的条件下,求使得概率P(T|W)最高的那个词性标注串,即 :
T = A r g m a x P ( T i ∣ W ) T = A r g m a x P ( T _ { i } | W ) T=ArgmaxP(Ti∣W)
根据贝叶斯公式:
P ( T ∣ W ) = P ( W ∣ T ) P ( T ) P ( W ) P ( T | W ) = \frac { P ( W | T ) P ( T ) } { P ( W ) } P(T∣W)=P(W)P(W∣T)P(T)
Markov独立性假设:
P ( T ) = P ( t 1 t 2 t 3 ⋯ , t n ) = P ( t 1 ) P ( t 2 ∣ t 1 ) ⋯ P ( t n ∣ t n − 1 ) P ( T ) = P ( t _ { 1 } t _ { 2 } t _ { 3 } \cdots , t _ { n } ) = P ( t _ { 1 } ) P ( t _ { 2 } | t _ { 1 } ) \cdots P ( t _ { n } | t _ { n - 1 } ) P(T)=P(t1t2t3⋯,tn)=P(t1)P(t2∣t1)⋯P(tn∣tn−1)
独立输出假设:
P ( W ∣ T T ) = P ( w 1 w 2 w 3 ⋯ , w n ∣ t 1 t 2 t 3 , ⋯ , t ) = P ( w 1 ∣ t 1 ) P ( w 2 ∣ t 2 ) ⋯ P ( w n ∣ t n ) P ( W | T _ { T } ) = P ( w _ { 1 } w _ { 2 } w _ { 3 } \cdots , w _ { n } | t _ { 1 } t _ { 2 } t _ { 3 , \cdots , t } )=P ( w _ { 1 } | t _ { 1 } ) P ( w _ { 2 } | t _ { 2 } ) \cdots P ( w _ { n } | t _ { n } ) P(W∣TT)=P(w1w2w3⋯,wn∣t1t2t3,⋯,t)=P(w1∣t1)P(w2∣t2)⋯P(wn∣tn)
所以,最终可以得到经典的隐马尔科夫模型:
P ( W ∣ T ) P ( T ) = ∏ i P ( w i ∣ t i ) P ( t i ∣ t i − 1 ) P ( W | T ) P ( T ) = \prod _ { i } P ( w _ { i } | t _ { i } ) P (t _ { i } | t _ { i-1 } ) P(W∣T)P(T)=i∏P(wi∣ti)P(ti∣ti−1)
4.1.3 Maekov模型
现实中经常会出现:一个序列由并不互相独立的随机变量组成,序列中每个变量的值依赖于它前面的元素。如:词串、每天的气温……
但预测将来的依据可能只有有限个随机变量的值而不是前面的所有值。
所以提出Markov假设:序列中未来的元素仅与它前面的一个或几个元素有关,而与其他元素无关。 这是对现实世界的简化:不需要了解序列中所有过去的随机变量值。
如果当前元素的概率只取决于前一个元素,那就叫一阶markov过程
状态转移概率 :
P ( x t ∣ x 1 , x 2 , … , x t − 1 ) = P ( x t ∣ x t − 1 ) P\left(x_{t} \mid x_{1}, x_{2}, \ldots, x_{t-1}\right)=P\left(x_{t} \mid x_{t-1}\right) P(xt∣x1,x2,…,xt−1)=P(xt∣xt−1)
整个序列(Markov链)的概率:
P ( x 1 , x 2 , ⋯ , x T ) = ∏ t = 1 T P ( x t ∣ x t − 1 ) P ( x _ { 1 } , x _ { 2 } , \cdots , x _ { T } ) = \prod _ { t = 1 } ^ { T } P ( x _ { t } | x _ { t - 1 } ) P(x1,x2,⋯,xT)=t=1∏TP(xt∣xt−1)
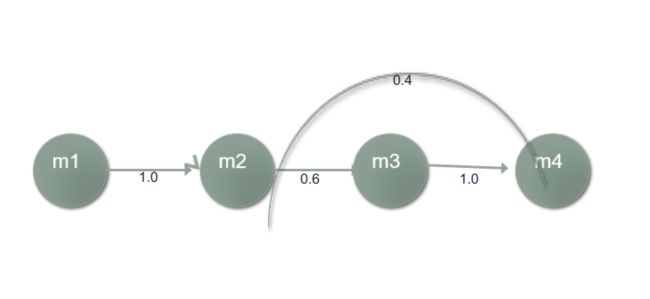
Markov链可以表示状态图、状态转移矩阵。
一个状态图的例子:
4.2 HMM的形式化描述
HMM有两种形式: λ = ( S , O , A , B , π ) λ = ( S, O, A, B, π) λ=(S,O,A,B,π) 或$λ = ( A, B, π) $
4.2.1 几个概率
P ( t i ∣ t i − 1 ) P(t_i|t_{i-1}) P(ti∣ti−1)称为:转移概率
P ( w i ∣ t i ) P(w_i|t_i) P(wi∣ti)称为:发射概率或生成概率(Generation probability),每个隐含状态 t i t_i ti产生相应符号 w i w_i wi的概率。
P ( t i ) P(t_i) P(ti)称为:初始概率
4.2.2 三大问题的解决方案
- 估值问题:给定一个观察序列 O = O 1 O 2 … O T O=O_1O_2…O_T O=O1O2…OT和模型λ,如何计算给定模型λ下观察序列Ο的概率P(O| λ) ? 使用前向算法(forwardalgorithm)
- 解码问题:给定一个观察序列 O = O 1 O 2 … O T O=O_1O_2…O_T O=O1O2…OT,如何决定状态序列 Q = q 1 q 2 … q T Q=q_1q_2…q_T Q=q1q2…qT,使得该状态序列能“最好地解释”观察序列? 使用维特比算法(Viterbialgorithm)
- 学习问题: 给定一个观察序列 O = O 1 O 2 … O T O=O_1O_2…O_T O=O1O2…OT,如何调节λ,使概率P(O| λ)最大 ?使用前向-后向算法(forward-backward algorithm
在词性标注里,我们关注的是解码问题
4.3 参数估计
基于已标注语料库:
-
转移概率
P ( t i ∣ t i − 1 ) = N i m ( t i t i − 1 ) N u m ( t i − 1 ) P ( t _ { i } | t _ { i - 1 } ) = \frac { N _ { i } m ( t _ { i } t _ { i - 1 } ) } { N u m ( t _ { i - 1 } ) } P(ti∣ti−1)=Num(ti−1)Nim(titi−1) -
发射概率
P ( w i ∣ t i ) = N i m ( w i , t i ) N u m ( t i ) P ( w _ { i } | t _ { i } ) = \frac { N _ { i } m ( w _ { i , } t _ { i } ) } { N u m ( t _ { i } ) } P(wi∣ti)=Num(ti)Nim(wi,ti)
-
初始概率(标记 t 1 t_1 t1出现在句首start的概率)
P ( t 1 ∣ S t a r t ) = N i m ( t 1 , S t a r t ) N u m ( S t a r t ) P ( t _ { 1 } | S t a r t ) = \frac { N i m ( t _ { 1 } , S t a r t ) } { N u m ( S t a r t ) } P(t1∣Start)=Num(Start)Nim(t1,Start)
4.4 维特比(viterbi)算法求最大概率
4.4.1 Viterbi算法思想
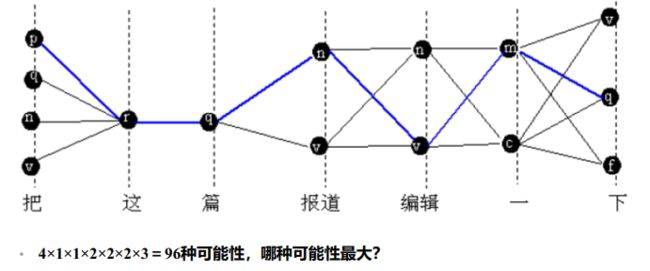
假定有m个词性标记,给定词串中有n个词最坏情况:每个词都有m个可能的词性标记,则可能的状态序列有 m n m^n mn个 ,算法复杂度为指数级,要寻找更高效的算法
所以提出Veterbi算法:一种动态规划方法,把一个复杂问题分解为相对简单的子问题来求解。 对于每个节点,需要知道两个信息:
(1)从起点到达当前节点的累积最大权值为多少;
(2)要达到这个累计最大权值,它的上一个节点是哪一个节点;
可记做: N o d e i ( Σ , N o d e j ) Node_i(Σ, Node_j) Nodei(Σ,Nodej), Σ Σ Σ表示累积最大权值, N o d e j Node_j Nodej表示通向当前节点 N o d e i Node_i Nodei的最佳的上一个节点
所以不难看出,Viterbi的精髓是将全局最佳解分解为阶段最佳解的计算。
4.4.2 Viterbi变量的引入
引入Viterbi变量,记录从起点词到第m个词的第i个词性标记的路径中,概率最大的一条路径,即记录累积最大概率
δ m ( i ) = m a x P ( t 1 , t 2 ⋯ , t m = i , w 1 , w 2 , w m ) \delta_{m} ( i ) = m a x P ( t _ { 1 } , t _ { 2 } \cdots , t _ { m } = i , w _ { 1 } , w _ { 2 } , w _ { m } ) δm(i)=maxP(t1,t2⋯,tm=i,w1,w2,wm)
在终点,可以通过Viterbi变量的回溯,找到最佳路径上的每一个词的最佳词性标记 。Viterbi变量递归求值:
δ m + 1 ( j ) = 1 < = i < v ar m ( i ) P ( t j ) P ( w m + 1 ∣ t j ) \delta_{m+1}( j ) = _ { 1 \lt = i \lt v } \operatorname { a r } _ { m } ( i ) P ( t _ { j } ) P ( w _ { m + 1 } | t _ { j } ) δm+1(j)=1<=i<varm(i)P(tj)P(wm+1∣tj)
4.2.3 算法复杂度
假定有m个词性标记,给定词串中有n个词 ,考虑最坏情况,一个词和前一个词之间有 m 2 m^2 m2种情况,那么算完所有词需要计算 m 2 × ( n − 1 ) m^2\times (n-1) m2×(n−1)次,因为 m m m是已知的,所以复杂度随着词数增加呈现线性增长。
4.2.4 局限性
- 马尔科夫假设对自然语言的刻画太粗糙。
- 如果考虑更多的上下文信息,如:3-gram,4-gram,会造成严重的数据疏问题(0概率问题)。
- 容易训练过度/过拟合(overfitting)
5. 基于转换的词性标注
Transformation-based errordriven part of speech tagging, 1995
• 这个方法名称复杂,但思想非常简单。
• 效果很好,在很多NLP问题上得到了几乎最好的结果。
• 该方法可扩展到无监督学习中
5.1 基本思想
通过不断修正错误得到正确结果 :
- 先简单初标注,如:赋予每个词最常见标记;
- 修正错误,并用转换规则记录修正过程;
- 对学习到的转换规则进行评价,得到排序规则表,选择最有效的规则进行词性标注
5.2 转换规则(改写规则+激活环境)
-
改写规则:将词性标记x改写为y
-
激活环境(触发类型):上下文词性标记、上下文词、其他形态触发 。
上下文窗口大小:考虑了前后各3个词或词性标记
5.3 算法实现
核心:根据错误对比得到转换规则。需要预先确定转换规则的形式,即获取什么样的上下文信息。
规则的评价:利用该规则转换后,语料中的错误数最少(规则是不断变化的)
5.4 算法描述
①首先对 C 0 r a w C_{0_raw} C0raw进行初始标注,得到带有词性标记的语料Ci(i =1);
②将Ci跟正确的语料C0比较,可以得到Ci中总的词性标注错误和候选规则集;
③依次从候选规则集中取出一条规则 T m ( m = 1 , 2 , … ) T_m (m=1,2,…) Tm(m=1,2,…),每用一条规则对Ci中的词性标注结果进行一次修改,就会得到一个新版本的语料库,不妨记做 C i m ( m = 1 , 2 , 3 , … ) C_i^m(m=1,2,3,…) Cim(m=1,2,3,…),将每个 C i m C_i^m Cim跟C0比较,可计算出每个 C i m C_i^m Cim中的词性标注错误数。假定其中错误数最少的那个是 C i j C_i^j Cij(可预期 C i j C_i^j Cij中的错误数一定少于Ci中的错误数),产生它的规则 T j _Tj Tj就是这次学习得到的转换规则;此时 C i j C_i^j Cij成为新的待修改语料库。
④重复第3步的操作,得到一系列的标注语料库C2k, C3l, C4m,…后一个语料库中的标注错误数都少于前一个的错误数,每次都学习到一条令错误数降低最多的转换规则。直至运用所有规则后,都不能降低错误数,学习过程结束。这时得到一个有序的转换规则集合{Ta, Tb,Tc, …}。
5.5 基于转换方法评价
- Brill用这种方法获得的词性标注准确率95.6%,很
多年内无人超越。 - 优势:
- 捕捉了词语和上下文标记之间复杂的依存关系。
- 比HMM利用的信息形式更加丰富,且比概率形式的知识更为简单。
- 所需决策量比HMM中的参数估计少一个数量级
- 几乎不会发生过拟合(overfitting)。
- Brill指出,该方法比决策树学习更强大。
- 代价:
需要搜索一个很大的转换空间,因此需要好的方法来搜索空间 - 与传统规则方法的不同:
- 规则的获取是自动的;
- 规则的覆盖率强;
- 规则的使用有优先级顺序;
- 规则的选择有量化标准
6. 基于分类思想的词性标注
词性标注还可看作一个分类问题:对于句子中的每一个词w,找到一个合适的词类类别t。对于分类问题,有很多现成的数学模型和框架可以套用,如:决策树、最大熵模型、条件随机场、SVM、深度学习模型。
写在最后
词性标注的挑战:新词或未登录词的词性标注
词性标注的新方法:解决序列标注任务常用的深度学习:LSTM+CRF、BiLSTM+CRF 、BERT+CRF等