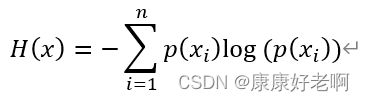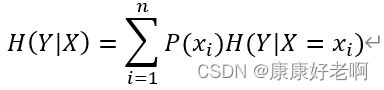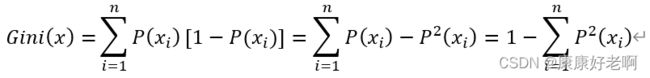机器学习基础自学笔记——决策树(Decision Tree)
决策树(Decision Tree)
目录
决策树(Decision Tree)
信息熵
条件熵
信息增益
基尼系数
决策树主要优缺点：
剪枝处理
随机森林
本文是本人学习决策树时候的笔记，可能很对地方不是比较专业，主要为去理解相关概念为主~
这是我的第一篇博客，若博客有错误欢迎大家指出~
本博客后续也会不断更新~
信息熵
文献参考引用：
· 知乎：忆臻
· 知乎: 林君
· 知乎：许铁-巡洋舰科技
信息熵概念：
信息熵把信息中排除了冗余信息后的平均（有价值）信息。
即 信息就是用来消除人对这件事的不确定性的——消除熵=获取信息
理解：
在化学中我们引入了熵的概念，用于描述体系或者分子的混乱程度。而如果我们拓展这个概念，将熵理解为描述各类事务的一种混乱程度。我们同样也可以将这个概念应用到信息学中。
我们知道信息是一种非常复杂而又不确定的概念。我们难以衡量几千字或者一张图片能 传递给我们多少信息，更不用说其中的有用信息。有用信息往往是要根据实际情况、不 同的人和地点等等复杂因素来衡量的。而信息熵就给我们定义了这样一个抽象概念。
信息熵公式：
理解：
但是通过大量实验以及总结，人们发现往往概率越小的事件发生了那么其价值越高有用信 息越大，而概率越大的事件发生了其有用信息越小。比如，康康小朋友在11.26日晚上吃馒 头作为晚餐，这个一点也不让人奇怪，因为他经常吃；但是哪天他居然一整天呆在宿舍打 游戏，那么闻着可能都会觉得天塌了：怎么可能？？！
所以一个具体事件的信息量应该是随着其发生概率递减的。
假设x,y两个事件没有关系，那么这两个事件得到的信息总和h(xy)
那么他们同时发生的概率P(xy)
而我们又知道，对数的其中一个运算性质为：
我们可以猜出h(x)和p(x)可能会有如下的一种关系（没错，你高考数学选择题的本能）：
（1）其中n一般取2，基于传统的信息论；
（2）由于概率的取值范围是[0,1]，所以为了保证信息量是正数，在log函数前加一个负号。
我们可以简单验证一下：
![h(xy)=-\log_{n}P(xy) =-\log_{n}[P(x)*P(y)] =-\log_{n}P(x)-\log_{n}P(y)=h(x)+h(y)](http://img.e-com-net.com/image/info8/99b6decb98474d949d26a57b61fb0051.gif){kind=small}
没毛病。
对于x这个事件，其发生概率为P(x)，所以其有用信息的期望值为：
而对一个更大的事件A，x事件可能就是其中一个事件，就像买了十根士力架只是出门买零食的一小部分一样。那么总共的有用信息期望值为：
就是对上面式子取了一个求和。
这下我们就得到了一开始给出的公式。
根据我们的推演不难发现，如果一个系统越复杂，出现种类越多，那么他的信息熵越大，纯度越低。这不难理解，当种类多的时候（事件很多），每个种类的概率很小，通过log函数，再加一个负号，就会变得很大
条件熵
条件熵概念：
定义为在X给定条件下，Y的条件概率分布的熵对X的数学期望。数学表达式为 H(Y|X)
理解：
按一个新的变量对原变量进行分类，然后在每个小类里面都计算一个小信息熵（用条件概率），之后求均值。
这样做可以用来判断这个分类标准是否有效，即信息的不确定度是否降低（纯度提高）
如果从树的角度去理解，更加形象但是需要有树的一些基础：
若将信息熵理解为一棵决策树的信息有用程度，其条件就是将根分类出的不同条件。那么 就可以将条件熵理解为这课决策树一棵子树的信息有用程度，而其条件就是决策树子树的 根结点分类出的不同条件，即一个孩子结点。
条件熵公式：
理解：
其实就是将信息熵中的改率换成条件概率，再计算条件概率下的期望值。这样做可以求出 某一事件影响下的信息熵（条件熵）
我们之前学过在事件X的条件下，发生事件Y的条件概率公式：
我们可以用此来帮助理解条件熵的概念（但是数学表达式确实不一样，只能帮助理解“条件”）
定义Y的条件熵 H(Y|X)。这个条件熵也是一个大事件，里面会包含许许多多小事件。类比信息熵的概念，我们会得到：
其中 H(Y|X=xi) 的含义是在xi事件下的信息熵。我们将信息熵公式代入，
根据条件概率公式，p(x)*p(y|x)=p(xy)代入可得
终于到了我们决策树的核心。
构造一棵决策树的想法就是，随着树的深度的增加，结点的熵会迅速降低（有用的信息越来越多，分离得越来越精确）。而我们希望得到一颗熵降低速度最快的一棵决策树，即深度（高度）最小的一棵决策树。因为熵降低越快，树的深度就可以越小，算法更加简单的同时，也减小造成过拟合的可能性。
为了构造这样一个决策树，我们将介绍以下几种算法，帮助我们构造最优化的决策树。
下面介绍的算法分别是信息增益、信息增益率和基尼系数，利用这三个构造损失函数可以帮助我们构造较优的决策树
信息增益——ID3决策树
增益率——C4.5决策树
基尼系数——CART决策树
信息增益
信息增益概念：
信息增益指的是一个特征能为一个分类系统带来多少有用信息。若带来的信息越多，说明该特征越加重要，信息增益也就越大。
信息增益公式：
即用条件熵减去信息熵。
对于多种分类方式，我们通过算法分别计算其信息增益量，选择增益量最大的分类方式作为决策树下一个分类标标准，即分类效果最好的一个标准。这样分类可以使每个类别的信息更纯。
信息增益率：
信息增益率概念：
信息增益率为信息增益量与信息熵的比值。
理解：
在现实生活中，很多的绝对量是没有很大意义的。比如你现在要吐槽你上学期很用功，你说：“我预习了整整五天，我的分数增长了10分！排名上升了2名！”但是问题在于，我根本不知道你是从考1分变成了考11分，排名从全市32651上升到了32649；还是从739分考到了749分，排名从第三名上升到了第一名。至少在我看来，前者的可能性大一些，就算冤枉了你你也别怪我，谁叫你就告诉我哥绝对数字呢。
但是如果我知道的你的排名率（假设我们定义这样一个概念），你告诉我你的排名率是2/32651，或者是2/3，那么我就对你进步的程度有了一些初步的掌握。虽然2/3既可能是从第三名增长到第一名，也有可能是从第150名增长到50名，但是无论哪种情况我都能大概清楚你的进步真的很大（毕竟从第三到第一真的不容易，排名越高越难上升）。【假定这里的排名是综合排名，不考虑偶然性问题】
而信息增益率的作用也是如此。当我们只比较信息增益这一绝对量的时候，其值的大与 小并没有太多的意义，所以我们用比值去定义会更加合理。
信息增益率公式：
基尼系数
基尼系数概念：
基尼系数表示一个集合的不确定性，基尼系数越大，样本的不确定性越大
基尼系数公式：
![Gini(x)=P(x)[1-P(x)]](http://img.e-com-net.com/image/info8/4d6a9ca1ea7f4291bac642f5d2b6ff01.gif){kind=small}
可以理解为将信息熵中的 -log(P(x)) 变换成 1-P(x) ，之后对等式左右两边求和：
理解：
根据这个Gini系数的公式不难发现，当一个事件包含的子事件越多（买零食买得种类特 别多），其每一件事发生的概率越小，即P(x)越小，那么经过平方处理后，这个小于1的 数只会变得更小，而Gini系数会变得更大。使用Gini系数要比信息熵公式更加直观。
决策树主要优缺点：
优点：
-
可同时用于分类和回归任务，且可以处理多分类问题；
-
不需要归一化，减少了数据预处理工作；
-
自动筛选变量，容易解释和可视化决策过程；
-
适合处理高维度数据。
缺点：
-
不稳定，泛化性能差；
-
没有考虑变量之间的相关性，每次筛选都只考虑一个变量；
-
只能线性分割数据；
-
本质上是贪婪算法（可能找不到最优的树）。
剪枝处理
基本概念
根据决策树的原理，如果树的广度和深度过大，分类标准过多，叶子结点过多，容易造成过拟合的现象。下面举一个例子：
假设这是一份关于人们是否选择工作的调查，蓝色的数字表示满足相应的条件的人数。而且我们是将所有情况完全分类的。
但是这时我们出现了另外一个样本，这个样本的情况是这样的：月薪3000~5000元、一周工作5天、年假5~10天、无年终奖，但是他选择接受了这份工作，也就是“Yes”。这个样本就无法被上面的决策树正确预测。
为什么呢？我们注意到月薪3000~5000元、一周工作5天、年假5~10天、无年终奖样本中只有2人，而月薪3000~5000元、一周工作5天、年假5~10天，有年终奖中有31人，我们可以说绝大部分月薪3000~5000元、一周工作5天、年假5~10天的人都会去选择 “Yes” 这个选项。为了这2人单独分出了一个子树虽然使在原有样本中（训练集）的正确率较高，但是泛化（测试集与验证集）程度较差，因为大部分情况都是有年终奖而且选择Yes的人。
但是使用下图的决策树就可以正确预测：
上图将月薪3000~5000元、一周工作5天、年假5~10天、无年终奖样本和有年终奖两个分类合并，也可以进一步合并得到下图：
这两幅图都可以正确预测之前那个样本。虽然这两课决策树对于原有样本（训练集）的准确度降低，但是泛化性增强，提高了预测别的样本（测试集和验证集）的准确度。
而以上这种对决策树的操作称为剪枝处理，形象地可以理解为将决策树的树枝剪掉。这样做可以提高泛化性，更好地去预测别的样本。而剪枝处理也分为两种：预剪枝处理和后剪枝处理。
预剪枝处理
概念：在构建决策树的过程中，提前停止决策树生长。
方法：在构建决策树的过程中，比较划分前后的精确度P，若P变大，则保留该树枝，若P减小或者不变，则丢弃该树枝。
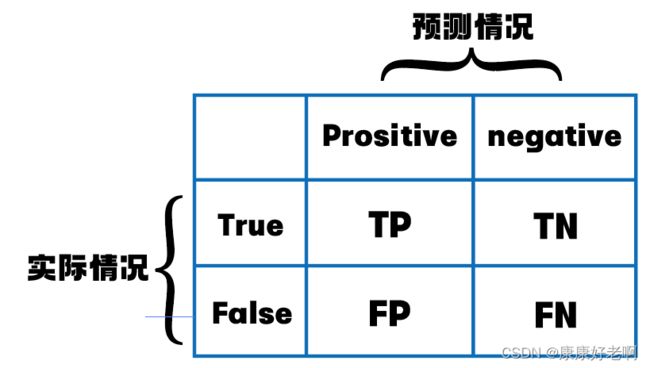
补充：关于精确度Precision的计算和理解
以上是一些常见的概念，下面解释一下：首先我们需要认识到，预测的真假和实际样本的真假是有区别的。为了区分，我们将预测样本为正用Prositive来表示，预测样本为负用Negative来表示；将实际样本为正用True来表示，将实际样本为负用False来表示。正样本指的是属于某一类别的样本，负样本指的是不属于这一类别的样本。
精确度Precision：即在所有预测为正的样本中，实际为正的占比。
召回率Recall：即在所有实际为正的样本中，预测为正的占比。
优点：降低了过拟合风险，同时节约了训练时间
缺点：容易出现欠拟合的问题
后剪枝处理
概念：决策树构建好之后，然后才开始裁剪决策树树枝。
方法：在构建完决策树后，从叶结点开始从下往上比较划分前后的精确度P，若P变大，则保留该树枝，若P减小或者不变，则丢弃该树枝。
优点：欠拟合和过拟合的风险都较低
缺点：训练的时间较长
两种剪枝处理的比较
假设现在我们有一棵如下的完全决策树（将所有情况完全划分，也就是正方形叶子结点的精确度全部为1），其中圆形区域表示分支结点，正方形区域表示叶子结点，结点上的数字表示加入该划分之后的新精确度。
备注：事实上，每个划分前后的精确度并不能用如下图专业的表示，在意义上有些区别，不过利用下图可以较好地帮助我们区分两种剪枝方法。
如果使用预剪枝处理方法，生成的决策树如下图：
如果使用后剪枝处理方法，生成的决策树如下图：
上面两个图对比不难发现，由于预剪枝处理是从上往下，所以只要遇到子树精确度较小就剪去。但是这就可能会带来下面一种情况，就是子树精确度降低，但是子树的子树精确度反而升高（参考完全决策树0.43-0.66-0.76-0.77-0.75-0.98分支），这样直接会造成欠拟合的情况；而后剪枝处理方法虽然可以避免这种情况，但是需要从每个叶子结点回溯比较，时间复杂度要远高于预剪枝处理。
随机森林
随机森林概念
定义：用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。
在正式介绍随机森林之前，我们先简单介绍一下Bagged决策树：
-
从数据集中均匀、有放回的抽取n个训练数据点，作为生成一棵决策树的数据样本；
-
利用这n个样本，训练出一棵决策树；
-
将上述操作重复t次（t也就为决策树的数量）。
于是我们得到了一个由t棵决策树组成的森林。
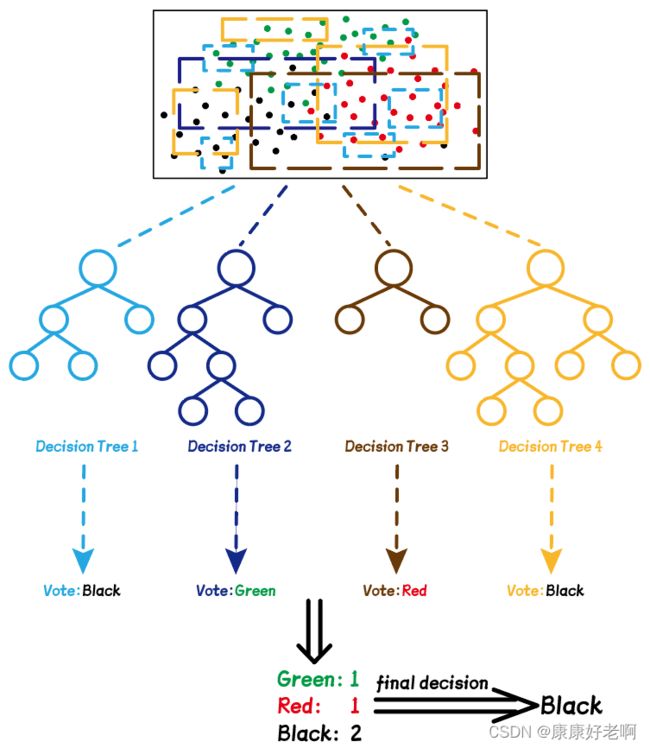
如果我们的树是按照类标签（比如颜色）分类，则最后预测的结果需要采用投票的方式，票数最多的类就是最优的选择。下面是一个举例：
假设我们有如上图的一些数据点，总共三种颜色：红色、黑色和绿色。随机选取样本的过程就像下图一样，随机选取其中一些颜色的点（不一定非要用框框住），不同颜色的框表示不同次选取的点。每次选取的点可以构建一棵决策树（用相应的颜色表示），每个需要预测的点都要由这些决策树“投票”——最后预测的点的颜色为票数最多的点。
上面的Bagged决策树只是对选取的数据点进行了随机，而随机森林中，随机选取的不仅仅是数据点，还有每个数据点的特征。在几乎所有情况下，一个数据拥有的特征都大于1个，在实际工程中，每个数据都拥有成千上万个特征。随机森林通过随机选取这些特征值，可以构造出更多的决策树。
但是随机选取的特征的数量max_feature并不是任意的。如果max_feature过大，则不同决策树之间相似度较高，“投票”的效果降低，受到特殊数据点影响程度较大；如果max_feature过小，则随机森林中的决策树之间差距很大，想要拟合所有数据点必须要用深度很大的决策树。
虽然随机森林中每个决策树都过拟合，但是他们过拟合的方向不同，平均后过拟合程度会大大降低。
随机森林优点：
（1）两个维度的随机性的引入，使随机森林不容易过拟合而且相对其它方法有很好的的抗噪声能力（不容易受到错误数据点的影响）
因为有随机性，所以错误的数据点肯定在随机中会被排除，减小了其对预测的影响
（2）它能够处理很高维度数据，并且不用做特征选择。
（3）对数据集的适应能力强。既能处理离散型数据，也能处理连续型数据
（4）可以得到特征重要性排序以及特征间的相互影响
根据分裂时的信息增益(率)/基尼系数下降量可以判断
随机森林缺点：
（1）训练和预测的速度较慢、而且需要占用大量空间。
最后引用以为知乎答主的文章内容（链接已在文章开头附上）来帮助理解随机森林的作用：
随机森林算法得到的随机森林中的每一棵都是很弱的，但是大家组合起来就很厉害了。我觉得可以这样比喻随机森林算法：每一棵决策树就是一个精通于某一个窄领域 的专家（因为我们从M个feature中选择m让每一棵决策树进行学习），这样在随机森林中就有了很多个精通不同领域的专家，对一个新的问题（新的输入数 据），可以用不同的角度去看待它，最终由各个专家，投票得到结果。而这正是群体智慧——经济学上说的看不见的手，也是这样一个分布式的分类系统，由每一自己子领域里的专家，利用自己独有的默会知识，去对一项产品进行分类，决定是否需要生产。随机森林的效果取决于多个分类树要相互独立，要想经济持续发展，不出现overfiting（就是由政府主导的经济增长，但在遇到新情况后产生泡沫），我们就需要要企业独立发展，独立选取自己的feature 。
欢迎大家关注我哦~
我是爱说自己很老其实不老的康康~