决策树(decision tree)(笔记)
最近在自学图灵教材《Python机器学习基础教程》,在csdn以博客的形式做些笔记。
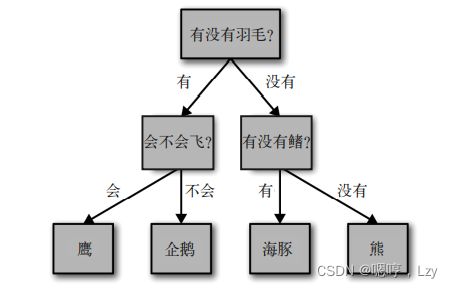
决策树是广泛用于分类和回归任务的模型。本质上,它从一层层的 if/else 问题中进行学习,并得出结论。 想象一下,你想要区分下 面这四种动物:熊、鹰、企鹅和海豚。你的目标是通过提出尽可能少的 if/else 问题来得到 正确答案。你可能首先会问:这种动物有没有羽毛,这个问题会将可能的动物减少到只有 两种。如果答案是“有”,你可以问下一个问题,帮你区分鹰和企鹅。例如,你可以问这 种动物会不会飞。如果这种动物没有羽毛,那么可能是海豚或熊,所以你需要问一个问题 来区分这两种动物——比如问这种动物有没有鳍。 这一系列问题可以表示为一棵决策树。
用机器学习的语言来说就是,为了区分四类动物(鹰、企鹅、海豚和熊),我们利用三个 特征(“有没有羽毛”“会不会飞”和“有没有鳍”)来构建一个模型。我们可以利用监督 学习从数据中学习模型,而无需人为构建模型。
构造决策树
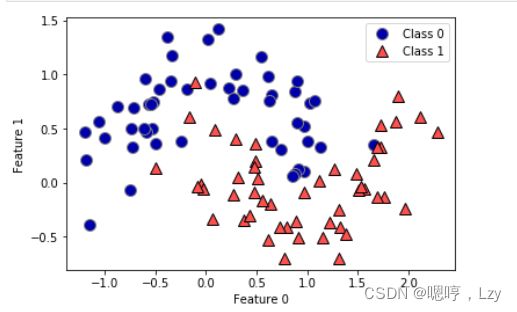
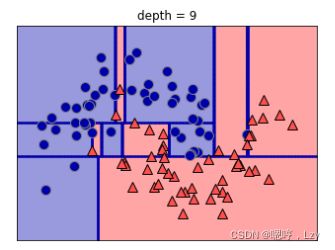
如何构造决策树呢?我们一下面的二维数据集为例,这个数据集由 2 个半月形组成,每个 类别都包含 50 个数据点。我们将这个数据集称为 two_moons。。
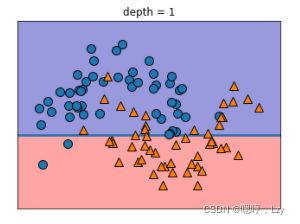
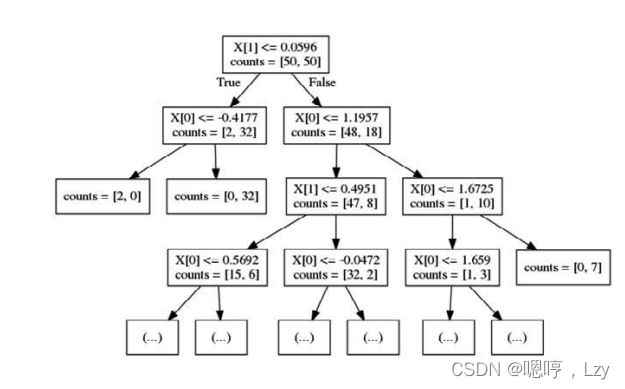
学习决策树,就是学习一系列 if/else 问题,使我们能够以最快的速度得到正确答案。在机器学习中,这些问题叫作测试。 数据通常并不是像动物的例子那样具有二元特征(是 / 否)的形式,而是表示为连续特征。用于连续数据的测试形式是:“特征 i 的值是否大于 a ?”,为了构造决策树,算法搜遍所有可能的测试,找出对目标变量来说信息量最大的那一个。下图展示出了选出的第一个测试,将数据集在 x[1]=0.0596 处垂直划分可以得到最多信 息,它在最大程度上将类别 0 中的点与类别 1 中的点进行区分。顶结点(也叫根结点)表示整个数据集,包含属于类别 0 的 50 个点和属于类别 1 的 50 个点。通过测试 x[1] <= 0.0596 的真假来对数据集进行划分,在图中表示为一条黑线。如果测试结果为真,那么将 这个点分配给左结点,左结点里包含属于类别 0 的 2 个点和属于类别 1 的 32 个点。否则 将这个点分配给右结点,右结点里包含属于类别 0 的 48 个点和属于类别 1 的 18 个点。这两个结点对应于图 2-24 中的顶部区域和底部区域。
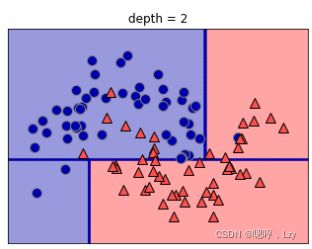
尽管第一次划分已经对两个类别做了很好的区分,但底部区域仍包含属于类别 0 的点,顶部区域也仍包含属于类别 1 的点。我们 可以在两个区域中重复寻找最佳测试的过程,从而构建出更准确的模型。下图展示了信 息量最大的下一次划分,这次划分是基于 x[0] 做出的,分为左右两个区域。
对数据反复进行递归划分,直到划分后的每个区域(决策树的每个叶结点)只包含单一目 标值(单一类别或单一回归值)。如果树中某个叶结点所包含数据点的目标值都相同,那 么这个叶结点就是纯的(pure)。最终划分结果如下图所示。
想要对新数据点进行预测,首先要查看这个点位于特征空间划分的哪个区域,然后将该区域的多数目标值(如果是纯的叶结点,就是单一目标值)作为预测结果。从根结点开始对树进行遍历就可以找到这一区域,每一步向左还是向右取决于是否满足相应的测试。 决策树也可以用于回归任务,使用的方法完全相同。预测的方法是,基于每个结点的测试对树进行遍历,最终找到新数据点所属的叶结点。这一数据点的输出即为此叶结点中所有训练点的平均目标值。
控制决策树复杂度
如果要构造决策树直到所有叶结点都为纯叶结点,则会使得模型极为复杂,并且对训练集高度过拟合。 从上述数据集的最终划分结果可以看出,属于类别0的点中间有一块属于类别1的区域,同时有一小条属于类别 0 的区域,包围着最右侧属于类别 0 的那个点。这并不是我们想要的决策边界,因为它过于关注单个异常点了。
为了防止过拟合,我们可以采用预剪枝(及早停止树的生长)和后剪枝(先构造树,但随后删除或折叠信息量很少的结点,有的书上也称之为剪枝);预剪枝的限制条件可能包括限制树的最大深度、限制叶结点的最大数目, 或者规定一个结点中数据点的最小数目来防止继续划分。
在scikit-learn中只实现了预剪枝,并未实现后剪枝,所以我们只讨论预剪枝
预剪枝
我们在将官方给的乳腺癌数据集上更详细地看一下预剪枝的效果。
我们先不进行预剪枝:
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split( cancer.data, cancer.target,stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))训练集上的精度是 100%,这是因为叶结点都是纯的,树的深度很大,足以完 美地记住训练数据的所有标签。测试集精度比线性模型略低,线性模型的精度约为 95%,感兴趣的小伙伴可以使用线性模型跑一下数据。
现在我们将预剪枝应用在决策树上,这可以在完美拟合训练数据之前阻止树的展开。一种选择是在到达一定深度后停止树的展开。这里我 们设置 max_depth=4,这意味着只可以连续问 4 个问题。限制树的深度可以减少过拟合。这会降低训练集的精度,但可以提高测试集的精度:
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))分析决策树
我们可以利用 tree 模块的 export_graphviz 函数来将树可视化。这个函数会生成一 个 .dot 格式的文件,这是一种用于保存图形的文本文件格式。我们设置为结点添加颜色 的选项,颜色表示每个结点中的多数类别,同时传入类别名称和特征名称,这样可以对树正确标记:
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["malignant","benign"],
feature_names=cancer.feature_names, impurity=False, filled=True)我们可以利用 graphviz 模块读取这个文件并将其可视化
import graphviz
with open("tree.dot") as f:
dot_graph = f.read()
graphviz.Source(dot_graph)(图太大了只能截取大部分)
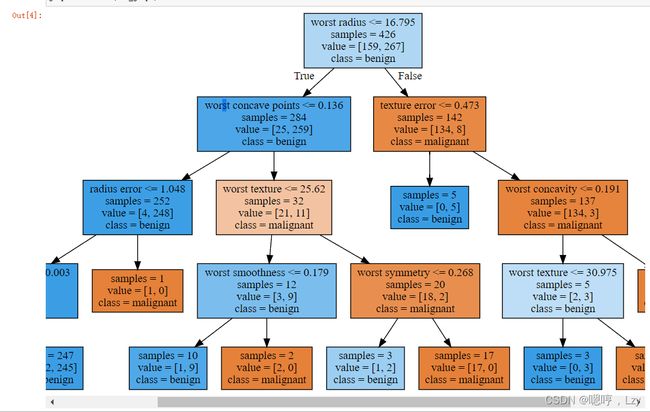
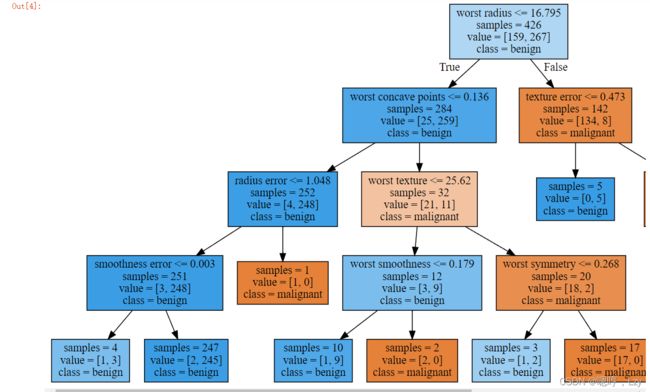
树的可视化有助于深入理解算法是如何进行预测的,也是易于向别人解释的机器学习算法的优秀示例。不过,即使这里树的深度只有 4 层,也有点太大了。深度更大的树更加难以理解。一种观察树的方法可能有用,就是找出大部分数据的实际路径。
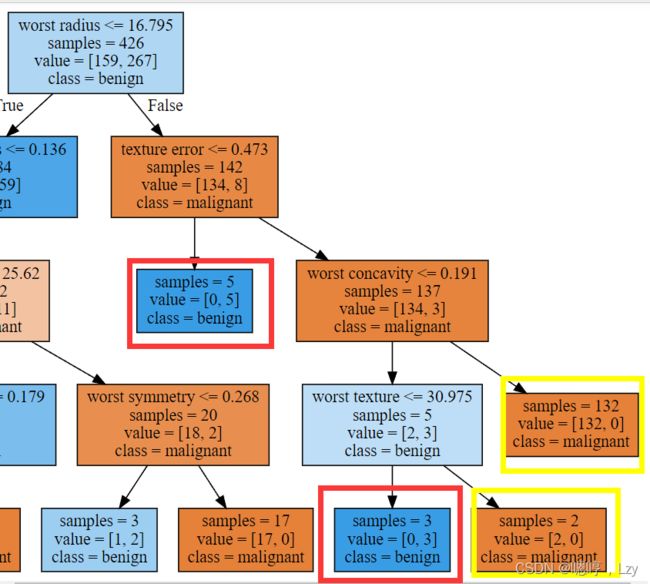
观察 worst radius <= 16.795 分支右侧的子结点,我们发现它只包含 8 个良性样本,但有 134 个恶性样本。树的这一侧的其余分支只是利用一些更精细的区别 将这 8 个良性样本分离出来。在第一次划分右侧的 142 个样本中,几乎所有样本(132 个) 最后都进入最右侧的叶结点中。
再来看一下根结点的左侧子结点,对于 worst radius > 16.795,我们得到 25 个恶性样本 和 259 个良性样本。几乎所有良性样本最终都进入左数第二个叶结点中,大部分其他叶结点都只包含很少的样本。
树的特征重要性
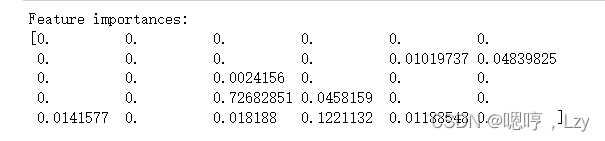
查看整个树可能非常费劲,除此之外,我还可以利用一些有用的属性来总结树的工作原 理。其中最常用的是特征重要性(feature importance),它为每个特征对树的决策的重要性 进行排序。对于每个特征来说,它都是一个介于 0 和 1 之间的数字,其中 0 表示“根本没 用到”,1 表示“完美预测目标值”。特征重要性的求和始终为 1。
接下来让我们看一看上述乳腺癌数集决策树模型的特征重要性
print("Feature importances:\n{}".format(tree.feature_importances_))我们可以将其可视化:
import numpy as np
import matplotlib.pyplot as plt
def plot_feature_importances_cancer(model):
n_features = cancer.data.shape[1]
plt.barh(np.arange(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
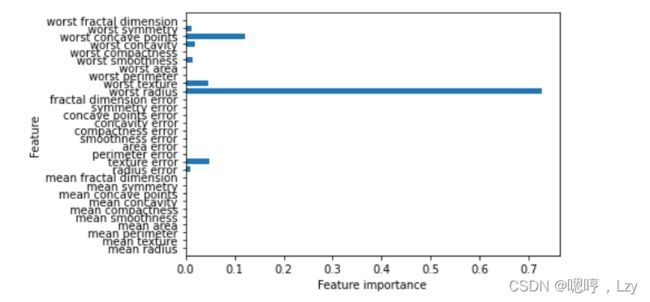
plot_feature_importances_cancer(tree)这里我们看到,顶部划分用到的特征(“worst radius”)是最重要的特征。这也证实了我们 在分析树时的观察结论,即第一层划分已经将两个类别区分得很好。 但是,如果某个特征的 feature_importance_ 很小,并不能说明这个特征没有提供任何信 息。这只能说明该特征没有被树选中,可能是因为另一个特征也包含了同样的信息。
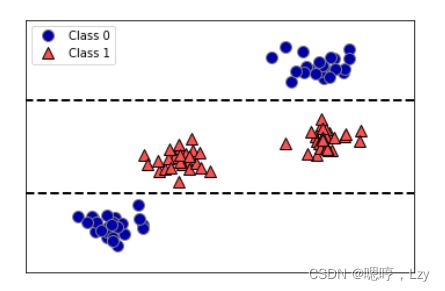
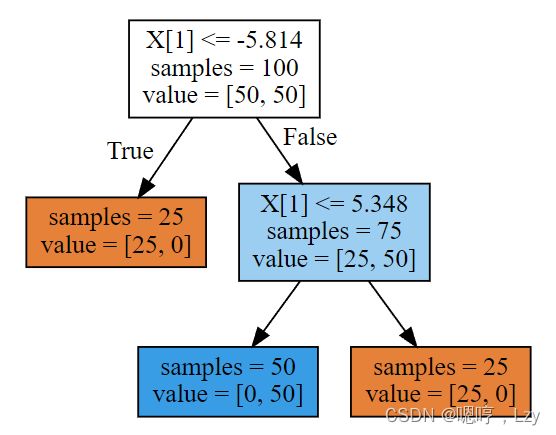
与线性模型的系数不同,特征重要性始终为正数,也不能说明该特征对应哪个类别。特征 重要性告诉我们“worst radius”(最大半径)特征很重要,但并没有告诉我们半径大表示 样本是良性还是恶性。事实上,在特征和类别之间可能没有这样简单的关系,你可以在下 面的例子中看出这一点:
该图显示的是有两个特征和两个类别的数据集。这里所有信息都包含在 X[1] 中,没有用到 X[0]。但 X[1] 和输出类别之间并不是单调关系,即我们不能这么说:“较大的 X[1] 对应类 别 0,较小的 X[1] 对应类别 1”。
优缺点
优点:决策树有两个优点:一是得到的模型很容易可视化,非 专家也很容易理解(至少对于较小的树而言);二是算法完全不受数据缩放的影响。由于 每个特征被单独处理,而且数据的划分也不依赖于缩放,因此决策树算法不需要特征预处 理,比如归一化或标准化。特别是特征的尺度完全不一样时或者二元特征和连续特征同时 存在时,决策树的效果很好。
缺点:决策树的主要缺点在于,即使做了预剪枝,它也经常会过拟合,泛化性能很差。因此,在 大多数应用中,往往使用集成方法来替代单棵决策树,如随机森林,梯度提升回归树。