研究生工作周报(第六周)
学习目标:
- 机器学习总结
- 深度学习第四课《卷积神经网络》-Stanford吴恩达教授
- "花书"第一部分第五章机器学习基础
学习内容:
- 像素填充padding
- 卷积步长 (Strided Convolutions)
- 三维卷积 (Convolutions Over Volumes)
- 池化层 (Pooling Layers)
- 残差网络 (Residual Networks (ResNets))
学习时间:
- 6.12~6.18
学习产出:
- 学习总结1篇
- github仓库
Padding
为了构建深度神经网络,需要学会使用的一个基本的卷积操作就是padding。如果用一个3×3的过滤器卷积一个6×6的图像,你最后会得到一个4×4的输出,也就是一个4×4矩阵。
数学解释:
如果我们有一个 n ∗ n n ∗ n n∗n 的图像,用 f ∗ f f ∗ f f∗f的过滤器做卷积,那么输出的维度就是 ( n − f + 1 ) ∗ ( n − f + 1 ) ( n − f + 1 ) ∗ ( n − f + 1 ) (n−f+1)∗(n−f+1)。
Padding的两个缺点:
1)输出缩小:每次做卷积操作,你的图像就会缩小
2)边缘信息丢失:图像边缘像素点只被一个输出所触碰或者使用
我们可以选择在边缘填充像素来弥补Padding卷积的缺陷,根据填充的像素层数 p p p又可分为Valid卷积和Same卷积,其中Valid卷积意味着不填充,Same卷积填充的像素层数 p p p使得输入输出大小相同。
Valid:
有一个 n ∗ n n ∗ n n∗n的图像,用一个 f ∗ f f ∗ f f∗f的过滤器卷积,它将会给你一个 ( n − f + 1 ) ∗ ( n − f + 1 ) ( n − f + 1 ) ∗ ( n − f + 1 ) (n−f+1)∗(n−f+1)维的输出。
Same:
有一个 n ∗ n n ∗ n n∗n 的图像,用 p p p个像素填充边缘,输出的大小就是这样的 ( n + 2 p − f + 1 ) ∗ ( n + 2 p − f + 1 ) ( n + 2 p − f + 1 ) ∗ ( n + 2 p − f + 1 ) (n+2p−f+1)∗(n+2p−f+1),欲使图像大小不变,即 n + 2 p − f + 1 = n n + 2 p − f + 1 = n n+2p−f+1=n可解得 p = ( f − 1 ) / 2 p = ( f − 1 ) / 2 p=(f−1)/2
在计算机视觉中,通常采用 f f f为奇数过滤器,此时Same卷积可以自然填充,偶数过滤器通常会有一些不均匀填充现象,且奇数过滤器另一个优势在于有一个中心像素点会更方便指出过滤器的位置。
卷积步长
即每次让过滤器跳过s个步长。
如果你用一个 f ∗ f f ∗ f f∗f的过滤器卷积一个 n ∗ n n ∗ n n∗n的图像,你的padding为 p p p ,步幅为 s s s,(现在不是一次移动一个步子,而是一次移动 s s s个步子)输出于是变为 ( n + 2 p − f s + 1 ) ∗ ( n + 2 p − f s + 1 ) (\frac{n+2p-f}{s}+1)*(\frac{n+2p-f}{s}+1) (sn+2p−f+1)∗(sn+2p−f+1)。当尚不为整数时向下取整。

三维卷积
当我们想检测RGB彩色图像的特征时,例如一个彩色图像如果是6×6×3,这里的3指的是三个颜色通道,可以把它看成三个6×6图像的堆叠。为了检测图像的边缘或者其他的特征,不是把它跟原来的3×3的过滤器做卷积,而是跟一个三维的过滤器,它的维度是3×3×3,这样这个过滤器也有三层,对应红绿、蓝三个通道。

总结一下维度,如果你有一个 n ∗ n ∗ n c n*n*n_c n∗n∗nc(通道数)的输入图像,在这个例子中就是6×6×3,然后卷积上一个 f ∗ f ∗ n c f*f*n_c f∗f∗nc ,这个例子中是3×3×3,按照惯例,通道数 n c n_c nc必须数值相同。然后你就得到了 ( n − f + 1 ) ∗ ( n − f + 1 ) ∗ n c ′ ( n-f+1 )∗( n-f+1)∗n_{c^{'}} (n−f+1)∗(n−f+1)∗nc′,这里 n c ′ n_{c^{'}} nc′ 其实就是下一层的通道数,它就是你用的过滤器的个数,在这个例子是4×4×2。(如果你用了不同的步幅 s s s或者padding,那么这个 n − f + 1 n − f + 1 n−f+1数值会变化)。
池化层
卷积神经网络通常使用池化层来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性。
最大池化直观理解:把输入拆分成不同的区域,把这个区域用不同颜色来标记。输出的每个元素都是其对应颜色区域中的最大元素值。
残差网络
非常非常深的神经网络是很难训练的,因为存在梯度消失和梯度爆炸问题。这节课我们学习跳跃连接(Skip connection),它可以从某一层网络层获取激活,然后迅速反馈给另外一层,甚至是神经网络的更深层。我们可以利用跳跃连接构建能够训练深度网络的ResNets。

每两层增加一个捷径,构成一个残差块。如图所示,5个残差块连接在一起构成一个残差网络。
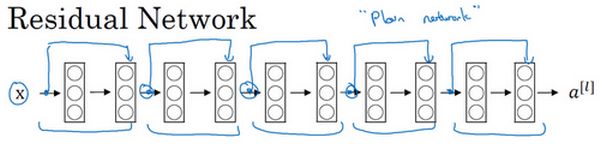
如果我们使用标准优化算法训练一个普通网络,比如说梯度下降法,或者其它热门的优化算法。如果没有残差,没有这些捷径或者跳跃连接,凭经验你会发现随着网络深度的加深,训练错误会先减少,然后增多。而理论上,随着网络深度的加深,应该训练得越来越好才对。也就是说,理论上网络深度越深越好。但实际上,如果没有残差网络,对于一个普通网络来说,深度越深意味着用优化算法越难训练。实际上,随着网络深度的加深,训练错误会越来越多。
总结
《机器学习实战》一书基本看完,关于机器学习的内容也专研了一个多月,包括一些基本概念,各种分类聚类算法的原理,课本示例代码的练习,部分算法的完整复现,掌握了一些像如何进行误差分析,改善模型表现的基本机器学习策略,看到书后半部分的关联规则挖掘算法Apriori和频繁模式树算法FP-growth,体会到了复合算法设计的巧妙之处,还有很多地方需要细细琢磨,这周由于时间问题没有进行太多新的东西,主要是总结机器学习的内容,结合《深度学习》第一部分应用数学与机器学习基础复习巩固。
视频课程的话主要抽工作日零碎时间看的《卷积神经网络》部分,总结的还不是太完善,这周末会继续补充。
这周末陈教授将推荐新的老师,结合老师下一步安排规划后续学习。