【数据结构】波兰式、逆波兰式与中缀表达式

目录

• 中缀表达式
• 后缀表达式
• 前缀表达式
• 计算后缀表达式结果
• 计算机实现中缀转后缀

中缀表达式

 中缀表达式即运算符在操作数之间的表达式，常见表达式均为中缀表达式。因为中缀表达式更利于人们理解以及计算，但中缀表达式却并不利于计算机进行计算。常见算式由操作数、运算符以及界限符组成，例如：
$$\left(\left(15÷\left(7-\left(1+1\right)\right)\right)\times 3\right)-\left(2+\left(1+1\right)\right)$$
可以发现界限符()以及运算符优先级控制着中缀表达式的运算顺序。

后缀表达式

后缀表达式也叫逆波兰式，于1924年由波兰数学家提出。逆波兰式可以在没有界限符的情况下无歧义的计算表达式的值。
中缀转后缀的手算过程：

1、确定中缀表达式各个运算符的运算顺序；
2、选择下一个运算符，按照【左操作数 右操作数 运算符】的次序组合出一个新的操作数；
3、如果还有操作数没有选取继续操作2。

对于$a+b\times \left(c-d\right)-e÷f$其运算顺序以及各步骤对应后缀表达式为：
1、$\left(c-d\right)$
后缀表示为：$cd-$
2、$b\times \left(c-d\right)$
后缀表示为：$bcd-\ast$
3、$e÷f$
后缀表示为：$ef÷$
4、$a+b\times \left(c-d\right)$
后缀表示为：$abcd-\ast +$
5、$a+b\times \left(c-d\right)-e÷f$
后缀表示为：$abcd-\ast +ef÷-$

前缀表达式

 前缀表达式也叫波兰式，于1924年由波兰数学家提出。同逆波兰式可以在没有界限符的情况下无歧义的计算表达式的值。
中缀转前缀的手算过程，二者的计算几乎完全相同：

1、确定中缀表达式各个运算符的运算顺序；
2、选择下一个运算符，按照【运算符 左操作数 右操作数】的次序组合出一个新的操作数；
3、如果还有操作数没有选取继续操作2。

对于$a+b\times \left(c-d\right)-e÷f$其运算顺序以及各步骤对应后缀表达式为：
1、$\left(c-d\right)$
后缀表示为：$-cd$
2、$b\times \left(c-d\right)$
后缀表示为：$\ast b-cd$
3、$e÷f$
后缀表示为：$÷ef$
4、$a+b\times \left(c-d\right)$
后缀表示为：$+a\ast b-cd$
5、$a+b\times \left(c-d\right)-e÷f$
后缀表示为：$-+a\ast b-cd÷ef$

注意：前缀表达式作用同后缀表达式，且一般后缀表达式更常用，并且二者可以做到知其一而融汇贯通的效果。因此下文着重对后缀表达式展开讲述。

计算后缀表达式结果

$\left(\left(15÷\left(7-\left(1+1\right)\right)\right)\times 3\right)-\left(2+\left(1+1\right)\right)$的后缀表示式为15 7 1 1 + -$÷$ 3 $\times$ 2 1 1 + + -
后缀表达式的手算结果步骤：

1、从左往右扫描操作符
2、使用遇到操作符前面的两个操作数计算并生成一个新的操作数
3、还有操作符时继续执行第2部

15 7 1 1 + -$÷$ 3 $\times$ 2 1 1 + + - 的计算过程(用括号说明计算顺序)：
1、15 7 (1 1 +) -$÷$ 3 $\times$ 2 1 1 + + - 此时(1 1 +)结合得到新操作数2后缀表达式转化为：
$$1572-÷3\times 211++-$$
2、15 (7 2 -)$÷$ 3 $\times$ 2 1 1 + + - 此时(7 2 -)结合得到新操作数5后缀表达式转化为：
$$155÷3\times 211++-$$
3、(15 5$÷$) 3 $\times$ 2 1 1 + + - 此时(15 5$÷$) 结合得到新操作数3后缀表达式转化为：
$$33\times 211++-$$
4、(3 3 $\times$) 2 1 1 + + - 此时(3 3 $\times$ ) 结合得到新操作数9后缀表达式转化为：
$$9211++-$$
5、9 2 (1 1 +) + - 此时(1 1 + ) 结合得到新操作数2后缀表达式转化为：
$$922+-$$
6、9 (2 2 +) - 此时(2 2 + ) 结合得到新操作数4后缀表达式转化为：
$$94-$$
7、9 4 - 此时(9 4 - ) 结合得到新操作数5即为最终计算结果

 很容易发现这个过程可以使用数据结构栈来辅助完成，因为操作数的使用顺序满足后进先出的性质。每次遇到操作符时从操作数栈弹出两个数字并运算，将运算得到的新操作数压入栈中。

后缀表达式的机算结果步骤：

1、从左往右扫描元素直到处理至最后一个元素；
2、每当扫描到操作数时将其压入操作数栈，扫描到操作符时从操作数栈中弹出两个元素并按照后弹出操作数为操作数1计算结果并压入操作数栈。

计算过程与手算过程几乎完全相同，不过多演示

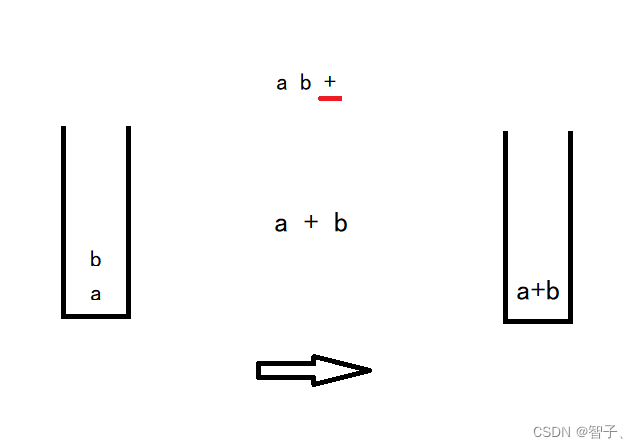
由后缀表达式计算最终结果：

double caculate(string pos)
{
	stack<double> s;
	for (int i = 0; pos[i]; ++i) {
		if (pos[i] == ' ') continue; // 兼容包含多余空格的字符串
		if (isdigit(pos[i])) { // 操作数直接压入栈中
			int j = i;
			bool flag = 1;
			while (isdigit(pos[j + 1]) || (pos[j + 1] == '.' && flag)) { // 找出操作数所在子串，并兼容了小数
				if (pos[j + 1] == '.') flag = 0;
				j++;
			}
			string num = pos.substr(i, j - i + 1);
			s.push(stod(num));
			i = j;
		} else { // 遇到操作符：从操作数栈中弹出两个元素并按照后弹出操作数为操作数1计算结果并压入操作数栈
			double b = s.top(), a;
			s.pop();
			a = s.top();
			s.pop();
			switch (pos[i]) {
			case '+': 
				s.push(a + b);
				break;
			case '-':
				s.push(a - b);
				break;
			case '*':
				s.push(a * b);
				break;
			case '/':
				if (b == 0) return -1; // 除数为0异常
				s.push(a / b);
				break;
			}
		}
	}
	return s.size() == 1 ? s.top() : -1; // 后缀表达式不合法异常
}

计算机实现中缀转后缀

 首先，初始化一个栈用于保存暂时不能确定运算顺序的运算符。然后从左往右扫描，此时会遇到三种情况：

1、遇到操作数。直接加入后缀表达式；
2、遇到界限符。遇到‘(’直接入栈；遇到‘)’依次弹出栈内运算符并加入后缀表达式，直到弹出‘(’为止，注意‘(’不需要加入后缀表达式；
3、遇到运算符。依次弹出栈内优先级高于或等于当前运算符的所有运算符，并加入后缀表达式，若碰到‘(’或栈空则停止；
4、扫描结束时将栈内所有运算符依次弹出。

让我们分析以下这样做的原因：

1、运算符处理。手算后缀表达式时第一步要先确定各个运算符的运算顺序，因此每次遇到运算符时应等待后续运算符才能确定当前运算符是否优先级高于后续运算符(例如：a + b / c);

2、界限符处理。界限符本质上就是一个独立的表达式，其计算结果就是一个操作数。因此，界限符内部的算式可以按一般算式展开，界限符分隔出了一个单独的表示式。

根据上述描述与分析得到能够将中缀表达式字符串转换为后缀表达式字符串的函数：

/*
参数
	中缀表达式 如：12 + 13 * (14.5 - 15) - 16 / 17
返回值
	后缀表达式 如：12 13 14.5 15 - * + 16 17 / -
*/
string mid_trans_pos(string mid)
{
	string pos = "";
	stack<char> s;
	for (int i = 0; mid[i]; ++i) {
		if (mid[i] == ' ') continue; // 兼容包含多余空格的字符串
		if (isdigit(mid[i])) { // 扫描到操作数
			int j = i;
			bool flag = 1;
			while (isdigit(mid[j + 1]) || (mid[j + 1] == '.' && flag)) { // 找出操作数所在子串，并兼容了小数
				if (mid[j + 1] == '.') flag = 0;
				j++;
			}
			string num = mid.substr(i, j - i + 1);
			pos += num + " ";
			i = j;
		} else if (mid[i] == '(' || mid[i] == ')') { // 扫描到界限符
			if (mid[i] == '(') {
				s.push(mid[i]);
			} else {
				while (!s.empty()) {
					if (s.top() == '(') {
						s.pop();
						break;
					}
					pos += s.top();
					pos += " ";
					s.pop();
				}
			}
		} else { // 扫描到操作符
			while (!s.empty()) {
				if (mid[i] == '+' || mid[i] == '-') {
					if (s.top() == '(') {
						s.pop();
						break;
					}
				} else {
					if (s.top() == '(') {
						s.pop();
						break;
					} else if (s.top() == '+' || s.top() == '-') {
						break;
					}
				}
				pos += s.top(); 
				pos += " ";
				s.pop();
			}
			s.push(mid[i]);
		}
	}
	while (!s.empty()) { // 最后将剩余操作符放置末尾
		pos += s.top();
		pos += " ";
		s.pop();
	}
	return pos;
}

相关测试及输出：

12 + 13 * (14.5 - 15) - 16 / 17
12 13 14.5 15 - * + 16 17 / -

结合之前的后缀表达式求值函数caculate(pos)得到计算结果：

/*
int main()
{
	string s;
	getline(cin, s);
	cout << mid_trans_pos(s) << endl;
	cout << caculate(mid_trans_pos(s)) << endl;
	return 0;
}
*/
12 + 13 * (14.5 - 15) - 16 / 17
12 13 14.5 15 - * + 16 17 / -
4.55882

但其实中缀转后缀并求结果可以同步进行，因为每当操作符的计算生效顺序确定时就可以进行计算。因此可以得到以下更为简介的程序：

double result(char op, stack<double>& s) 
{
	double ans = 0, b = s.top(), a;
	s.pop();
	a = s.top();
	s.pop();
	switch (op) {
	case '+':
		ans = a + b;
		break;
	case '-':
		ans = a - b;
		break;
	case '*':
		ans = a * b;
		break;
	case '/':
		if (b == 0) return -1; // 除数为0异常
		ans = a / b;
		break;
	}
	return ans;
}

/*
参数
中缀表达式 如：12 + 13 * (14.5 - 15) - 16 / 17
返回值
中缀表达式计算结果 如：4.55882
*/
double transAndcaculate(string mid)
{
	stack<char> op; // 操作符栈，用于辅助确定操作符的生效顺序
	stack<double> number; // 操作数栈
	for (int i = 0; mid[i]; ++i) {
		if (mid[i] == ' ') continue; // 兼容包含多余空格的字符串
		if (isdigit(mid[i])) { // 扫描到操作数
			int j = i;
			bool flag = 1;
			while (isdigit(mid[j + 1]) || (mid[j + 1] == '.' && flag)) { // 找出操作数所在子串，并兼容了小数
				if (mid[j + 1] == '.') flag = 0;
				j++;
			}
			string num = mid.substr(i, j - i + 1);
			number.push(stod(num)); // 操作数压入栈中
			i = j;
		}
		else if (mid[i] == '(' || mid[i] == ')') { // 扫描到界限符
			if (mid[i] == '(') {
				op.push(mid[i]);
			} else {
				while (!op.empty()) {
					if (op.top() == '(') {
						op.pop();
						break;
					}
					number.push(result(op.top(), number)); // 每当操作符的计算生效顺序确定时就可以进行计算
					op.pop();
				}
			}
		}
		else { // 扫描到操作符
			while (!op.empty()) {
				if (mid[i] == '+' || mid[i] == '-') {
					if (op.top() == '(') {
						op.pop();
						break;
					}
				} else {
					if (op.top() == '(') {
						op.pop();
						break;
					}
					else if (op.top() == '+' || op.top() == '-') {
						break;
					}
				}
				number.push(result(op.top(), number)); // 每当操作符的计算生效顺序确定时就可以进行计算
				op.pop();
			}
			op.push(mid[i]);
		}
	}
	while (!op.empty()) { // 剩余操作符生效顺序确定可以进行计算
		number.push(result(op.top(), number));
		op.pop();
	}
	return number.size() == 1 ? number.top() : -1; // 中缀表达式不合格异常
}