不同图像的噪声，选用什么滤波器去噪，图像处理的噪声和处理方法

不同图像的噪声，选用什么滤波器去噪，图像处理的噪声和处理方法

提示：据说是科大讯飞的算法面试题

知道哪些噪声，分别用什么滤波器处理？

---

图像噪声

噪声来源灰常多，但主要可以分为三类：

1.来自捕捉源的（acquisition/digitization），比如一个摄像机的镜头、A/D或者sensor；

2.来自图像传输过程（image transmission），传输图像的信道包括无线电、微波、光缆等等，如果通过无线电传输，遇到个风吹雨雪的，自然会有各种噪声了；

3.来自计算过程（computation），比如咱们将浮点型数据转化为整形处理，就会丢失部分信息，但这不属于错误，是把问题简化，所以这也是一种噪声。

所以，图像复原主要是用各种滤波方法去除噪声。

因为噪声的来源飘忽不定，所以噪声的种类很多。
包括
指数噪声（exponential noise）、
均匀噪声（uniform noise）、
脉冲噪声（impulse noise）、
椒盐噪声（salt and pepper noise）（也叫黑白噪声，就是黑白点）、
斑点噪声（speckle noise）（大多在雷达信号里产生）、
瑞利噪声（reyleigh noise）（不太明白这种噪声的来源）、
周期噪声（periodic noise）。

而在一般不知道噪声属于什么类型时，多加入高斯噪声进行模拟。

针对不同噪声选用不同滤波器效果也不同。
常见的处理方法：均值滤波 、中值滤波、高斯滤波、双边滤波器去噪 双边滤波

椒盐噪声与中值滤波去噪

首先，对lena女神加入椒盐噪声，因为椒盐噪声为黑白噪声，所以中值滤波效果应该不错。
试验结果如下图：

加椒盐噪声

用中值滤波去噪：

 
Image image = Image.FromFile("xx.jpg");
Image<Bgr, byte> img = new Image<Bgr, byte>((Bitmap)image);//实例化一个三通道的OPENCV的图像对象
Int k=3;//滤波核，奇数
 img =img.SmoothMedian(k);//按照指定的滤波核进行中值滤波
Bitmap bitmap= img.Bitmap;//输出Bitmap格式的结果

经过中值滤波，基本恢复原始图像

均值滤波

 
Image image = Image.FromFile("xx.jpg");
Image<Bgr, byte> img = new Image<Bgr, byte>((Bitmap)image);//实例化一个三通道的OPENCV的图像对象
Int k=3;//滤波核，奇数
img = img. SmoothBlur (k,k);//按照指定的滤波核进行均值滤波
Bitmap bitmap= img.Bitmap;//输出Bitmap格式的结果

---

高斯噪声与高斯滤波去噪

再对原始图像加入高斯噪声。

因为高斯噪声的范围遍布所有灰度级，所以，任何一种低通、高通、带通滤波器都无法完全将其滤除，我们只能尽可能的获得较好效果。
经过查资料，滤除高斯噪声的主要方法有：
平滑线性滤波、
高斯滤波、
维纳滤波还有
小波去噪（小波去噪有些复杂，今天没做）。

下图是加入高斯噪声的效果。

加高斯噪声

下面分别是针对高斯噪声，采用平滑线性滤波、高斯滤波、维纳滤波处理的直观效果。



直观上看平滑线性滤波没有高斯滤波和维纳滤波效果好。

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，普遍应用于图像处理的减噪过程。

高斯滤波就是对整幅图像进行加权平均的过程，每个像素点的值，
都由其自己和邻域内的其余像素值通过加权平均后获得。

高斯滤波的具体操做是：用一个模板（或称卷积、掩模）扫描图像中的每个像素，
用模板肯定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

双边滤波器去噪

双边滤波器（Bilateral filter）是一种能够保边去噪的滤波器。

能够滤除图像数据中的噪声，且还会保留住图像的边缘、纹理等
（因噪声是高频信号，边缘、纹理也是高频信息，
高斯滤波会在滤除噪声的同时使得边缘模糊）。

是使用一个卷积核（模板矩阵），叠加到待处理像素点上，
使用对应邻域像素点的加权求和来做为新的输出像素点的值一种方法，
简单来讲，双边滤波和高斯滤波同样，不一样只在于模板矩阵的不一样。

 
Image image = Image.FromFile("xx.jpg");
Image<Bgr, byte> img = new Image<Bgr, byte>((Bitmap)image);//实例化一个三通道的OPENCV的图像对象
Int k=3;//滤波核，奇数
CvInvoke.EdgePreservingFilter(img, img, EdgePreservingFilterFlag.NormconvFilter, k, 0.4f);;//按照指定的滤波核进行双边滤波
Bitmap bitmap= img.Bitmap;//输出Bitmap格式的结果

小波去噪

将信号经过小波变换（采用Mallat算法）后，
信号产生的小波系数含有信号的重要信息
，将信号经小波分解后小波系数较大，噪声的小波系数较小，

而且噪声的小波系数要小于信号的小波系数，
经过选取一个合适的阀值，大于阀值的小波系数被认为是有信号产生的，应予以保留，
小于阀值的则认为是噪声产生的，置为零从而达到去噪的目的。

离散余弦变换DCT滤波

时间域相对于空间域增加了一个时间维度，
可以对不同时间段的图像进行处理，
对时域噪声有很好的抑制作用。

而频率域又是一个全新的维度，换个角度看问题，
将图像转换到频域，高频部分代表图像的细节、纹理信息，
低频部分代表图像的轮廓信息，可以再特定的“频率”范围内对图像进行处理，
就像是用显微镜看图像一样，能挖掘图像更加广阔的信息。

离散余弦变换是一种频率域转为到空间域的数学工具（函数），
它为频率域与空间域架起一座桥梁。

离散余弦变换是**离散傅里叶变换（DFT）**的一种特殊形式，特殊点就在于其原始变换信号是一个实偶函数。

DCT变换较DFT变换具有更好的频域能量聚集度，
那么对于那些不重要的频域区域和系数就能够直接裁剪掉，
因此，DCT变换非常适合于图像压缩算法的处理，
例如现在大名鼎鼎的jpeg就是使用了DCT作为图像压缩算法。

二维DCT变换公式如下：

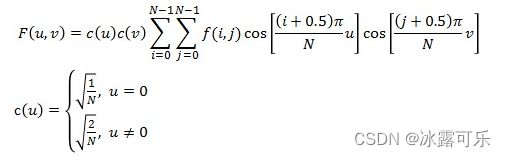
由公式我们可以看出，上面只讨论了二维图像数据为方阵的情况，
在实际应用中，如果不是方阵的数据一般都是补齐之后再做变换的，
重构之后可以去掉补齐的部分，得到原始的图像信息，这个尝试一下，应该比较容易理解

另外，由于DCT变换高度的对称性，
在使用Matlab进行相关的运算时，我们可以使用更简单的矩阵处理方式：

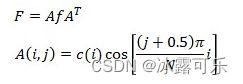
clear;
clc;
% 正变换
X=round(rand(4)*100)   %产生随机矩阵
A=zeros(4);
for i=0:3
    for j=0:3
        if i==0
            a=sqrt(1/4);
         else
             a=sqrt(2/4);
         end            
         A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4);
    end
end

Y=A*X*A'        %DCT变换

%反变换
for i=0:3
    for j=0:3
         if i==0
             a=sqrt(1/4);
         else
             a=sqrt(2/4);
         end            
         A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4); %生成变换矩阵
     end
end

X1=A'*Y*A  %DCT反变换恢复的矩阵

% Matlab版
YY=dct2(X)      %Matlab自带的dct变换
XX=idct2(YY)    %Matlab自带的idct逆变换

%读取图像
X=imread('lena.jpg'); 
X=rgb2gray(X);
%读取图像尺寸
[m,n]=size(X); 
%给图像加噪
Xnoised=imnoise(X,'gaussian',0.01); 
%输出加噪图像
subplot(121); 
imshow(Xnoised);
%DCT变换
Y=dct2(Xnoised); 
I=zeros(m,n);
%高频抑制
I(1:m/3,1:n/3)=1; 
Ydct=Y.*I;
%逆DCT变换
Y=uint8(idct2(Ydct)); 
%结果输出
subplot(122);
imshow(Y);

---

总结

提示：重要经验：

1）噪声有椒盐噪声、高斯噪声等等
2）中值滤波，均值滤波应对椒盐噪声，高斯平滑，双边滤波（双线性变换），应对高斯噪声，还有小波变换，DCT变换滤波
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。