05 线性代数【动手学深度学习v2】

1.背景

我们讲的多维数组是一个计算机的概念，多维数组是一个纯计算机的语言，它和C++的数组一样。但线性代数，同样一个东西，但是它是在数学上的表达，所以它有数学上的意义，我们不需要太多的数学上的知识，我们这里还是稍微的讲一下，我们就简单的入门一下。

• 简单操作
  $$c=a+b;c=a\cdot b;c=\sin a$$
• 长度
  $$|a|=\{\begin{array}{rl}& a,a>0\\ & \\ & -a;a<0\end{array}$$
  $$|a+b|\le |a|+|b|$$
  $$|a\cdot b|=|a|\cdot |b|$$
  
  
  
  
  
  
  
  

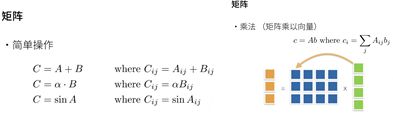
2.线性代数实现

• 标量简单运算

IN [1]: import torch
IN [2]: x = torch.tensor([3.0])
IN [3]: y = torch.tensor([2.0])
IN [4]: x+y,x*y,x/y,x**y
OUT [1]: (tensor([5.]), tensor([6.]), tensor([0.6667]), tensor([8.]))

• 将向量视为标量值组成的列表

IN [1]: import torch
IN [2]: x = torch.arange(4)
IN [3]: x
OUT [1]: tensor([0, 1, 2, 3])

• 通过张量的索引来访问任意元素

IN [1]: import torch
IN [2]: a = torch.arange(4)
IN [3]: a[0],a[1],a[2],a[3]
OUT [1]: (tensor(0), tensor(1), tensor(2), tensor(3))

• 通过指定两个分量 m 和 n 来创建一个形状为 m x n 的矩阵

IN [1]: import torch
IN [2]: x = torch.arange(20).reshape(5,4) # 通过 reshape来生成一个 5行4列的矩阵
IN [3]: x
OUT [1]:tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])
IN [4]:: x.T # x的转置矩阵
OUT [2]: tensor([[ 0,  4,  8, 12, 16],
        [ 1,  5,  9, 13, 17],
        [ 2,  6, 10, 14, 18],
        [ 3,  7, 11, 15, 19]])

• 对称矩阵 A 等于其转置 ($A=A^T$)

IN [1]: import torch
IN [2]: B = torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
IN [3]: B == B.T
OUT [1]:		

• 就像向量是标量的推广，矩阵式向量的推广一样，我们可以构建具有更多轴的数据结构

IN [1]: import torch
IN [2]: B = torch.arange(24).reshape(2,3,4)
OUT [1]:tensor([[ 0,  4,  8, 12, 16],
        [ 1,  5,  9, 13, 17],
        [ 2,  6, 10, 14, 18],
        [ 3,  7, 11, 15, 19]])		

• 给定具有相同形状的任何张良，任何按元素二元运算的结果都将是相同形状的张量

IN [1]: import torch
IN [2]: A = torch.arange(20,dtype=torch.float32).reshape(5,4)
IN [3]: B = A.clone() # 通过分配新内存，将 A 的一个副本分配给 B
IN [4]: A,B,A+B
OUT [1]:(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  2.,  4.,  6.],
         [ 8., 10., 12., 14.],
         [16., 18., 20., 22.],
         [24., 26., 28., 30.],
         [32., 34., 36., 38.]]))		

• 两个矩阵按元素乘法称为 哈达玛积

IN [1]: import torch
IN [2]: A = torch.arange(20,dtype=torch.float32).reshape(5,4)
IN [3]: B = A.clone() # 通过分配新内存，将 A 的一个副本分配给 B
IN [4]: A*B
OUT [1]:(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[  0.,   1.,   4.,   9.],
         [ 16.,  25.,  36.,  49.],
         [ 64.,  81., 100., 121.],
         [144., 169., 196., 225.],
         [256., 289., 324., 361.]]))	

• 计算其元素的和

IN [1]: import torch
IN [2]: x = torch.arange(4,dtype=torch.float32)
IN [3]: x ,x.sum()
OUT [1]:(tensor([0., 1., 2., 3.]), tensor(6.))	

• 求解矩阵的均值

IN [1]: import torch
IN [2]: A = torch.arange(40).reshape(2,5,4)
IN [3]: A.shape,A.sum(),A.mean()
OUT [1]:	
IN [4]:A.mean(axis=0)
OUT [2]:(tensor([[[ 0,  1,  2,  3],
          [ 4,  5,  6,  7],
          [ 8,  9, 10, 11],
          [12, 13, 14, 15],
          [16, 17, 18, 19]],
 
         [[20, 21, 22, 23],
          [24, 25, 26, 27],
          [28, 29, 30, 31],
          [32, 33, 34, 35],
          [36, 37, 38, 39]]]),
 tensor(780))
​

• 计算总和或均值时，保持轴数不变

IN [1]: import torch
IN [2]: A = torch.arange(40).reshape(2,5,4)
IN [3]: sum_A = A.sum(axis=1,keepdim=True)
IN [4]: sum_A,sum_A.shape
OUT [1]:(tensor([[[20, 22, 24, 26],
          [28, 30, 32, 34],
          [36, 38, 40, 42],
          [44, 46, 48, 50],
          [52, 54, 56, 58]]]),
 torch.Size([1, 5, 4]))	

• 某个轴计算 A 元素的累计总和

IN [1]: import torch
IN [2]: A = torch.arange(40).reshape(2,5,4)
IN [3]: cumsum_A = A.cumsum(axis=0)
IN [4]: cumsum_A,cumsum_A.shape
OUT [1]:(tensor([[[ 0,  1,  2,  3],
          [ 4,  5,  6,  7],
          [ 8,  9, 10, 11],
          [12, 13, 14, 15],
          [16, 17, 18, 19]],
 
         [[20, 22, 24, 26],
          [28, 30, 32, 34],
          [36, 38, 40, 42],
          [44, 46, 48, 50],
          [52, 54, 56, 58]]]),
 torch.Size([2, 5, 4]))	

• 点积是相同位置的按元素乘积的和,相同位的元素相乘后求和

IN [1]:import torch
IN [2]:x = torch.arange(4.0)
IN [3]:y = torch.ones(4,dtype=torch.float32)
IN [4]:z = torch.dot(x,y)
IN [5]:x,y,z
OUT [1]:(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))	

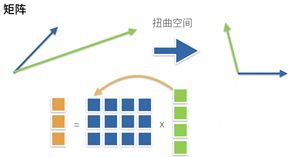
• 矩阵向量 AX 是一个长度为 m 的列向量，其$i^{th}$元素是点积 $a_i^{T}x$ a=5x4,x=4

IN [1]:import torch
IN [2]:x = torch.arange(20,dtype=torch.float32).reshape(5,4)
IN [3]:y = torch.ones(4) 
IN [4]:z = torch.mv(x,y)
IN [5]:x,y,z
OUT [1]:(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([1., 1., 1., 1.]),
 tensor([ 6., 22., 38., 54., 70.]))	

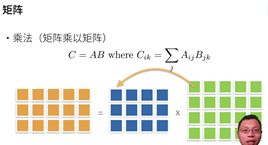
• 矩阵乘法 AB 看作是简单地执行 m 次矩阵-向量积，并将结果拼接在一起形成 N x M 矩阵

IN [1]:import torch
IN [2]:m = torch.arange(20,dtype=torch.float32).reshape(5,4)
IN [3]:n = torch.ones(28,dtype=torch.float32).reshape(4,7)
IN [4]:l = torch.matmul(m,n)
IN [5]:l,l.shape
OUT [1]:(tensor([[ 6.,  6.,  6.,  6.,  6.,  6.,  6.],
         [22., 22., 22., 22., 22., 22., 22.],
         [38., 38., 38., 38., 38., 38., 38.],
         [54., 54., 54., 54., 54., 54., 54.],
         [70., 70., 70., 70., 70., 70., 70.]]),
 torch.Size([5, 7]))	

• $L_2$范数是向量元素平方和的平方根：
  $$||x|{|}_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$

IN [1]: import torch
IN [2]: u = torch.tensor([3.0,-4.0])
IN [3]: torch.norm(u)
OUT [1]:tensor(5.)	

• $L_1$范数是向量元素的绝对值之和：
  $$||x|{|}_1=\sum _{i=1}^N|x_i|$$

IN [1]: import torch
IN [2]: u = torch.tensor([3.0,-4.0])
IN [3]: torch.abs(u).sum()
OUT [1]:tensor(7.)	

• 矩阵的佛罗贝尼乌斯范数是矩阵元素的平方和的平方根：
  $$||x|{|}_F=\sqrt{\sum _{i=1}^m\sum _{i=1}^n{x}_{ij}^2}$$

IN [1]: import torch
IN [2]: torch.norm(torch.ones((4,9)))
OUT [1]:tensor(6.)	

3.按特定轴求和

3.1 矩阵求和-常规

对于一个矩阵为 A = (2,5,4)维来说:

• axis = 0: 求和后的 shape 为 [5,4]
• axis = 1: 求和后的 shape 为 [2,4]
• axis = 2: 求和后的 shape 为 [2,5]
• axis = 1,2: 求和后的 shape 为 [2]

IN [1]:a= torch.ones((2,5,4))
IN [1]:a.shape,a.sum(axis=0).shape,a.sum(axis=1).shape,a.sum(axis=2).shape
OUT [1]:(torch.Size([2, 5, 4]),
 torch.Size([5, 4]),
 torch.Size([2, 4]),
 torch.Size([2, 5])))

3.2 矩阵求和-keepdims

对于一个矩阵为 A = (2,5,4)维来说，要满足 keepdims = True来分析如下：

• axis = 0: 求和后的 shape 为 [1,5,4]
• axis = 1: 求和后的 shape 为 [2,1,4]
• axis = 2: 求和后的 shape 为 [2,5,1]

IN [1]:a= torch.ones((2,5,4))
IN[1]:a.shape,a.sum(axis=0,keepdims=True).shape,a.sum(axis=1,keepdims=True).shape,a.sum(axis=2,keepdims=True).shape
OUT [1]:(torch.Size([2, 5, 4]),
 torch.Size([1, 5, 4]),
 torch.Size([2, 1, 4]),
 torch.Size([2, 5, 1]))

4. QA 问题解答

• 问题1：这么转换有什么负面影响吗？比如数值变得稀疏？
  答：如果我们有一个字符串(100个字符)，我们想把它变成一个数值(变成100列)，而绝大部分情况里面的数值会变成0，所以整个数值就变得十分的稀疏。而稀疏化确实会带来很多问题，比如你有一列(100万行，但每个元素都不一样，就是一个 ID)，如果我们要做稀疏化，那么就会变成100万个列的数据，且每个列中就有一个为1的数，那么这个值就会把数据变得非常的大，非常的占用内存，为了解决上述问题，我们需要用一个稀疏矩阵来存储数据，而对于机器学习来说，稀疏矩阵没什么影响的。
• 问题2：为什么深度学习用张量表示？
  答：整个机器学习都是用张量来计算表示的。这个是一路发展起来的。深度学习是机器学习的一块，机器学习是统计学习的一个计算版本，统计学家觉得机器学习是计算机的人对于统计的理解，统计学家更偏向于数学点，但机器学习其实是同样一个东西，只不过是计算机人用计算机进行的实现。对于统计学家来说，张量是常用的，而这个习惯也一直流传下来。
• 问题3：求 copy 与 clone 的区别(是关于内存吗？)
  答：copy 可能是不copy 内存的，这个分为浅copy和深copy两种，而 clone 是一定复制内存的
• 问题4：对哪一维求和就是消除哪一维可以这么理解吗？
  答：可以这么理解，对于 axis=0维求和就是把这个维度去掉。
• 问题5: torch 不区分行向量和列向量吗？
  答：一维张量其实就是 行向量，而对于 列向量 来说我们一般用矩阵的形式表示[N,1],我们可以用二维的矩阵来区分，比如 行向量为 [1,N],列向量为 [N,1] ;
• 问题6：sum(axis=[0,1])怎么求？
  答：比如我们有 A.shape(2,3,4) ，那么 A.sum(axis=[0,1]).shape 为[4]
• 问题7：稀疏的时候可以把它当成单词做词向量解决吗？
  答：词向量为word2vec也叫word embeddings，后面我们会讲的，它确实可以当作一个稀疏的查表，但不是每一次都是可以当作词向量来解决的，但绝大多数情况下我们是用稀疏来解决这个问题的。我们会在后续的NLP中详解这个问题的。
• 问题8 ： 张量的概念在机器学习和数学有哪些主要的区别吗？
  答：机器学习里面的张量其实不是数学概念中的张量，它大部分情况下都是一个多维的数组，它跟数学的张量是不一样的。而且就算是深度学习，我们对于大部分的运算都是矩阵运算，我们都不太会运用到数学上张量的概念。机器学习中的张量只是我们说的顺口一些而已。
• 问题9： 这门课是不是只讲基于pytorch的神经网络算法？学习其他的框架可以先听这门课吗？
  答：pytorch只是目前比较流行的框架而已，我们可以把它当作一个工具看待，比如说自行车和汽车，这两种工具都能够将我们从地点A运送到地点B，但是我们现在更倾向于汽车，因为它快嘛，就像pytorch一样，它仅仅是一个工具，能够更好的帮你实现神经网络，我们不能把自己局限于工具中，而是要思考工具背后的很多思想，这样随着时代的发展，我们能够更好的迁移到新的工具上。
• 问题10：请问老师 ，病理图片的SVS格式和医生勾画的区域XML格式的文件怎么进行预处理？
  答：有两种做法，第一你可以用像素级别图片来处理，比如用手写问题来解决，第二你可以当作XML当作一个结构化语言来处理，用NLP手段来解决；你可以用任意一个或者两个都用的方式来解决问题。