Counterfactual Attention Learning for Fine-Grained Visual Categorization and Re-identification 论文学习

论文地址：https://arxiv.org/pdf/2108.08728.pdf
Github地址：https://github.com/raoyongming/CAL

Abstract

注意力机制在细粒度视觉分类任务上非常有效。本文介绍了一个反事实的注意力学习方法，基于因果推理来学习更加有效的注意力。现有的方法都基于传统的概率来学习注意力，本文作者提出利用反事实因果关系来学习注意力，为评价注意力的质量提供了一个强力的工具，提供的监督信号可有效地指导训练过程。作者通过反事实介入，分析学到的注意力对网络预测的影响，然后最大化该影响来促使模型去学习更加有用的注意力。在实验环节，作者在各种细粒度识别任务（包括细粒度图像分类、行人重识别、车辆重识别等）上评测了该方法，都有显著的提升。

1. Introduction

注意力是人类视觉感知最基本的机制。当我们面对一个复杂的场景，我们可以选取兴趣区域，利用注意力来缩小搜索区、快速识别。人们尝试将人的注意力机制建模到计算机系统中，通过发现高判别度的区域来实现高效的识别，缓解由背景凌乱、遮挡、姿态变化造成的不良影响。要想区分次要的视觉类别，关键在于找到那些细微的差异，注意力机制就是一个很有效的办法，它已成为诸多SOTA方法的核心。

图1. CUB 注意力可视化。作者分别展示了原图片、基线注意力图、反事实学习的注意力图。从左边可以看到，本文的注意力图能更好地聚焦到目标上。从右边可以看到，本文方法更倾向于观察整个物体，而非物体的局部。

尽管应用广泛，但如何学习有效的注意力鲜被深究。大多数的方法都通过弱监督的方式来学习注意力，注意力模块只受到损失函数监督，缺乏一个强效的监督信号来指导学习过程。概率方法只能显式地监督预测结果（比如分类任务的类别概率），忽略了预测结果和注意力之间的因果关系。那些方法也无法教电脑来区分主要线索（main clues）和片面线索（biased clues）。比如，如果某一类的多数样本都将天空作为背景，那么注意力模型也会将天空当作判别区域。尽管这些片面线索可能对当前数据集的分类有帮助，但注意力模型应该只关注于判别模式（主要线索）。此外，直接从数据当中学习会使得模型聚焦于物体的部分属性，而非全部属性，这会制约模型在测试集上的泛化能力。所以作者认为现有的注意力学习机制不是最优的，它们学到的并不总是有效的，该注意力缺乏判别力、清晰的定义和鲁棒性。如图1所示，训练好的注意力模型中仍然会存在具有误导性的、散乱的注意力，造成预测错误。为了更好地理解该现象，作者分析了 CUB 数据集（图2）的内部属性（由该数据集提供）和外部环境（人工搜集）。可以看到属性和环境是有偏差的，说明背景和单个部分都不算可靠的分类线索。所以我们需要超越传统的最大似然方法，设计新的注意力学习方法来减轻数据偏差的影响。

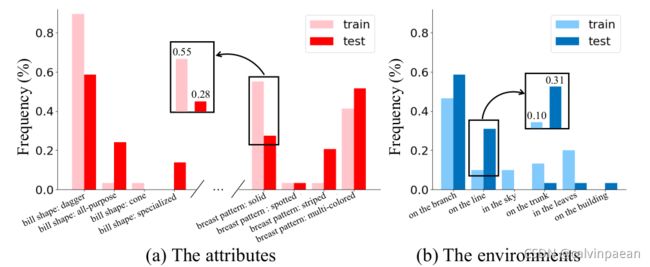
图2. CUB 的内部属性和外部环境的偏差。以环绕翠鸟为例，根据不同属性和环境的统计数据，列出了训练集和测试集之间存在的偏差。

由于缺乏有效的工具来量化评估注意力的质量，纠正错误的注意力很有难度。一个直接的办法就是利用额外的标注信息（如边框或分割mask），显式地得到兴趣区域。但是这些方法需要大量的人工付出，很难大规模扩展。考虑到注意力在细粒度识别任务的重要地位，设计一个无需人工监督即可评价注意力质量的方法就很有必要，从而进一步优化学到的注意力。

本文提出了一个反事实的注意力学习（CAL）方法，基于因果推理来增强注意力学习。作者设计了一个工具来分析学到的注意力的作用，它利用了反事实因果关系。基础思想就是，通过比较事实（fact, 学到的注意力）和反事实（counterfactuals, 无关的注意力）对最终预测结果的影响，量化注意力的质量。然后最大化这种差异，促使网络学习更有效的注意力，降低训练集的片面性影响。

该方法与模型是无关的，可以作为一个即插即用的模块用到各种视觉注意力模型中。该方法的计算效率很高，只在训练时增加了一点计算成本，推理时没有增加计算量。作者在三个细粒度识别任务上进行了方法评测，包括细粒度图像分类（CUB200-2011、Stanford Cars、FGVC Aircraft）、行人重识别（Market1501、DukeMTMC-ReID、MSMT17）和车辆重识别（Veri-776和VehicleID）。作者将该方法添加到了 multi-head 注意力基线模型中，在所有的基准上都优化了基线模型。

2. Related Work

细粒度视觉识别。注意力机制在细粒度视觉识别任务上扮演着无可替代的作用。例如，在细粒度图像分类任务上，Sermanet 等人率先在细粒度识别问题上采用注意力机制，提出了一个 RNN 模型学习注意力。Liu 等人拓展了这个想法，利用增强学习实现注意力。后续研究包括 MA-CNN、MAMC、WS-DAN 等进一步改良了这些方法，通过自下而上的方式设计注意力模型，在细粒度识别基准上取得了优异成绩。注意力模型在行人/车辆重识别任务上也很有效，可解决图像匹配问题，提升CNN特征的判别力。比如，Liu 和 Lan 等人利用注意力模型定位出图像的显著区域，进行行人重识别。Xu 和 Zhao等人设计了肢体检测器，在注意力模型中使用了人体结构。其他一些方法在视频行人重识别任务上采用了注意力机制，探索视频的关键部分。Khorramshahi等人提出了自适应的注意力模型，显著优化了车辆重识别方法。

视觉领域的因果推理。近些年，人们开始探索将深度学习和因果推理结合起来。因果关系分析在多个领域被成功应用，包括可解释机器学习、NLP、增强学习和对抗学习。人们也尝试用因果关系来缓解数据集的偏差问题，如图像分类，场景图生成和视觉常识推理。本文第一次研究了注意力模型中的因果关系，开拓了一个新的方向。

3. 方法

图3. CAL 方法的框架。作者首先将原注意力替换为随机注意力，进行反事实介入。然后，从原分类结果中扣除反事实分类结果，分析学到的注意力的作用，在训练过程中最大化它们。

3.1 细粒度识别的注意力模型

首先作者回顾了细粒度识别任务的注意力模型。给定一张图片$I$和对应的CNN特征图$\mathbf{X}=f(I)$，大小是$H\times W\times C$。视觉空间注意力模型$\mathcal{M}$的目的是找到图像中的判别区域，加入物体的结构信息来改进 CNN 特征图。注意，尽管方法[57]提出给主干网络加装注意力模块，但本文遵循了主流方法，分别学习基本特征图和注意力图。研究表明，这样设计更加灵活、通用，因为它们不涉及到模型本质。

$\mathcal{M}$有多个变体，大致可以分为两类。第一类是学习“硬”注意力图，每个注意力都用一个边框或分割mask表示，覆盖了一定的兴趣区域。这一类方法通常和目标检测、语义分割方法紧密关联。例子包括递归注意力模型[39]和全卷积注意力网络[31]。与硬注意力不同，大量方法使用的是“软”注意力图，更容易优化。本文基线模型采用了 multi-head 注意力模块[65,50,19]。该注意力模型学习物体局部的空间分布，可以表示为$\mathbf{A}\in {\mathbb{R}}_{+}^{H\times W\times M}$，其中$M$是注意力个数。注意力图可计算为

$$\mathbf{A}=\{{\mathbf{A}}_1,{\mathbf{A}}_2,...,{\mathbf{A}}_M\}=\mathcal{M}(\mathbf{X}),\text{\hspace{1em}(1)}$$

其中，${\mathbf{A}}_i\in {\mathbb{R}}_{+}^{H\times W}$是注意力图，覆盖一定区域，比如鸟的翅膀或人的衣服。通过一个2D卷积层和 ReLU 激活函数来实现注意力模型$\mathcal{M}$。然后用注意力图对特征图进行软加权，再通过全局平均池化$\phi$来聚合：

$${\mathbf{h}}_i=\phi (\mathbf{X}\ast {\mathbf{A}}_i)=\frac{1}{HW}\sum _{h=1}^H\sum _{w=1}^W{\mathbf{X}}^{h,w}{\mathbf{A}}_i^{h,w},\text{\hspace{1em}(2)}$$

$\ast$表示两个张量的逐元素相乘。按照[19]的操作，作者将不同部分的表征结合起来，得到全局表征$\mathbf{h}$

$$\mathbf{h}=\text{normalize}([{\mathbf{h}}_1,{\mathbf{h}}_2,...,{\mathbf{h}}_M]),\text{\hspace{1em}(3)}$$

将这些表征concat起来，再做归一化操作。最终的表征$\mathbf{h}$可以输入进图像分类任务的分类器（如全连接层），或者图像提取任务的距离度量算法。整体框架如图3所示。

3.2 Attention Models in Causal Graph

在我们介绍反事实（counterfactual）方法之前，作者首先介绍如何将上述模型表示为因果图（causal graph）。因果图也叫结构因果模型，是一个有向非循环图$\mathcal{G}=\{\mathcal{N},\mathcal{E}\}$。每个变量对应着$\mathcal{N}$的一个节点，因果连接了$\mathcal{E}$表示这些变量彼此间的关系。如图3所示，我们可以用因果图的节点来表示注意力模型的变量，包括 CNN 特征图（或输入图像）$X$、学到的注意力图$A$和最终的预测$Y$。连接了$X\to A$表示将 CNN 特征图作为注意力模型的输入，输出对应的注意力图。$(X,A)\to Y$表示特征图和注意力图一起决定了最终的预测结果。连接$\mathcal{E}$编码了节点间的因果关系，节点$X$就是$A$的因果父，$Y$是$X$和$A$的因果子。注意，因为我们没有给主干网络与注意力模型施加任何的限制，因果图也可代表其它的注意力模型。所以，本方法与模型是无关的，可以拓展到其它的注意力学习问题上去。

3.3 Counterfactual Attention Learning

传统的似然方法只监督最终的预测结果$Y$来优化注意力，它将模型看作为一个黑盒子，而忽略了学到的注意力图是如何影响预测结果的。然而因果推理可以帮我们跳出黑盒子，分析变量间的因果关系。所以作者使用了因果关系来计算学到的注意力的质量，促使网络产生更多重要的注意力图来提升模型。

有了因果图，我们可直接操纵多个变量的值并观察效果，从而分析因果关系。在因果推理领域，该操作叫做intervention，可记做$do(\cdot )$。当我们想深入了解某变量的作用时，可以抹去该变量所有的进入连接，给其赋一个特定值。比如，$do(A=\overline{\mathbf{A}})$表示我们想让$A$的值为$\overline{\mathbf{A}}$，并抹去连接$X\to A$来迫使变量不再受它的因果父$X$的影响。

受到因果推理方法的启发，作者提出了采用counterfactual intervention来研究学到的视觉注意力的影响。通过一个想象出来的 intervention 来调整各变量的状态（假设这些变量的状态都是不同的），从而实现counterfactual intervention。比如，我们进行counterfactual intervention $do(A=\overline{\mathbf{A}})$，可先想象一个不存在的注意力图$\overline{\mathbf{A}}$，替换学到的注意力图，保证特征图$X$不变。根据(2)和(3)，在完成 intervention $A=\overline{\mathbf{A}}$ 后，我们就可得到最终的预测$Y$：

$$Y(do(A=\overline{\mathbf{A}}),X=\mathbf{X})=\mathcal{C}([\phi (\mathbf{X}\ast {\overline{\mathbf{A}}}_1),...,\phi (\mathbf{X}\ast {\overline{\mathbf{A}}}_M)]),\text{\hspace{1em}(4)}$$

其中$\mathcal{C}$是分类器。在实际操作中，我们可以用随机注意力、均匀注意力或反转注意力来作为 counterfactuals。4.4节可以看到这些方法的评测结果。

按照[41,54,53]，学到的注意力对预测结果的影响可以用$Y(A=\mathbf{A},X=\mathbf{X})$和 counterfactual $Y(do(A=\overline{\mathbf{A}}),X=\mathbf{X})$之间的差异表示：

$$Y_{\text{effect}}={\mathbb{E}}_{\overline{\mathbf{A}}\sim \gamma }[Y(A=\mathbf{A},X=\mathbf{X})-Y(do(A=\overline{\mathbf{A}}),X=\mathbf{X})]\text{\hspace{1em}(5)}$$

其中$Y_{\text{effect}}$表示对预测结果的影响，$\gamma$是 counterfactual 注意力的分布。注意力的影响可以用下面的方式解释，与错误的注意力相比，该注意力如何提升最终的预测结果。所以，我们可以用$Y_{\text{effect}}$来评价一个注意力的质量。

此外，我们可将注意力质量当作一个监督信号，指导注意力的学习过程。新的目标函数就是：

$$\mathcal{L}={\mathcal{L}}_{ce}(Y_{\text{effect}},y)+{\mathcal{L}}_{\text{others}}\text{\hspace{1em}(9)}$$

$y$是分类标签，${\mathcal{L}}_{ce}$是交叉熵损失，${\mathcal{L}}_{\text{others}}$表示原来的目标函数，如标准的分类损失。通过优化这个新的目标函数，我们期望：1) 注意力模型应该可以尽可能地提升预测结果，促使注意力发现最具判别力的区域，避免次优结果。2) 根据错误的注意力来惩罚预测结果，迫使分类器根据主要线索来做决定，而非偏见线索，降低训练集中偏见成分的影响。

注意，在实际操作中，计算等式5的期望值是不必要的，训练时我们只需为每个注意力选择一个 counterfactual 注意力，这和随机梯度下降的思想是一致的。所以在训练时，额外的计算开支与 CNN 主干网络相比非常小。而在推理时它没有增加计算量。

4. Experiments

Pls read paper for more details.