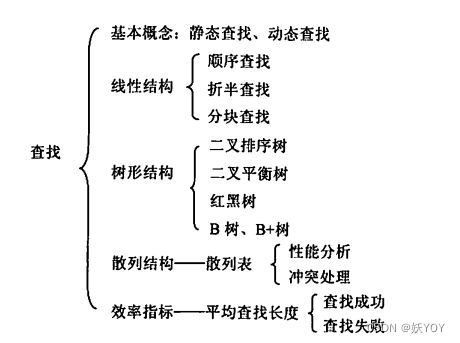
查找算法思想及代码——C语言
数据结构中重要查找算法
- 前言
- 顺序查找法
- 折半查找法
- 分块查找法
- 树形查找法
-
- 二叉排序树,BST
- 平衡二叉排序树,AVL
- 红黑树,RBT
- B树
- B+树
- 散列表(哈希表)
前言
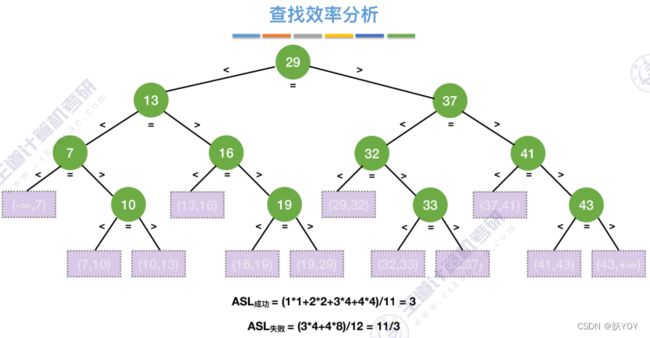
- 查找长度——在查找运算中需要对比关键字的次数称为查找长度
- 平均查找长度(ALS)——所有查找过程中进行关键字的比较次数的平均值,有成功查找和失败下的查找长度
对于哪个步骤不明白的可以在这里看下实际过程
顺序查找法
思想:从头到尾挨个找(反过来也行)
顺序查找时间复杂度: O ( n ) O(n) O(n)
代码:
#define MAXSIZE 100
typedef int ElemType;
typedef struct{ //查找表的数据结构(顺序表)
ElemType *elem; //动态数组基址
int TableLen; //表的长度
}SSTable;
//顺序查找
int Search_Seq(SSTable ST, ElemType key){
int i;
for(i=0; i<ST.TableLen && ST.elem[i] !=key; i++);
//查找成功,则返回元素下标;查找失败,则返回-1
return i==ST.TableLen? -1 : i;
}
//“哨兵”
int Search_Seq_(SSTable ST, ElemType key){
//数据从下标1开始存储
ST.elem[0]=key; //“哨兵”
int i;
for(i=ST.TableLen; ST.elem[i]!=key; i--); //从后往前找
return i; //查找成功,则返回元素下标;查找失败,则返回0
}
折半查找法
又称“二分查找”,仅适用于有序的顺序表
折半查找时间复杂度= O ( log 2 n ) O(\log_2n) O(log2n)
代码:
//结构体
typedef struct{
ElemType *elem;
int length;
}SSTable;
int Search_Bin(SSTable ST,ElemType key){
// 在有序表ST中折半查找其关键字等于key的数据元素。
// 若找到,则函数值为该元素在表中的位置,否则为-1。
int low=0,high=ST.length-1; //置查找区间初值
int mid;
while(low <= high){
mid = (low+high)/2;
if(key==ST.elem[mid])
return mid; //找到待查元素
else if(key<ST.R[mid].key)
high = mid -1; //继续在前半部分查找
else
low = mid + 1; //继续在后半部分查找
}
return -1; //表中不存在待查元素
}// Search_Bin
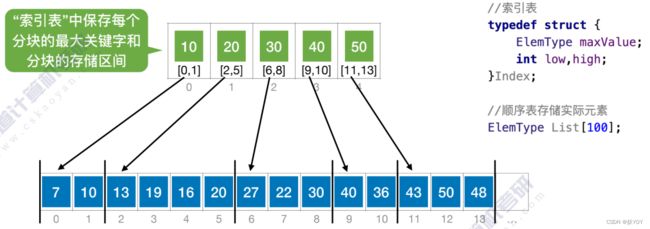
分块查找法
思想:
索引表中记录每个分块的最大关键字、分块的区间;
先查索引表(顺序或折半),再对分块内进行顺序查找。
块内无序,块间有序
设索引查找和块内查找的平均查找长度分别为 L 1 L_1 L1、 L s L_s Ls,则分块查找的平均查找长度为 A S L = L 1 + L s ASL=L_1 + L_s ASL=L1+Ls
A L S = s 2 + 2 s + n 2 s , 当 s = n 时 , A L S 最 小 = n + 1 ALS = \frac{s^2+2s+n}{2s},当s=\sqrt n时,ALS_{最小}=\sqrt{n}+1 ALS=2ss2+2s+n,当s=n时,ALS最小=n+1
树形查找法
n个结点的二叉树最小高度为 ⌊ log 2 n ⌋ + 1 \lfloor{\log_2n}\rfloor + 1 ⌊log2n⌋+1 或是 ⌈ log 2 ( n + 1 ) ⌉ \lceil{\log_2(n+1)}\rceil ⌈log2(n+1)⌉
对具有n个关键字的树型结构,具有n+1个叶结点
二叉排序树,BST
粘一下定义,简单的说就是,左子树节点值 ≤ \leq ≤ 根节点值 ≤ \leq ≤ 右子树结点值

[-] 查找思路:
若树非空,目标值与节点的值比较:
若相等,则查找成功;
若小于根节点,则在左子树上查找,否则在右子树上查找;
查找成功返回节点指针,失败返回NULL
下面是个完整的代码,包括构建二叉树,查找,删除和中序遍历:
#include平衡二叉排序树,AVL
AVL Tree链接
∣ 左 子 树 高 − 右 子 树 高 ∣ ≤ 1 \lvert 左子树高 -右子树高 \rvert \leq 1 ∣左子树高−右子树高∣≤1,平衡因子只可取-1、0或1。
删除,步骤:
①删除节点(方法同,二叉排序树)
- 若删除的节点是叶子,直接删;
- 若删除的节点只有一个子树,用子树顶替删除位置;
- 若删除的节点有两棵子树,用前驱(或后继)结点顶替,并转化未对前驱(或后继)结点的删除。
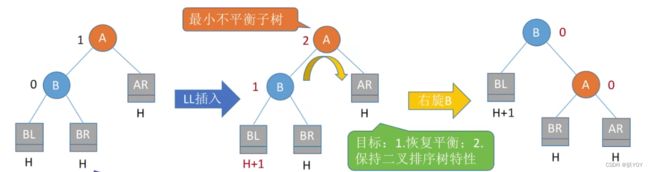
②一路向上找到最小不平衡子树,找不到就over
③找最小不平衡子树下,”个头“最高的儿子,孙子
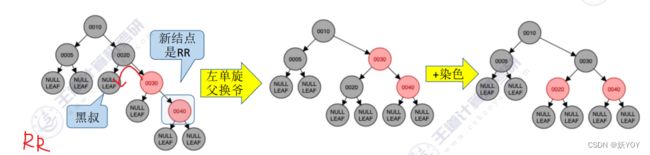
④根据孙子的位置,调整平衡(LL/RR/LR/RL)
- 孙子在LL:儿子右单旋;
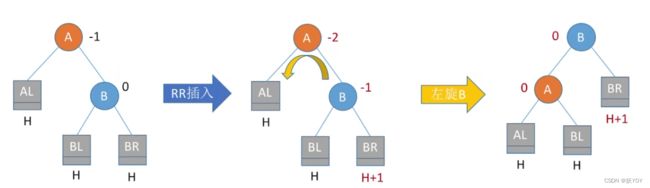
- 孙子在RR:儿子左单旋;
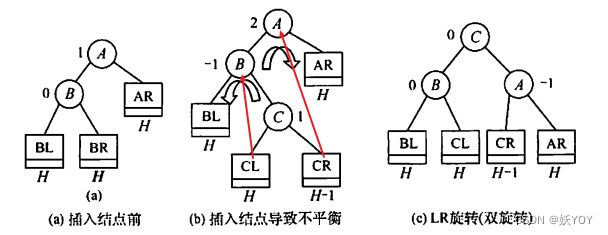
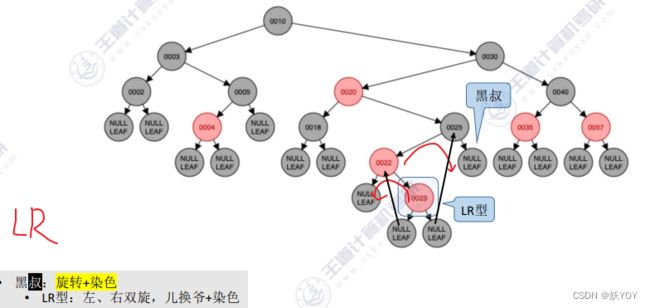
- 孙子在LR:孙子先左旋,再右旋;
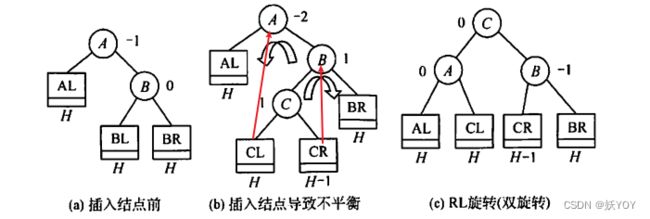
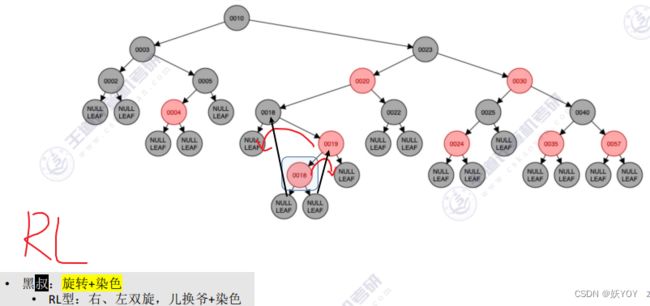
- 孙子再RL:孙子先右旋,再左旋;
⑤如果不平衡向上传导,继续②
红黑树,RBT
Red/Black Tree链接
简要特点:
左右跟,根叶黑
不红红,黑路同
详细特点:
左子树结点值 ≤ \leq ≤ 根结点值 ≤ \leq ≤ 右子树结点值
①每个结点或是红色,或是黑色的;
②根节点是黑色的;
③叶结点(外部结点、NULL结点、失败结点)均是黑色的;
④不存在两个相邻的红结点(即红结点的父节点和孩子结点均是黑色);
⑤对每个结点,从该节点到任一叶结点的简单路径上,所含黑结点的数目相同;
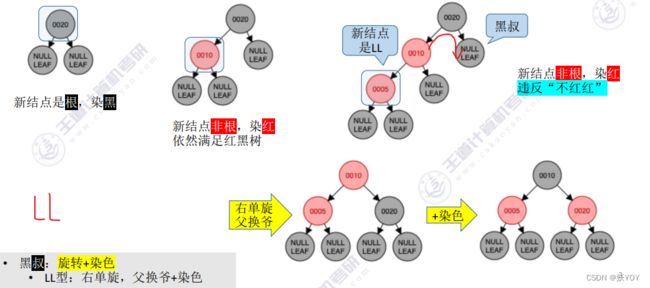
- 黑叔
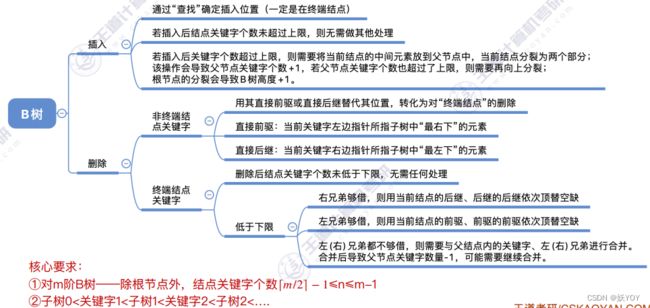
B树
B-Tree 链接
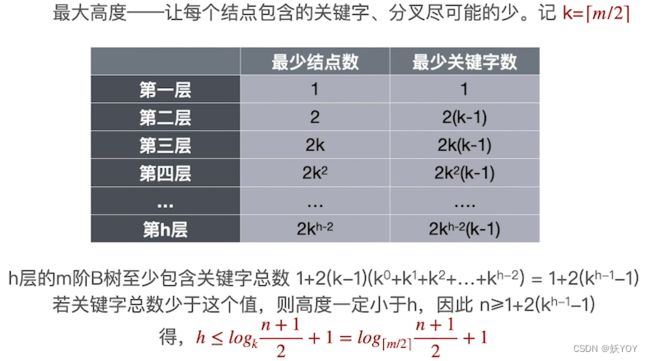
令 k = ⌈ m / 2 ⌉ k=\lceil{m/2}\rceil k=⌈m/2⌉
高 度 为 h 的 m 阶 B 树 , 含 有 关 键 字 个 数 至 少 是 : 2 ⋅ k h − 1 − 1 高度为h的m阶B树,含有关键字个数至少是:2 \cdot k^{h-1}-1 高度为h的m阶B树,含有关键字个数至少是:2⋅kh−1−1
1 + 2 ( k − 1 ) ( k 0 + k 1 + ⋯ + k h − 2 ) = 1 + 2 ( k h − 1 − 1 ) = 2 ⋅ k h − 1 − 1 1+2(k-1)(k^0+k^1+\cdots+k^{h-2}) = 1+2(k^{h-1}-1) = 2 \cdot k^{h-1}-1 1+2(k−1)(k0+k1+⋯+kh−2)=1+2(kh−1−1)=2⋅kh−1−1
高度为h的3阶B树,含有关键字个数至少是: 2 h − 1 2^h-1 2h−1,同完全二叉树(满二叉)
高度为h的5阶B树,含有关键字个数至少是: 2 ⋅ 3 h − 1 − 1 2 \cdot 3^{h-1}-1 2⋅3h−1−1
高度为h的完全二叉树至少 2 h − 1 2^{h-1} 2h−1个结点,最多 2 h − 1 2^{h}-1 2h−1个结点
下面说明下B树特征和形状,先来个5叉树,B树就是在多叉树加一些约束,
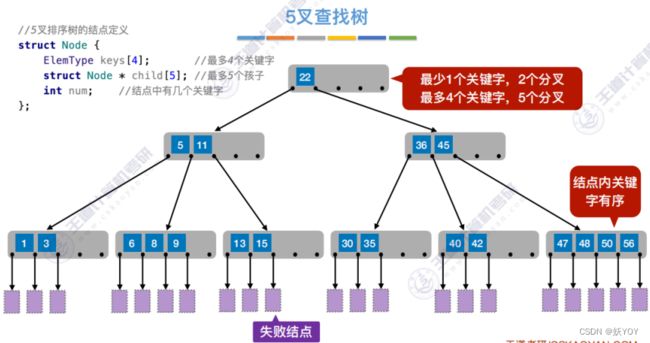
B树结构:
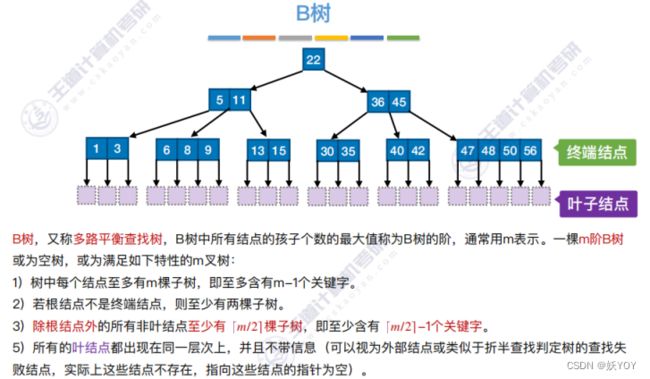
对于高度问题,
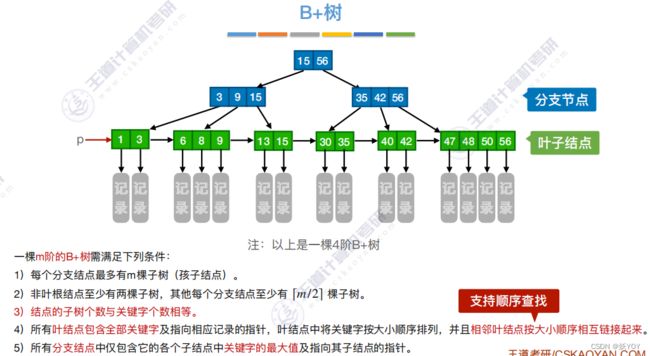
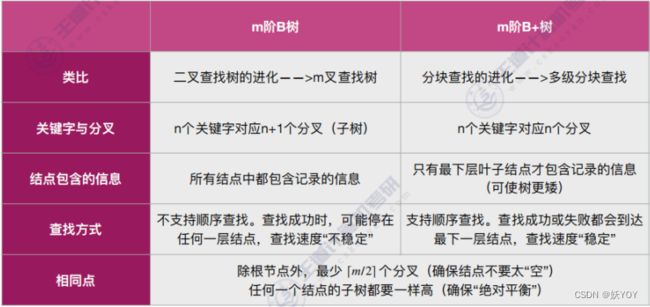
B+树
- B+树有点像是分块查找结构和B树的整合,只在叶子结点存信息,非叶结点仅(上面的)起索引作用,查找也是找到最下层;
- B+树支持顺序查找和随机查找,叶子结点本身依关键字从小到大顺序链接
- 根据B+树的特征,在操作系统中用的挺多,从磁盘里读数据到内存、关系型数据库的“索引”(如MySQL)。
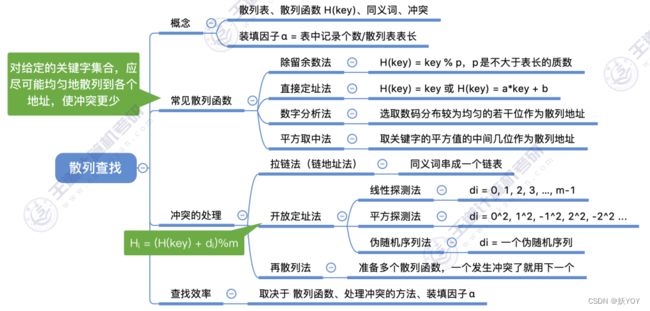
散列表(哈希表)
装填因子 α \alpha α越大,平均查找长度变大,“冲突”越多,查找效率越低
常见的散列函数
- 直接定址法, H ( k e y ) = k e y 或 H ( k e y ) = a × k e y + b H(key) = key 或H(key) = a \times key + b H(key)=key或H(key)=a×key+b
- 除留余数法, H ( k e y ) = k e y % p H(key) = key \% p H(key)=key%p,p取不大于散列表长度m但最接近或等于m的质数
- 数字分析法,设关键字是r进制数(如十进制数) ,而r个数码在各位上出现的频率不一定相同,可能在某些位上分布均匀一些,每种数码出现的机会均等;而在某些位上分布不均匀,只有某几种数码经常出现,此时可选取数码分布较为均匀的若干位作为散列地址。这种方法适合于已知的关键字集合,若更换了关键字,则需要重新构造新的散列函数。例:手机号后四位
- 平方取中法,这种方法得到的散列地址与关键字的每位都有关系,得到的散列地址分布比较均匀,适用于关键字的每位取值都不够均匀或均小于三别地址所需的位数
处理冲突方法
- 拉链法,下图:
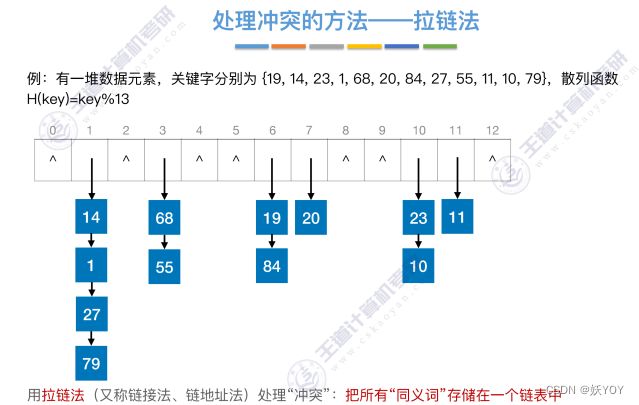
- 开放定址法,下图:

-
①线性探测法: d i = 0 , 1 , 2 , 3 , ⋯ , m − 1 d_i=0,1,2,3,\cdots,m-1 di=0,1,2,3,⋯,m−1,即发生冲突时,每次往后探测相邻的下一个单元是否为空。线性探测法很容易造成同义词、非同义词的“聚集(堆积)”现象,严重影响查找效率产生原因——冲突后再探测一定是放在某个连续的位置。
查找效率分析:
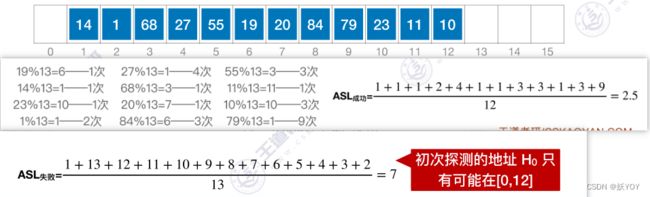
-
②平方探测法,当 d i = 0 2 , 1 2 , − 1 2 , 2 2 , − 2 2 , ⋯ , k 2 , − k 2 d_i=0^2, 1^2, -1^2, 2^2, -2^2, \cdots , k^2, -k^2 di=02,12,−12,22,−22,⋯,k2,−k2时,称为平方探测法,又称二次探测法,其中 k ≤ m / 2 k \leq m/2 k≤m/2。比起线性探测法更不容易产生“聚集(堆积)”问题。
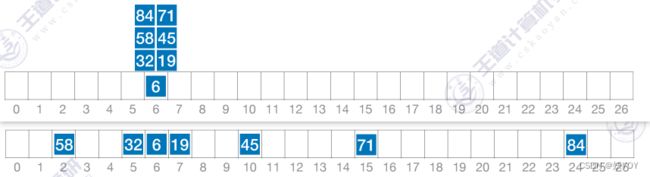
-
③伪随机序列法, d i d_i di是一个伪随机序列,自己定义的,如 d i = 0 , 3 , 5 , 11 , … di= 0, 3, 5, 11, \ldots di=0,3,5,11,…
-
④再散列法(再哈希法):除了原始的散列函数 H ( k e y ) H(key) H(key)之外,多准备几个散列函数,当散列函数冲突时,用下一个散列函数计算一个新地址,直到不冲突为止。
-