【自动驾驶轨迹规划之dubins曲线与reeds-shepp曲线】
目录
1 dubins曲线的简介
2 dubins 曲线的实现与计算
2.1 找到圆心
2.2 找到切点
2.3 画出dubins曲线并计算路径长度
2.4 车辆外形建模
2.5 车辆沿dubins曲线进行运动
2.6 生成车位
3 最短路径的选择
4 reeds-shepp曲线
4.1 reeds-shepp曲线与dubins曲线的区别
4.2 reeds-shepp的分类
4.3 实际的应用
1 dubins曲线的简介
dubins曲线是在满足曲率约束和规定的始端和末端的切线方向的条件下,连接两点的最短路径。在不考虑车辆倒退的情况下,车辆的运动可以分为三类,直线运动(S)、左转(L)、右转(R)。论文中表明任意两点之间的最短距离总可以表示成上述的三种基本运动的组合,并且左转右转的半径都是取最大曲率的时候(即最小半径)。我们令三种基本运动的组合为一个 word ,由于连续两次做同一种基本运动和做一次基本运动是等效的,所以 word经过排列组合后的种类有12个,论文又证明最短路径只在12种中的6种word中去选取。分别是
注意:
(1)有人可能觉得两点最短不就是直线吗,为什么要加入圆弧,因为起点终点是带着航向角的要求的
(2)最短路径在去最小半径的时候取到这是在无障碍的情况下
(3)三种运动都是圆弧时,若不能保证中间的圆弧也取最小半径的话,其他四种情况肯定更好,判断方法就是,起点终点距离是否大于最小半径的6倍
(4)之前的几篇文章分析了很多轨迹规划的算法,但都没有考虑车辆运动学模型,将考虑了运动学模型的dubins曲线与前面的全局路径规划相结合就可以得到真正的轨迹规划
![]()
2 dubins 曲线的实现与计算
2.1 找到圆心
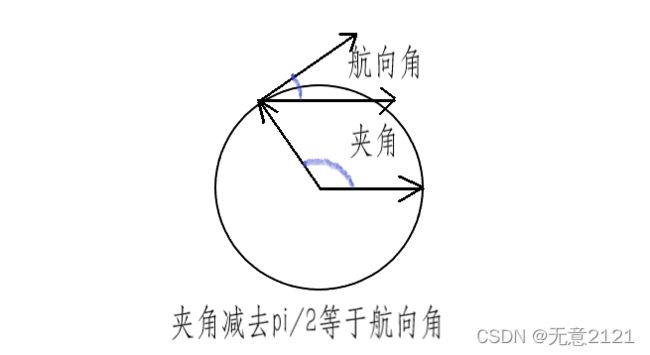
我们定义车辆的航向角a为车头朝向与x轴正方向的夹角,范围是0~2pi。我们在画圆弧的时候需要确定车到圆心的连线与x轴正方向的夹角b才能知道圆心在哪,但是我们只知道车辆的航向角a而暂时不知道夹角b,因此我们的任务是找到这个夹角b与航向角a之间的关系。
首先我们考虑在顺时针旋转的时候(也就是车辆右转R的时候)
已知车辆后轴起点中心坐标(x1,y1)与航向角a与转弯半径r,计算第一个圆弧圆心坐标(x3,y3)
其次我们考虑在逆时针旋转的时候(也就是车辆左转L的时候)
已知车辆后轴中心起点坐标(x1,y1)与航向角a与转弯半径r,计算第二个圆弧圆心圆心坐标(x3,y3)
针对于终点,上述公式也是同理的。
2.2 找到切点
本文以RSR为例,其他的情况同理,就不做推导
这种情况下从圆弧运动转向直线运动的时刻,航向角a未知,但是圆心连线与x轴夹角c可以通过两个圆心坐标来确定,同时航向角a又等于圆心连线与x轴夹角c,所以航向角a可以得到,通过 2.1的推导,我们又可以通过航向角a推算出夹角b,由于圆心(x3,y3)在2.1中推出,所以第一个圆弧切点的坐标(x5,y5)可以由第一个圆弧的圆心(x3,y3)与夹角b确定。第二个圆弧切点的坐标(x6,y6)可以由第二个圆弧的圆心(x4,y4)与夹角b确定。
2.3 画出dubins曲线并计算路径长度
clc
clear all
set(0,'defaultfigurecolor','w');
A=[-1,3,45];B=[6,2,300];r=2;%测试样例
%矩阵里的元素代表起点坐标与航向角
%确定两个圆心的坐标
x3=A(1)+r*sin(deg2rad(A(3)));
y3=A(2)-r*cos(deg2rad(A(3)));
x4=B(1)+r*sin(deg2rad(B(3)));
y4=B(2)-r*cos(deg2rad(B(3)));
a=atan((y4-y3)/(x4-x3));
%确定切点坐标
x5=x3-r*sin(a);
y5=y3+r*cos(a);
x6=x4-r*sin(a);
y6=y4+r*cos(a);
plot([x5,x6],[y5,y6],'b-');hold on;%画出直线
%画出第一个圆弧
i=(deg2rad(A(3))+pi/2):-0.01:(pi/2+a);%代表顺时针的角度变化
x=x3+r*cos(i);
y=y3+r*sin(i);
plot(x,y,'b-');
axis equal;hold on;
%画出第二个圆弧
i=(pi/2+a):-0.01:(deg2rad(B(3))-3*pi/2);%严格来讲这里需要写一个if
x=x4+r*cos(i);
y=y4+r*sin(i);
plot(x,y,'b-');
axis equal;hold on;
%计算路径长度,通过计算圆弧弧度来计算圆弧长度
L=r*((deg2rad(A(3))+pi/2)-(pi/2+a))+sqrt((y4-y3)^2+(x4-x3)^2)+r*((pi/2+a)-(deg2rad(B(3))-3*pi/2));2.4 车辆外形建模
这里可以参考【自动驾驶轨迹规划之最优控制】_无意2121的博客-CSDN博客
function f=carmodel(x,y,a)
%(x,y)为车辆后轴中心,a为车辆航向角
%x=1;y=1;a=0;%测试样例
Lw=0.8;Lf=0.2;Lr=0.2;Lb=0.5;%Lw为前后轴距,Lf为车辆前悬距离,Lr为车辆后悬距离,Lb为车宽。
%画出后轴中心点
plot(x,y,'r.');hold on;
%根据四个顶点画出矩形
plot([x+(Lw+Lf)*cos(a)-0.5*Lb*sin(a),x+(Lw+Lf)*cos(a)+0.5*Lb*sin(a)],[y+(Lw+Lf)*sin(a)+0.5*Lb*cos(a),y+(Lw+Lf)*sin(a)-0.5*Lb*cos(a)],'r-');hold on;
plot([x-Lr*cos(a)-0.5*Lb*sin(a),x+(Lw+Lf)*cos(a)-0.5*Lb*sin(a)],[y-Lr*sin(a)+0.5*Lb*cos(a),y+(Lw+Lf)*sin(a)+0.5*Lb*cos(a)],'r-');hold on;
plot([x-Lr*cos(a)-0.5*Lb*sin(a),x-Lr*cos(a)+0.5*Lb*sin(a)],[y-Lr*sin(a)+0.5*Lb*cos(a),y-Lr*sin(a)-0.5*Lb*cos(a)],'r-');hold on;
plot([x-Lr*cos(a)+0.5*Lb*sin(a),x+(Lw+Lf)*cos(a)+0.5*Lb*sin(a)],[y-Lr*sin(a)-0.5*Lb*cos(a),y+(Lw+Lf)*sin(a)-0.5*Lb*cos(a)],'r-');hold on;2.5 车辆沿dubins曲线进行运动
仍旧以RSR为例,给定车辆的起点坐标与航向角,车辆的终点坐标与航向角,以及最小转弯半径,我们可以知道车辆如何以dubins曲线进行运动。下面是matlab代码
clc
clear all
set(0,'defaultfigurecolor','w');
A=[-1,3,45];B=[6,2,300];r=2;%测试样例
%矩阵里的元素代表起点坐标与航向角
%确定两个圆心的坐标
x3=A(1)+r*sin(deg2rad(A(3)));
y3=A(2)-r*cos(deg2rad(A(3)));
x4=B(1)+r*sin(deg2rad(B(3)));
y4=B(2)-r*cos(deg2rad(B(3)));
a=atan((y4-y3)/(x4-x3));
%确定切点坐标
x5=x3-r*sin(a);
y5=y3+r*cos(a);
x6=x4-r*sin(a);
y6=y4+r*cos(a);
%画出第一个圆弧
Fx=x3+r*cos(deg2rad(A(3))+pi/2);Fy=y3+r*sin(deg2rad(A(3))+pi/2);
for i=(deg2rad(A(3))+pi/2):-0.1:(pi/2+a)%代表顺时针的角度变化
x=x3+r*cos(i);
y=y3+r*sin(i);
plot([x,Fx],[y,Fy],'b-');
axis equal;xlim([-3,8]);ylim([-2,6]);hold on;pause(0.01);
Fx=x;Fy=y;
carmodel(x,y,i-pi/2);
end
Fx=x5;Fy=y5;
for i=x5:0.2:x6
plot([i,Fx],[(y6-y5)/(x6-x5)*(i-x5)+y5,Fy],'b-');
axis equal;xlim([-3,8]);ylim([-2,6]);hold on;pause(0.01);
Fx=i;Fy=(y6-y5)/(x6-x5)*(i-x5)+y5;
carmodel(Fx,Fy,a);
end
%画出第二个圆弧
Fx=x4+r*cos(pi/2+a);Fy=y4+r*sin(pi/2+a);
for i=(pi/2+a):-0.1:(deg2rad(B(3))-3*pi/2);%严格来讲这里需要写一个if
x=x4+r*cos(i);
y=y4+r*sin(i);
plot([x,Fx],[y,Fy],'b-');
axis equal;hold on;
xlim([-3,8]);ylim([-2,6]);hold on;pause(0.01);
Fx=x;Fy=y;
carmodel(x,y,i-pi/2);
end
%计算路径长度
L=r*((deg2rad(A(3))+pi/2)-(pi/2+a))+sqrt((y4-y3)^2+(x4-x3)^2)+r*((pi/2+a)-(deg2rad(B(3))-3*pi/2));2.6 生成车位
将选定两个车位,我们的任务是从一个车位运动到另一个车位,这里车位的外形建模只需把车辆外形加宽加长画图即可。
function f=chewei(x,y,a)
%(x,y)为车辆后轴中心,a为车辆航向角
%x=1;y=1;a=0;%测试样例
Lw=0.8;Lf=0.2;Lr=0.2;Lb=0.5;%Lw为前后轴距,Lf为车辆前悬距离,Lr为车辆后悬距离,Lb为车宽
%需要对其加宽加长
Lf=Lf+0.1;Lr=Lr+0.1;Lb=Lb+0.1;
plot([x+(Lw+Lf)*cos(a)-0.5*Lb*sin(a),x+(Lw+Lf)*cos(a)+0.5*Lb*sin(a)],[y+(Lw+Lf)*sin(a)+0.5*Lb*cos(a),y+(Lw+Lf)*sin(a)-0.5*Lb*cos(a)],'g-');hold on;
plot([x-Lr*cos(a)-0.5*Lb*sin(a),x+(Lw+Lf)*cos(a)-0.5*Lb*sin(a)],[y-Lr*sin(a)+0.5*Lb*cos(a),y+(Lw+Lf)*sin(a)+0.5*Lb*cos(a)],'g-');hold on;
plot([x-Lr*cos(a)-0.5*Lb*sin(a),x-Lr*cos(a)+0.5*Lb*sin(a)],[y-Lr*sin(a)+0.5*Lb*cos(a),y-Lr*sin(a)-0.5*Lb*cos(a)],'g-');hold on;
plot([x-Lr*cos(a)+0.5*Lb*sin(a),x+(Lw+Lf)*cos(a)+0.5*Lb*sin(a)],[y-Lr*sin(a)-0.5*Lb*cos(a),y+(Lw+Lf)*sin(a)-0.5*Lb*cos(a)],'g-');hold on;3 最短路径的选择
前面都是以RSR的情况为例,这样规划出来的路径只能算是在RSR的情况下的最短路径,而不是dubins曲线的最短路径,因此我们需要计算出上述六种组合的路径消耗,从而选出最短路径。更多详细关于dubins曲线路径的计算的介绍可以参考杜宾斯集合的分类 - 科学指导 (sciencedirect.com)
4 reeds-shepp曲线
4.1 reeds-shepp曲线与dubins曲线的区别
上述dubins曲线是针对于车辆不倒退的情况,但是一旦车辆能够倒退,车辆的运动轨迹将更加丰富而复杂,所以reeds-shepp曲线的应用远远多于dubins曲线。原始论文请参考https://faculty.wharton.upenn.edu/wp-content/uploads/2012/04/Car-that-goes-forwards-and-backwards.pdf
![]()
4.2 reeds-shepp的分类
C代表圆弧运动,S代表直线运动,| 代表即将反向运动,u代表两次圆弧运动转过的角相等。大致可分为下面几类
最后所有的word组合达到48种,直线运动(S)、左转(L)、右转(R),+代表前进,-代表后退
4.3 实际的应用
Reeds-Shepp曲线和Dubins曲线特指没有障碍物时的最短路径。如果存在障碍物,那么这样的曲线不再是传统意义上的RS和Dubins曲线了。但实际生活中处处都是障碍物,停车有边界限制,换道时旁边都是车辆,所以我们采取搜索的方式找到最优的reeds-shepp曲线的组合。如下图
![]()
以后的文章中会讲解hybridA*算法(用到启发函数的全局路径规划与考虑局部路径规划的结合),也会讲解RRT*算法(基于采样的搜索与考虑局部路径规划的结合)。