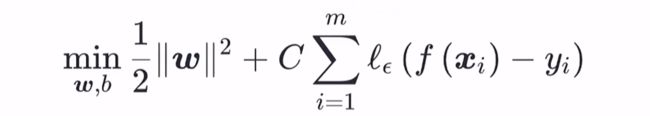西瓜书第六章——支持向量机

---

前言

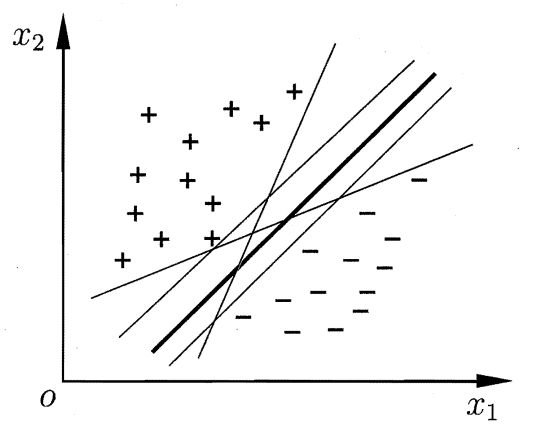
假设这里有一个包含两类的样本数据集 D（该数据集是线性可分的），那么这种简单的二分类问题，我们最基本的的思想就是找一个超平面将数据集划分好，即如上图所示；但是会有多个可行的超平面，我们应该选哪一个呢？这就是支持向量机所考虑的问题：使得学习出的模型既不偏向正样本，也不偏向负样本，泛化能力更好。

---

一、间隔与支持向量

1.1、算法原理

从几何角度，对于线性可分数据集，支持向量机就是找距离正负样本都最远的超平面。相比于感知机，其解是唯一的，且不偏不倚（既不偏向正样本，也不偏向负样本），泛化性能更好。

n维空间的超平面(wTa ＋b =0，其中w, a ∈ 罗:—2
·_超平面方程不唯一
·法向量w和位移项b确定一个唯一超平面
。法向量w垂直于超平面（缩放w , b时，若缩放倍数为负数会改变法向量方向)。法向量w指向的那一半空间为正空间，另一半为负空间
·任意点a到超平面的距离公式为

1.2、超平面

样本空间中的划分超平面可以用线性方程 ωT * x + b = 0 来描述（），其中 ω =（ω1；ω2；ω3…；ωd）为该超平面的法向量，决定了超平面的方向；b为位移项，决定了超平面与原点之间的距离。显然，划分超平面可被法向量 ω 和位移 b 确定。关于超平面的一些性质：

• 超平面方程不唯一；

• 法向量 ω 和位移项 b 确定一个唯一的超平面；

• 法向量 ω 垂直于超平面（缩放 ω、 b 时，若缩放倍数为负数会改变法向量方向)。

• 法向量 ω 指向的那一半空间为正空间，另一半为负空间；

• 任意点 x 到超平面的距离公式为：
  
  任意一点 x0 到超平面 ωT * x + b = 0 的距离公式证明：

  设 x1 为 x0 在超平面上的投影点，因为 x1 在超平面上，所以满足公式 ωT * x1 + b = 0。因此根据向量内积公式可得：

又有以下推导：

所以可以证明出距离公式：

1.3、几何间隔

对于给定的数据集 X 和超平面 ωT * x + b = 0，定义数据集中任意一个样本点（xi，yi），yi ∈ {-1，1}，i = 1，2，3…，m。该点到超平面的几何间隔为：

很容易可以看出，当样本被正确分类时，几何间隔就是到超平面的距离（上述公式的分子负负得正、正正得正）；样本被错误分类时，几何间隔小于 0。
又定义：数据集 X 到超平面 ωT * x + b = 0 的几何间隔为 数据集 X 中所有样本点的几何间隔最小值：

1.4、支持向量机

1.4.1、模型

基于前面所讲的算法思想，支持向量机模型是：在给定线性可分的数据集 X 上，求得 数据集 X 到超平面几何间隔 γ 最大的那个超平面，然后套上一个 sign函数实现分类功能，模型如下：

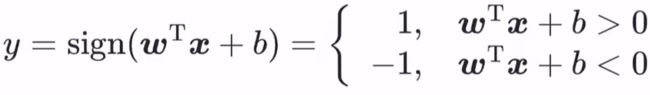
其本质还是跟感知机一样，求超平面。只不过支持向量机是要求泛化能力更好的超平面，数学形式上就是求几何间隔 γ 最大的超平面。

问题：为什么几何间隔 γ 最大的超平面可以保证”离正类样本的也远，离负类样本的也远“？

• 当某个超平面没能正确划分正负样本时，此时 γ < 0，因为要选 γ 最大的，所以肯定不会选此超平面；
• 当某个超平面可以正确划分正负样本时，此时 γ >= 0，此时 几何间隔就等于点到超平面的距离（最小值），所以 γ 最大时，离这些点也达到最远了。

1.4.2、策略

我们的目标已经明确，即找到 max（ γ ），因为 γ 是所有样本点到超平面最小的几何间隔，所以假设 X 中几何间隔最小的样本为（x min，y min），那么支持向量机找超平面的过程可转化为带约束条件的优化问题：

化简上式：

但是该策略可能得到多个最优解，假设（ ω*，b* ）是一个最优解，那么同时扩大 α 倍，（ αω*，αb* ）也是最优解，因为 α 在上式中可完全给消掉，消掉之后也就是第一个最优解的情况了，所以这里 α 完全是没有用的，得到的超平面也与前一个相同。出现它的原因就是没有限制（ ω，b ）这两个参数，所以我们这里设置一个限制，只为得到唯一的最优解（ ω*，b* ）。

其实这里已经得到了最优的超平面，只是没有得到唯一的 ω*，b* ；因为前面讲到，超平面的方程不唯一，就是这个原因，我们才要加一个限制条件，以得到唯一的 ω*，b* 。

我们这里的限制条件为：

对于此方程，因为（x min，y min）是确定的，所以我们得到的（ ω，b ）是唯一的， α 也是唯一的了。最后得到的策略为：
此优化问题为含不等式约束的优化问题，且为凸优化问题，因此可以直接用很多专门求解凸优化问题的方法求解该问题，在这里，支持向量机通常采用拉格朗日对偶来求解，具体原因待求解完后解释，下面先给出拉格朗日对偶相关知识。

二、对偶问题

2.1、凸优化问题

对于—般地约束优化问题：

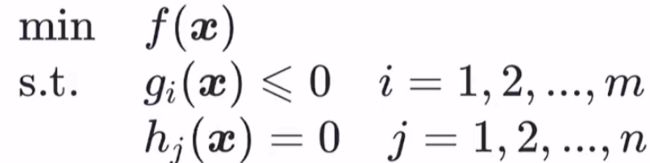
若目标函数 f(x) 是凸函数，约束集合是凸集，则称上述优化问题为凸优化问题。特别地，gi(x) 是凸函数，hj(x) 是线性函数时，约束集合为凸集，该优化问题为凸优化问题。

显然，支持向量机的目标函数 1/2 * ||ω||^2 是关于ω的凸函数，不等式约束 1 - yi (ω T * a + b) 也是关于 ω 的凸函数，因此支持向量机是一个凸优化问题。

2.2、拉格朗日对偶问题

对于—般地约束优化问题（如 2.1 图中所示的问题，不一定是凸优化问题）：

设该问题的定义域和可行集分别为：

显然 可行集 D~ 是定义域 D 的子集。设最优解为 p* = min{ f(x~) }。由拉格朗日定义可得上述问题的拉格朗日函数为：

有了此拉格朗日函数，我们再定义 拉格朗日对偶函数 τ（μ，λ）（此函数没有包含 x 自变量）为 L（x，μ，λ）关于 x 的下界，表示为以下公式：

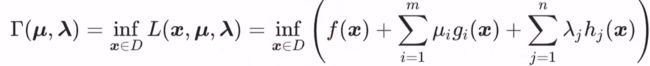
拉格朗日对偶函数的几个重要性质：

1. 性质1：无论上述优化问题是否是凸优化问题，其对偶函数 τ（μ，λ）恒为凹函数；
2. 性质2：当 μ ≥ 0 时， τ（μ，λ）构成了上述优化问题最优值 p* 的下界，即 τ（μ，λ）<= p*

性质2 的证明：假设 x~ ∈ D~是优化问题的可行点，那么该点满足一般约束优化问题中的约束条件：
gi（ x~ ）<= 0，hj（ x~ ）= 0 这两个约束。如果当 μ ≥ 0 ，则有：

根据上述不等式，可以继续推导得到：

所以当 μ ≥ 0 时， τ（μ，λ）<= p* 恒成立，证毕。

我们定义：在满足μ ≥ 0 这个约束条件下求对偶函数最大值的优化问题为拉格朗日对偶问题。（原优化问题，即支持向量机问题（凸函数问题），我们称为主问题）。

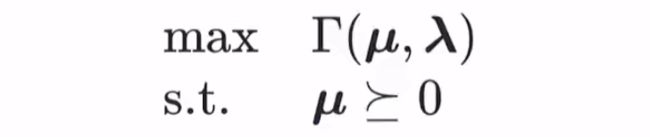
设该优化问题的最优值为 d*，显然 d* ≤ p*，此时称为“弱对偶性"成立，若 d* = p*，则称为“强对偶性"成立。这样终于算是找到了求 p* 的方法。

3. 要使“强对偶性"成立，需要看主问题是否满足某些充分条件。常见的充分条件是Slater条件：主问题是凸优化问题，且可行集 D~ 中存在一点能使得所有不等式约束的不等号成立，则强对偶性成立。显然，支持向量机满足Slater条件。
4. 无论主问题是否为凸优化问题，对偶问题恒为凸优化问题，因为对偶函数 τ（μ，λ）恒为凹函数（加个负号即可转为凸函数)，约束条件 μ ≥ 0 恒为凸集。
5. 设f(x)，gi(x)，hj(x)—阶偏导连续，x*，（μ，λ）分别为主问题和对偶问题的最优解，若强对偶性成立，则x*，（μ，λ）一定满足如下5个条件（称为KKT条件）：
   

2.3、拉格朗日对偶代入主问题

上式将ω，b 合并，得到 ω^，则 L（ω，b，α）是关于 ω^ 的凸函数（海塞矩阵正定性判定的方法），所以 L 函数的最小值就可以通过对 ω^ 求一阶导数，让其为 0 ，即可得到最小值，此最小值即为相应的拉格朗日对偶函数（因为它是下界函数嘛）。

另一种得出拉格朗日对偶函数的方法：

L（ω，b，α）是关于 ω 的凸函数，关于 b 的线性函数。所以当 b 的系数不为 0 时，下确界为 -∞；当 b 的系数为 0 时，下确界就由其他部分来确定，所以 L（ω，b，α） 的下确界（对偶函数）为：

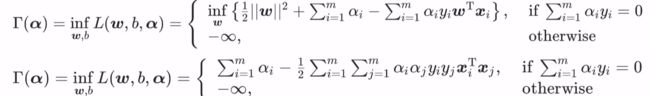
对偶函数找到，那么我们可以将主问题转化为对偶问题了，对偶问题如下：

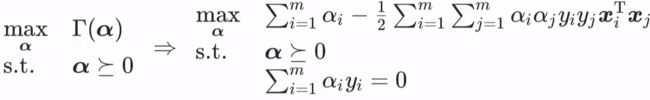
再由强对偶性成立的条件——KKT条件，需要满足以下式子：

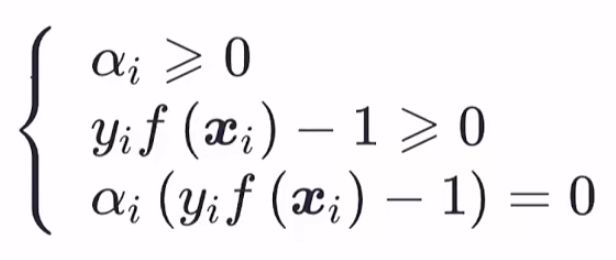
为什么支持向量机通常都采用拉格朗日对偶求解呢?

• 无论主问题是何种优化问题，对偶问题恒为凸优化问题，因此更容易求解（尽管支持向量机的主问题本就是凸优化问题），而且原始问题的时间复杂度和特征维数呈正比（因为未知量是 ω），而对偶问题和数据量成正比（因为未知量是α)，当特征维数远高于数据量的时候拉格朗日对偶更高效
• 对偶问题能很自然地引入核函数，进而推广到非线性分类问题（最主要的原因）

三、软间隔与支持向量回归

前面所讲的支持向量机划分一个泛化能力更好的超平面，它前提是：使用的数据集 X 为线性可分的。然而现实任务中，线性不可分的数据集才是常见的，因此需要允许支持向量机犯错（否则不会找到超平面了）。

3.1、软间隔

从数学角度来说，软间隔就是允许部分样本（但要尽可能少）不满足下式中的约束条件：

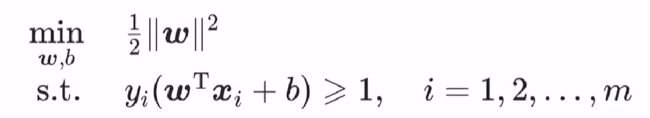
即上述的约束条件可以接受一定灵活性的损失，合格的损失函数要求如下：

• 当满足约束条件时，损失为 0
• 当不满足约束条件时，损失不为 0
• 当不满足约束条件时，损失与其违反约束条件的程度成正比（可选）

只有满足以上要求，才能保证在最小化 （min）损失的过程中，保证不满足约束条件的样本尽可能的少。

我们使用软件隔得到的新的策略为：


C > 0 是一个常数，用来调节损失的权重，显然当 C →＋∞ 时，会迫使所有样本的损失为 0，进而退化为严格执行的约束条件，退化为硬间隔。因此，本式子可以看作支持向量机的一般化形式（既包含硬间隔，也包含软间隔）。

由于 0/1 损失函数非凸、非连续，数学性质不好，使得上式不易求解，因此常用一些数学性质较好的替代损失函数来代替 0/1 损失函数，软间隔支持向量机通常采用的是 hinge （合页）损失来代替 0/1 损失函数：

替换之后，就变为：

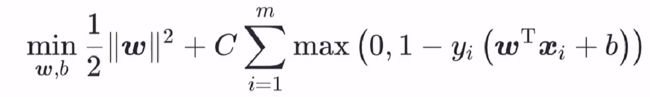
上式中，我们引入一个松弛变量 ξ i ，上述优化问题即等价为：

证明如下：

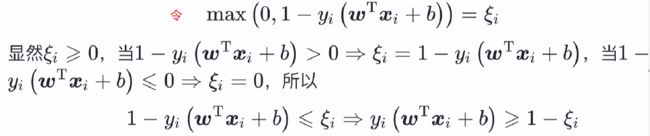
3.2、支持向量回归

相比于线性回归用一条线来拟合训练样本，支持向量回归（SVR）是采用一个以f （x） = ω T * x ＋ b 为中心，宽度为 2ε 的间隔带来拟合训练样本。

落在带子上的样本不计算损失（类比线性回归在线上的点预测误差为0），不在带子上的则以偏离带子的距离作为损失（类比线性回归的均方误差），然后以最小化损失的方式迫使间隔带从样本最密集的地方（中心地带）穿过，进而达到拟合训练样本的目的。

那么SVR的优化问题可以写成如下形式：

1/2 * ||ω||^2 为 L2 正则项，此处引入正则项除了起正则化本身的作用外，也是为了和（软间隔）支持向量机的优化目标保持形式上的一致(在这里不用均方误差也是此目的)，这样就可以导出对偶问题引入核函数，C 为调节损失权重的常数。

同软间隔支持向量机，引入松弛变量 ξ i，令


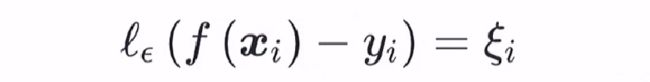
那么 SVR支持向量机的优化问题可以改写为：

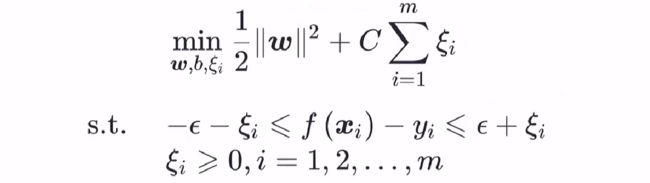
如果两边考虑不同的松弛程度，则有：

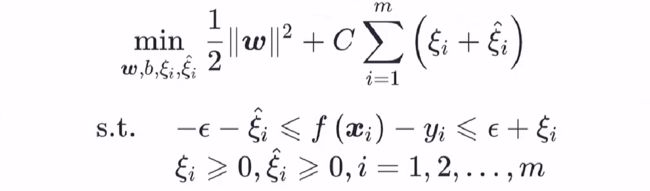
总结

本章讲解基于线性可分数据集上的支持向量机模型，以求得唯一的一个泛化能力更好的超平面，中间介绍超平面、几何间隔等基础概念；然后在分析支持向量机如何求解时，我们又引入了 拉格朗日对偶 的相关知识，使用此方法可以将 支持向量机问题 转换为 拉格朗日对偶问题，从而求解；最后在普遍存在的线性不可分数据集上，我们又做了一个软间隔容许一些样本不满足约束条件，但也要求损失函数达到最小；支持向量回归则是一种回归问题的模型，使用间隔带、损失函数等构建模型，策略和求解的算法都和支持向量机如出一辙。