线性回归(一)基础理论
一、基本概念
设样本 X = ( x ( 1 ) , x ( 2 ) , . . . x ( m ) ) X=(x^{(1)},x^{(2)},...x^{(m)}) X=(x(1),x(2),...x(m)),标签 Y = ( y ( 1 ) , y ( 2 ) , . . . y ( m ) ) Y=(y^{(1)},y^{(2)},...y^{(m)}) Y=(y(1),y(2),...y(m)),上标 i i i表示第 i i i个样本,每个样本是定义在特征空间 x 1 , x 2 , . . x n x_1, x_2,..x_n x1,x2,..xn内的点。而线性回归的目的,在于寻找一个特征空间内的一个最优线性超平面 Θ T x = Σ 1 n θ i x i \Theta^T \boldsymbol{x}=\Sigma_1^n\theta_ix_i ΘTx=Σ1nθixi,使得该超平面到这些样本点的某种距离度量最近。这种思想表现在二维空间内,就是寻找一条最优的直线(如下图)。
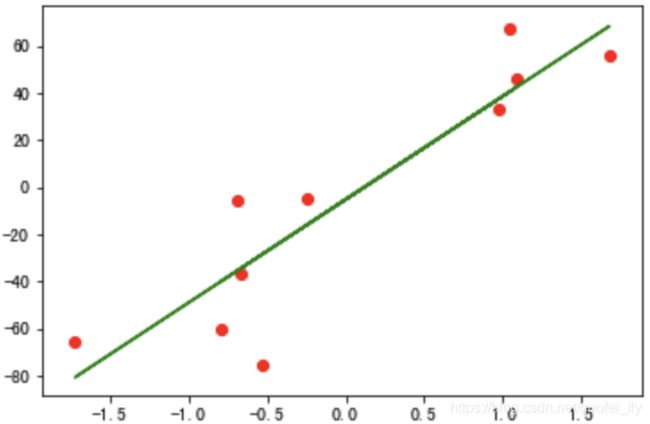
至于这种某种距离度量,很容易想到下面如下策略:
找到某个超平面,样本点在该超平面上的投影值,即预测值,作为真实值值的近似,通过最优化预测值和真实值之间的误差均方差,以求得最优的超平面参数。

这种通过求超平面投影值的方法在感知机、PCA、LDA、SVM中屡试不爽。
二、线性回归与仿射变换
回到线性超平面的数学定义: f ( x ; Θ ) = Θ T x = Σ 1 n θ i x i f(\boldsymbol x;\Theta)=\Theta^T \boldsymbol{x}=\Sigma_1^n\theta_ix_i f(x;Θ)=ΘTx=Σ1nθixi,这是一个典型线性变换,具有拉伸、旋转和降维(当某些 θ i \theta_i θi为0时)等变换形式。注意到线性变换都是相对于绝对坐标原点的变换,而在回归过程中可能需要对超平面进行整体平移,即偏置项。在二维空间内,体现为直线的截距。
因此,线性超平面可进一步写成 f ( x ; Θ ) = Θ T x + b = Σ 0 n θ i x i f(\boldsymbol x;\Theta)=\Theta^T \boldsymbol{x}+b=\Sigma_0^n\theta_ix_i f(x;Θ)=ΘTx+b=Σ0nθixi,其中 x i ≡ 0 x_i\equiv0 xi≡0。这是典型的仿射变换(线性变换+平移)!也就是说,线性回归的目的在于找到一个合适的仿射变换,尽可能的保留原始数据中的信息。
值得一提的是:从向量矩阵的角度来看,放射变换相当于在原 Y = X Θ Y=X\Theta Y=XΘ的特征维度里增加一个维度进行线性变换,再取原来维度上的数据,即 [ Y 0 ] = [ X 1 0 0 ] ∗ [ Θ b ] \begin{bmatrix}Y\\0\end{bmatrix}=\begin{bmatrix}X&1\\0&0\end{bmatrix}*\begin{bmatrix}\Theta\\b\end{bmatrix} [Y0]=[X010]∗[Θb]。
这种线性空间内的维度先改变、再复原的操作在相似矩阵、SVD分解等操作中处处可见。
三、线性回归的两种求解思路
线性回归采用了 min ∣ ∣ X Θ − Y ∣ ∣ 2 \min{||X\Theta-Y||_2} min∣∣XΘ−Y∣∣2作为目标损失函数
3.1 矩阵直接求解 /最小二乘法
损失函数可展开为 L ( Θ ) = ( X Θ − Y ) T ( X Θ − Y ) L(\Theta)=(X\Theta-Y)^T(X\Theta-Y) L(Θ)=(XΘ−Y)T(XΘ−Y)
这是凸函数,其极值处满足 d L ( Θ ) d Θ = 0 \frac{dL(\Theta)}{d\Theta}=0 dΘdL(Θ)=0
d L ( Θ ) = t r ( d L ( Θ ) ) = t r ( d Θ T X T X Θ ) + t r ( Θ T X T X d Θ ) − t r ( d Θ T X T Y ) − t r ( Y T X d Θ ) = t r ( ( ( d Θ ) T X T ) X Θ ) + t r ( Θ T X T X d Θ ) − t r ( ( d Θ ) T X T Y ) − t r ( Y T X d Θ ) = t r ( ( X Θ ) T X D Θ ) + t r ( Θ T X T X d Θ ) − t r ( ( X T Y ) T d Θ ) − t r ( Y T X d Θ ) = 2 t r ( Θ T X T X d Θ ) − 2 t r ( Y T X d Θ ) = t r ( 2 ( Θ T X T X − Y T X ) d Θ ) dL(\Theta)\\=tr(dL(\Theta))\\=tr(d\Theta^TX^TX\Theta)+tr(\Theta^TX^TXd\Theta)-tr(d\Theta^TX^TY)-tr(Y^TXd\Theta)\\=tr(((d\Theta)^TX^T)X\Theta)+tr(\Theta^TX^TXd\Theta)-tr((d\Theta)^TX^TY)-tr(Y^TXd\Theta)\\=tr((X\Theta)^TXD\Theta)+tr(\Theta^TX^TXd\Theta)-tr((X^TY)^Td\Theta)-tr(Y^TXd\Theta)\\=2tr(\Theta^TX^TXd\Theta)-2tr(Y^TXd\Theta)\\=tr(2(\Theta^TX^TX-Y^TX)d\Theta) dL(Θ)=tr(dL(Θ))=tr(dΘTXTXΘ)+tr(ΘTXTXdΘ)−tr(dΘTXTY)−tr(YTXdΘ)=tr(((dΘ)TXT)XΘ)+tr(ΘTXTXdΘ)−tr((dΘ)TXTY)−tr(YTXdΘ)=tr((XΘ)TXDΘ)+tr(ΘTXTXdΘ)−tr((XTY)TdΘ)−tr(YTXdΘ)=2tr(ΘTXTXdΘ)−2tr(YTXdΘ)=tr(2(ΘTXTX−YTX)dΘ)
所以 d L ( Θ ) d Θ = 2 ( Θ T X T X − Y T X ) T = 2 ( X T X Θ − X T Y ) = 0 \frac{dL(\Theta)}{d\Theta}=2(\Theta^TX^TX-Y^TX)^T=2(X^TX\Theta-X^TY)=0 dΘdL(Θ)=2(ΘTXTX−YTX)T=2(XTXΘ−XTY)=0
可得 Θ = ( X T X ) − 1 X T Y \Theta=(X^TX)^{-1}X^TY Θ=(XTX)−1XTY
3.2 梯度下降法求解
直接采用矩阵求解,涉及到矩阵逆运算,计算量较大,所以还可以采用的梯度下降数值方法进行迭代求解。
上文求得: d L ( Θ ) d Θ = 2 ( X T X Θ − X T Y ) \frac{dL(\Theta)}{d\Theta}=2(X^TX\Theta-X^TY) dΘdL(Θ)=2(XTXΘ−XTY)
所以,梯度下降的迭代公式为: Θ : = Θ − 2 α X T ( X Θ − Y ) \Theta:=\Theta-2\alpha X^T(X\Theta-Y) Θ:=Θ−2αXT(XΘ−Y),式中超参数 α \alpha α表示学习率,用来控制下降速度
写成各维度参数 θ j \theta_j θj的形式: θ j : = θ j − α ∗ 2 m Σ i = 1 m ( Θ T ∗ x ( i ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\alpha*\frac{2}{m}\Sigma_{i=1}^m(\Theta^T*x^{(i)}-y^{(i)})x_j^{(i)} θj:=θj−α∗m2Σi=1m(ΘT∗x(i)−y(i))xj(i)
每一次迭代都需要加载全部数据,为了减小运算量,可采用SGD或批量SGD的方法。
四、线性回归背后的原理
4.1 线性回归与正态分布
前文提到,线性回归选择最优超平面时,采用的度量方式为样本点拟合值与真实值的均方差最小。那为什么这种选择是合适的呢?
其实,线性回归中隐藏了误差符合正态分布的这个假设条件,即 ϵ ( i ) = y ( i ) − Θ T x ( i ) ∼ N ( μ , σ 2 ) \epsilon^{(i)} = y^{(i)}-\Theta^Tx^{(i)} \sim N(\mu, \sigma^2) ϵ(i)=y(i)−ΘTx(i)∼N(μ,σ2)
每个样本的误差概率为:
P ( ϵ ( i ) ) = 1 2 π σ e x p ( − ( ϵ ( i ) − μ ) 2 2 σ 2 ) P(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\epsilon^{(i)}-\mu)^2}{2\sigma ^2}) P(ϵ(i))=2πσ1exp(−2σ2(ϵ(i)−μ)2)
代入数据和参数,可写成:
P ( y ( i ) ; Θ , x ( i ) ) = 1 2 π σ e x p ( − ( Θ T x ( i ) − μ ) 2 2 σ 2 ) P(y^{(i)};\Theta,x^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\Theta^Tx^{(i)}-\mu)^2}{2\sigma ^2}) P(y(i);Θ,x(i))=2πσ1exp(−2σ2(ΘTx(i)−μ)2)
假设各样本满足独立同分布条件(IID),则整个数据集上的似然函数为:
L ( Θ ) = ∏ i = 1 m P ( y ( i ) ; Θ , x ( i ) ) = ( 1 2 π σ ) m ∏ i = 1 m e x p ( − ( Θ T x ( i ) − μ ) 2 2 σ 2 ) L(\Theta)=\prod_{i=1}^{m}P(y^{(i)};\Theta,x^{(i)})=(\frac{1}{\sqrt{2\pi}\sigma})^m \prod_{i=1}^{m}exp(-\frac{(\Theta^Tx^{(i)}-\mu)^2}{2\sigma ^2}) L(Θ)=i=1∏mP(y(i);Θ,x(i))=(2πσ1)mi=1∏mexp(−2σ2(ΘTx(i)−μ)2)
取对数似然函数:
l n L ( Θ ) = m l n ( 1 2 π σ ) + Σ i ( − ( Θ T x ( i ) − μ ) 2 2 σ 2 ) lnL(\Theta)=mln(\frac{1}{\sqrt{2\pi}\sigma})+\Sigma_i(-\frac{(\Theta^Tx^{(i)}-\mu)^2}{2\sigma ^2}) lnL(Θ)=mln(2πσ1)+Σi(−2σ2(ΘTx(i)−μ)2)
根据MLE,取 m a x ( l n L ( Θ ) ) max (lnL(\Theta)) max(lnL(Θ)),即取 m i n ( Σ i ( Θ T x ( i ) − μ ) 2 ) min(\Sigma_i(\Theta^Tx^{(i)}-\mu)^2) min(Σi(ΘTx(i)−μ)2),即为最小化预测方差。
综上,线性回归可视为建立在误差符合正态分布基础上的最大似然估计。
4.2 RMSE的数学意义
在线性回归中,均方差MSE和均方根RMSE不仅为优化问题的损失函数,也被视为模型的评价指标。那求得的RMSE具体表示什么意义的?
回一下正态分布的图形:数据位于期望值 μ \mu μ两侧 σ , 2 σ , 3 σ \sigma,2\sigma,3\sigma σ,2σ,3σ区间的概率分别为68%,95%和97%。
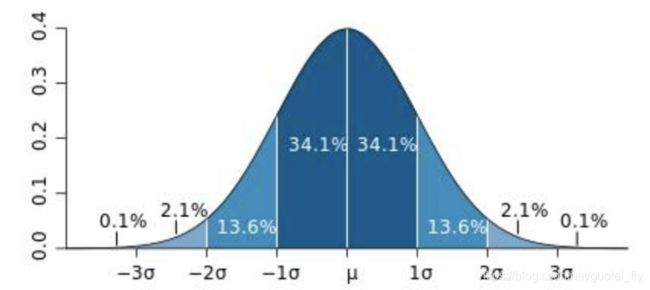
而RMSE也正表达了这个含义:68%/95%/99.7%的预测系统预测值与真实值的偏差分别位于1RMSE、2RMSE和3RMSE区间内。
五、正则化
线性回归作为一种线性模型,可通过正则化手段来抑制过拟合现象。在线性回归基础上广泛采用的正则化策略有:
(1)基于L1正则化的Lasso回归
损失函数为 J ( Θ ) = ∣ ∣ X Θ − Y ∣ ∣ 2 + α ∣ ∣ Θ ∣ ∣ 1 J(\Theta)=||X\Theta-Y||_2+\alpha||\Theta||_1 J(Θ)=∣∣XΘ−Y∣∣2+α∣∣Θ∣∣1
(2)基于L2正则化的岭回归
损失函数为 J ( Θ ) = ∣ ∣ X Θ − Y ∣ ∣ 2 + β ∣ ∣ Θ ∣ ∣ 2 J(\Theta)=||X\Theta-Y||_2+\beta||\Theta||_2 J(Θ)=∣∣XΘ−Y∣∣2+β∣∣Θ∣∣2
(3)基于L1正则化和L2正则化加权的弹性弹性网络
损失函数为 J ( Θ ) = ∣ ∣ X Θ − Y ∣ ∣ 2 + α ∣ ∣ Θ ∣ ∣ 2 + β ∣ ∣ Θ ∣ ∣ 1 J(\Theta)=||X\Theta-Y||_2+\alpha||\Theta||_2+\beta||\Theta||_1 J(Θ)=∣∣XΘ−Y∣∣2+α∣∣Θ∣∣2+β∣∣Θ∣∣1
六、总结
线性回归作为一种简单的线性模型,是各类广义线性模型(如逻辑回归、线性SVM等)的基础,与PCA、LDA等降维算法也颇有渊源。其背后隐藏着的矩阵运算、统计学假设和方法也值得多加体会。