WISE 2019 | ML-GCN:多标签图节点分类的半监督图嵌入
目录
- 前言
- 1. 回顾GCN
-
- 1.1 GCN原理
- 1.2 GCN的缺点
- 2. ML-GCN
-
- 2.1 Skip-Gram
- 2.2 ML-GCN思想
- 2.3 协同优化和负采样
- 3. 实验
前言

题目: Semi-supervised Graph Embedding for Multi-label Graph Node Classification
会议: International Conference on Web Information Systems Engineering 2019
论文地址:Semi-supervised Graph Embedding for Multi-label Graph Node Classification
之前的文章中有讲到GCN可以用作图的节点分类,并且给出了代码实现,具体可以参考:
- ICLR 2017 | GCN:基于图卷积网络的半监督分类
- PyG搭建GCN前的准备:了解PyG中的数据格式
- PyG搭建GCN实现节点分类(GCNConv参数详解)
GCN通过图卷积层来集成节点、节点特征以及图拓扑关系来生成节点的状态向量,进而将其应用于节点分类等具体任务。对于简单的多标签分类任务来讲,GCN将图的特征矩阵经过多个图卷积层后得到每个节点的状态向量表示,然后再经过一个softmax函数来进行分类,最后再最小化softmax输出与真实标签的交叉熵损失。这种处理方式比较简单,但也容易丢失一些信息,如标签之间的相关性,从而无法得到较好的预测性能。
鉴于此,本文作者提出了新的基于GCN的半监督节点分类器:ML-GCN。具体来讲,ML-GCN首先使用GCN来嵌入节点特征和图形拓扑信息。然后随机生成一个标签矩阵,其中每一行(即标签向量)代表一种标签。标签向量的维数与GCN最后一次卷积操作前的节点向量维数相同。也就是说,所有的标签和节点都嵌入在一个统一的向量空间中。最后,在ML-GCN的模型训练过程中,将标签向量和节点向量连接起来作为skip-gram的输入,以检测节点-标签的相关性以及标签-标签的相关性。
值得注意的是,这篇论文提出的ML-GCN不是大家认为的由旷视研究院提出ML-GCN(基于图卷积网络的多标签图像识别模型),不过二者的思想是一致的,都是对标签间的依赖性进行建模。
1. 回顾GCN
ML-GCN是基于GCN的,因此本文就先回忆一下GCN的具体处理过程,这部分内容在之前的文章中已经详细讲解过,具体请见:ICLR 2017 | GCN:基于图卷积网络的半监督分类。
1.1 GCN原理
给定一个无向图 G = ( V , E , X , Y ) G=(V,E,X,Y) G=(V,E,X,Y),其中 V = ( V l ∪ V u ) V=(V_l \cup V_u) V=(Vl∪Vu), v l v_l vl和 v u v_u vu分别表示带标签的节点和不带标签的节点, n = n l + n u n=n_l+n_u n=nl+nu表示节点数目,在半监督学习中,一般不带标签的节点为大多数,我们的任务是推导出这些节点的标签; E E E为边集; x ∈ R n × d x \in R^{n\times d} x∈Rn×d表示节点特征矩阵;标签矩阵 Y ∈ R n l × c Y \in R^{n_l \times c} Y∈Rnl×c一共 n l n_l nl行,为01矩阵, c c c表示标签的总类别数; A ∈ R n × n A\in R^{n \times n} A∈Rn×n为邻接矩阵; D = d i a g ( d 1 , d 2 , . . . , d n ) D=diag(d_1,d_2,...,d_n) D=diag(d1,d2,...,dn)为度矩阵。
因此,对称归一化拉普拉斯矩阵可以定义为: L s y m = I − D − 1 2 A D − 1 2 L_{sym}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}} Lsym=I−D−21AD−21。
GCN每一层的操作可以定义为:
H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) H^{(l+1)}=\sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) H(l+1)=σ(D~−21A~D~−21H(l)W(l))
其中 A ~ = A + I \tilde{A}=A+I A~=A+I表示带自环的邻接矩阵, I I I为单位矩阵。 D ~ \tilde{D} D~为加上自环后的度矩阵; W ( l ) W^{(l)} W(l)为层权重矩阵; σ ( ⋅ ) \sigma(\cdot) σ(⋅)为激活函数,比如ReLU; H ( 0 ) = X H^{(0)}=X H(0)=X,也就是节点特征矩阵;经过多层卷积后,我们得到了最终的 H k H^{k} Hk, H k H^{k} Hk即GCN学到的节点的状态向量表示。
假设经过最后一层图卷积后得到了 H ( l + 1 ) H^{(l+1)} H(l+1),为了实现分类任务,我们可以加上一个sigmoid层:

这里 H ( l + 1 ) ∈ R n × c H^{(l+1)}\in R^{n \times c} H(l+1)∈Rn×c,每一行表示一个节点的各个标签的概率。最后,最小化结果与标签矩阵 Y Y Y的交叉熵损失:

1.2 GCN的缺点
上述GCN模型简单易懂,但这种简单的模型可能存在一些问题:
- 如果我们使用较少的层来构造GCN,那么最后一层维度与倒数第二层维度之间的差异可能会非常大,这可能会造成隐藏特征的丢失,使模型难以优化。例如Citeseer引文网络,它的输入特征维数为3703,标签数量为6,如果我们使用双层GCN,无论隐藏层维数的设置如何,我们都不能让维数平滑下降。
- 如果我们简单地堆叠更多的层,该模型将混合来自不同标签的节点的特性,使它们难以区分。
- 具有sigmoid层的多标签分类模型不能捕获标签关系,因为它单独处理每个标签。因此,它可能会丢失关于多标签图数据集的一些信息。
为了解决上述问题,本文提出了一个新的基于GCN的多标签节点分类模型ML-GCN。
2. ML-GCN
2.1 Skip-Gram
鉴于本文需要用到skip-gram的知识,因此这里简单回归一下。
假设窗口长度为w=2,单词序列为: w 1 , w 2 , w 3 , w 4 , w 5 {w1, w2, w3, w4, w5} w1,w2,w3,w4,w5,我们的目标是使得以下概率最大化:
P ( w 1 , w 2 , w 4 , w 5 ∣ w 3 ) P(w1,w2,w4,w5|w3) P(w1,w2,w4,w5∣w3)
我们假设预测间是相互独立的,即我们需要最大化:
P ( w 1 ∣ w 3 ) P ( w 2 ∣ w 3 ) P ( w 4 ∣ w 3 ) P ( w 5 ∣ w 3 ) P(w1|w3)P(w2|w3)P(w4|w3)P(w5|w3) P(w1∣w3)P(w2∣w3)P(w4∣w3)P(w5∣w3)
因此,假设上下文长度为 c c c,中心词为 w t w_t wt,那么上述优化目标可以被表示为:
∏ t = 1 T ∏ − c ≤ j ≤ c , j ≠ 0 P ( w t + j ∣ w t ) \prod_{t=1}^{T} \prod_{-c\leq j \leq c, j \neq0}P(w_{t+j}|w_t) t=1∏T−c≤j≤c,j=0∏P(wt+j∣wt)
考虑到:如果一个概率较小,连乘后概率会非常小的问题,对上述概率进行对数处理:
∑ t = 1 T ∑ − c ≤ j ≤ c , j ≠ 0 l o g P ( w t + j ∣ w t ) \sum_{t=1}^{T} \sum_{-c\leq j \leq c, j \neq0}log\ P(w_{t+j}|w_t) t=1∑T−c≤j≤c,j=0∑log P(wt+j∣wt)
其中 T T T表示文本长度。
在skip-gram中,假设当前中心词为 c c c,要预测的上下文词语为 w w w,那么上述概率可以表示为:
P ( w ∣ c ; θ ) = e x p ( u w T v c ) ∑ i ∈ V u i T v c P(w|c;\theta)=\frac{exp(u_w^T v_c)}{\sum_{i \in V}u_{i}^Tv_c} P(w∣c;θ)=∑i∈VuiTvcexp(uwTvc)
其中 u u u和 v v v可以理解为一开始初始化的两个参数矩阵,也就是参数 θ \theta θ的组成部分,这两个矩阵的维度都为 R ∣ V ∣ × d R^{|V| \times d} R∣V∣×d,也就是词库中每个单词的嵌入向量表示。其中矩阵 v v v可以理解为中心词矩阵,矩阵 u u u为上下文矩阵。简单来说,就是将中心词向量与所有上下文词向量的内积运算做softmax,进而得到某个特定上下文单词 w w w出现的概率。
上述公式的内在逻辑为:如果两个单词越相似,那么它们的词向量就越相似,那么内积就越大,概率也就越大。最大化概率,也就是最大化中心词向量与其上下文词向量的相似性。
具体训练步骤:
- 将所有单词进行one-hot编码,每个单词编码后的长度为 ∣ V ∣ |V| ∣V∣。
- 将所有单词经过中心词矩阵 v v v得到其长度为 d d d的向量表示,即 R ∣ V ∣ × d R^{|V| \times d} R∣V∣×d。
- 初始化一个权重矩阵 u u u,维度同样为 R ∣ V ∣ × d R^{|V| \times d} R∣V∣×d,也就是前面提到的上下文矩阵。
- 取出中心词的词向量 v c ∈ R 1 × d v_c \in R^{1 \times d} vc∈R1×d,然后与上下文矩阵中的所有向量做内积运算,这里也包括了单词 w w w的向量,此时我们可以得到 V V V个数字,然后进行softmax运算,以得到概率。
- 对所有单词都求出其概率,然后概率之和最大化,利用梯度下降法反向更新上述两个矩阵。
2.2 ML-GCN思想
ML-GCN与GCN最大的不同在于其引入了一个标签嵌入矩阵 Z Y ∈ R c × l Z_Y \in R^{c\times l} ZY∈Rc×l,即将每一个类的标签都表示为一个长度为 l l l的向量。标签向量矩阵一开始是随机初始化的,这里的 l l l与最后一次图卷积运算前的维度一致。假设最后一层卷积的输出为 H ( l + 1 ) H^{(l+1)} H(l+1),那么 H ( l ) ∈ R n × l H^{(l)} \in R^{n \times l} H(l)∈Rn×l。
下图给出了ML-GCN的具体框架:

由上图可知,原始图一共有7个节点,那么假设 X ∈ R 7 × s X \in R^{7 \times s} X∈R7×s,经过第一层卷积后,变成 R 7 × 5 R^{7 \times 5} R7×5,也就是上面提到的 H ( l ) H^{(l)} H(l),然后我们随机初始化 Z Y ∈ R 3 × 5 Z_Y \in R^{3 \times 5} ZY∈R3×5,也就是一共三个类别。然后,利用 Z Y Z_Y ZY计算label-label损失,同时结合 H ( l ) H^{(l)} H(l)计算node-label损失。最后,将 H ( l ) H^{(l)} H(l)经过第二层卷积,得到最终的图卷积结果并计算交叉熵损失。
上面的描述只是一个大概的框架,接下来我们进行详细的说明。
考虑一个具有多个标签的节点,我们的目标是最大化给定节点的这些标签出现的概率,输入为节点向量和对应的标签向量。如果我们将一个节点及其标签视为一个句子,那么目标可以被描述为:给定一个中心单词(节点),进而预测临近单词(标签),这是skip-gram的基本思想,即:根据中心词以预测其上下文词语。例如,如下图所示:
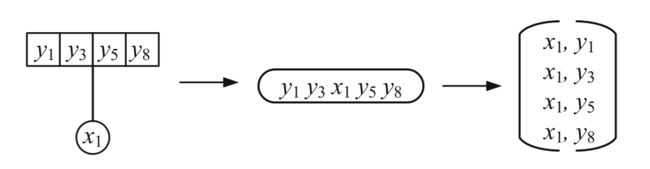
节点 x 1 x_1 x1具有4个标签,我们可以将节点和标签都视为单词以生成一个句子,然后我们利用skip-gram进行计算。
现在将skip-gram引入到节点标签句子中:给定节点 x i x_i xi及其标签 Y x i = y 1 , y 2 , . . . , y c Y_{x_i}={y_1,y_2,...,y_c} Yxi=y1,y2,...,yc,此时 x i x_i xi的向量表示为 H ( l ) H^{(l)} H(l)的第 i i i行, y j y_j yj的标签向量为 z y j z_{y_j} zyj,我们考虑节点 x i x_i xi作为中心词,其标签作为上下文词语。由于各个标签间没有顺序关系,因此我们可以组成 c c c个label-node对,即上图所示。
对于任意一个节点 x i x_i xi,我们通过最大化以下函数来优化节点及其标签嵌入:
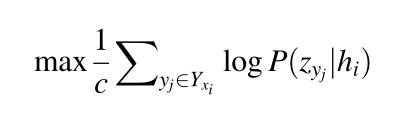
即最大化节点与其标签共现的对数概率。
经过上述处理后,我们可以在特征维降至标签类之前更好地在高维空间捕获node-label相关性。
参考上述思想,我们可以捕获label-label相关性。具体来讲,给定节点 x i x_i xi及其标签 Y x i = y 1 , y 2 , . . . , y c Y_{x_i}={y_1,y_2,...,y_c} Yxi=y1,y2,...,yc,不同于前面最大化节点与标签共现的概率,在这里我们最大化标签与标签之间共现的概率,即:

对于某一个节点来说,如果该节点只有一个label,那么我们只考虑计算node-label相关性,如果该节点有多个label,那么我们可以同时考虑node-label相关性和label-label相关性。
2.3 协同优化和负采样
如果标签类数过多,上述计算将变得十分复杂,因此可以考虑使用负采样。
对于nodel-label相关性,我们可以考虑将其从:
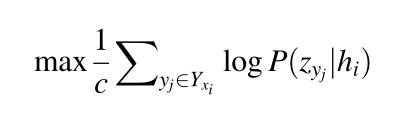
变为:

这里 K K K为超参数,即需要采样的node-label个数。
对于label-label相关性,同样可以变为:

因此,ML-GCN的整体流程可以描述如下:

假设一共需要训练 n n n轮,对其中每一轮:
- 将节点的特征向量矩阵经过多个GCNConv层,以得到最终的状态向量表示 H ( l + 1 ) H^{(l+1)} H(l+1)。
- 将 H ( l + 1 ) H^{(l+1)} H(l+1)经过一个sigmoid函数,再与标签计算交叉熵损失。
- 计算经过负采样后的node-label损失。
- 计算经过负采样后的label-label损失。
- 将三个损失进行加权,然后利用Adam优化加权损失。
3. 实验
数据集:
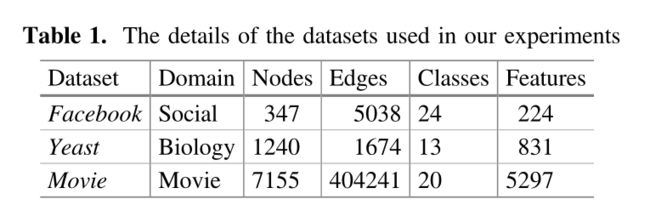
实验结果:

其中,Partly ML-GCN为只计算node-label损失的ML-GCN。可以发现,ML-GCN效果是最好。