深入理解图卷积神经网络(GCN)原理
深入理解图卷积神经网络(GCN)原理
文章目录
- 深入理解图卷积神经网络(GCN)原理
- 前言
- 一、为什么需要GCN
- 二、GCN的原理
-
- 1.图的定义
- 2.GCN来了
-
- 2.1 矩阵计算公式
- 2.2 以小规模矩阵讲解公式含义
- 2.3 综上所述:
- 三、GCN有多牛
- 总结
前言
深度学习的发展日新月异,从经典的深度网络(DNN、CNN、RNN)到GAN、强化学习。深度学习覆盖的应用场景越来越丰富。今天介绍的图神经网络是另一类深度学习方法。虽然,图神经网络也可以纳入深度学习的范畴,但它有着自己独特的应用场景和算法实现,对初学者并不算太友好。GCN,全称Graph Convolutional Network,图卷积网络,本文主要实现对GCN的深入理解,帮助快速理解GCN的原理以及用途。
一、为什么需要GCN
卷积神经网络(CNN)的输入是图片等具有欧几里得结构的图结构,也就是这样的图:

从欧式空间里面利用卷积核(kernel)来提取特征,因为图片是比较规则的图结构,因此使用卷积核就可以平移提取节点特征,即CNN的核心在于它的kernel,kernel是一个个小窗口,在图片上平移,通过卷积的方式来提取特征。这里的关键在于图片结构上的平移不变性:一个小窗口无论移动到图片的哪一个位置,其内部的结构都是一模一样的,因此CNN可以实现参数共享。这就是CNN的精髓所在。但是通常我们会遇到拓扑网络或者社交网络,即如下
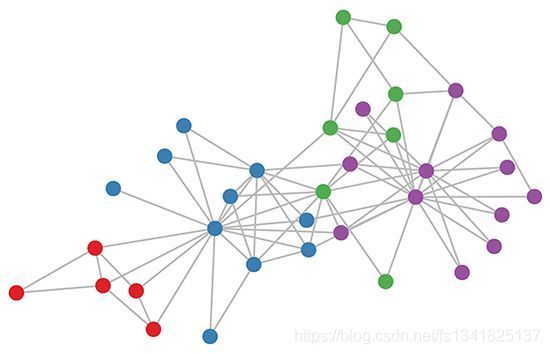
像这种图结构,并不整齐,一个网络包含不同数量的节点,不同的节点也包含不同的邻居,这使得传统的CNN无法作用在该图结构中,并且图中的每个node之间通常具有联系,因此当GCN问世,解决了这一难题。
二、GCN的原理
1.图的定义
图结构用G=(V,E)来表示,图包括有向图或者无向图,但是在GCN中只考虑无向图,V表示node的几何,E表示edge的几何,n表示的是node的数量,m则表示边的个数。
下面我们介绍一个图结构在GCN中各种符号表示的含义:
G = ( V , E ) 表 示 当 前 图 结 构 v i ∈ V 表 示 v i 是 一 个 n o d e e i j = ( e i , e j ) ∈ E 表 示 n o d e i 与 j 之 间 的 边 N ( v ) = { u ∈ V ∣ ( v , u ) ∈ E } 表 示 点 v 的 所 有 邻 居 集 合 A i j 表 示 图 的 邻 接 矩 阵 A i j = 1 表 示 n o d e i 和 j 之 间 存 在 边 D 表 示 当 前 图 的 度 矩 阵 , D 是 对 角 矩 阵 d i i ∈ D 表 示 A 中 每 个 节 点 的 度 X ∈ R n × d 表 示 n 个 节 点 的 特 征 向 量 , 特 征 向 量 维 度 是 d G=(V,E) \qquad 表示当前图结构 \\v_i\in V\qquad表示v_i是一个node \\e_{ij}=(e_i,e_j)\in E\qquad表示node\quad i与j之间的边 \\N(v)=\{u\in V|(v,u)\in E\}\qquad表示点v的所有邻居集合 \\A_{ij}\qquad表示图的邻接矩阵 \\A_{ij}=1\qquad表示node\quad i和j之间存在边 \\D\qquad 表示当前图的度矩阵,D是对角矩阵 \\d_{ii}\in D\quad 表示A中每个节点的度 \\X\in R^{n\times d}表示n个节点的特征向量,特征向量维度是d G=(V,E)表示当前图结构vi∈V表示vi是一个nodeeij=(ei,ej)∈E表示nodei与j之间的边N(v)={u∈V∣(v,u)∈E}表示点v的所有邻居集合Aij表示图的邻接矩阵Aij=1表示nodei和j之间存在边D表示当前图的度矩阵,D是对角矩阵dii∈D表示A中每个节点的度X∈Rn×d表示n个节点的特征向量,特征向量维度是d
2.GCN来了

GCN神奇的地方在于,能够聚合一个node附近的node特征,通过加权聚合学习到node的feature从而去做一系列的预测任务。
2.1 矩阵计算公式
假设我们手头有一批图数据,其中有n个节点(node),每个节点都有自己的feature向量,我们设这些节点的特征组成一个n×d维的特征矩阵X,然后各个节点之间的关系也会形成一个 n × n n\times n n×n维的邻接矩阵A。X和A便是我们模型的输入。
对于所有node而言,即 H ( l ) H^{(l)} H(l)表示当所有阶段在l层的特征向量矩阵, H ( l + 1 ) H^{(l+1)} H(l+1)表示所有经过一次卷积操作之后的特征向量矩阵。一次卷积操作的公式如下:
H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right) H(l+1)=σ(D~−21A~D~−21H(l)W(l))
A ^ = A + I \hat{A}=A+I A^=A+I
在这个公式中:
- A + I A+I A+I, I I I是单位矩阵,即对角线为1,其余全为0
- D ~ \tilde{D} D~是 A ~ \tilde{A} A~的度矩阵,计算方法 D ~ = ∑ A ~ i j \tilde{D}=\sum{\tilde{A}_{ij}} D~=∑A~ij
- H H H是每一层的所有节点的特征向量矩阵,对于输入层的话, H ( 0 ) H^{(0)} H(0)就等于 X X X, [ n , d ] [n,d] [n,d]维度
- σ是非线性激活函数,如 R E L U RELU RELU
- W ( l ) W^{(l)} W(l)表示的是当前层卷积变换的可训练的参数矩阵
其实就是实现了对图中每个node的邻居node进行加权求和,利用与参数矩阵相乘得到新一层的node的特征。
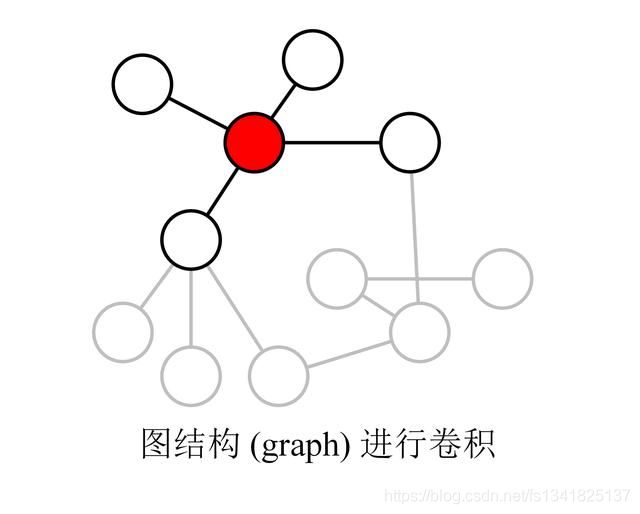
利用矩阵的形式迭代计算每个node的特征,然后通过层传播进行卷积操作,最后更新node的特征。
2.2 以小规模矩阵讲解公式含义
公式是从矩阵的角度计算,那为什么要这么复杂的矩阵形式呢,首先我们用最简单的矩阵计算来看看
H ( l + 1 ) = f ( H ( l ) , A ) = σ ( A H ( l ) W ( l ) ) H ( 0 ) = X ∈ R n × d \begin{array}{c} H^{(l+1)}=f\left(H^{(l)}, A\right)=\sigma\left(A H^{(l)} W^{(l)}\right) \\ H^{(0)}=X \in R^{n \times d} \end{array} H(l+1)=f(H(l),A)=σ(AH(l)W(l))H(0)=X∈Rn×d
上面的公式中 W为卷积变换的参数,可以训练优化。A 矩阵为邻接矩阵,Aij 不为 0 则表示节点 i,j 为邻居,ij存在边。H 为所有节点的特征向量矩阵,每一行是一个节点的特征向量,H(0) 就是 X 矩阵。A 和 H 的乘积其实就是把所有的邻居节点向量进行相加,如下图所示,表示 A × H A\times H A×H。
[ 0 1 1 0 1 0 0 0 1 0 0 1 0 0 1 0 ] [ 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 ] = [ 5 5 5 5 5 1 1 1 1 1 5 5 5 5 5 3 3 3 3 3 ] \left[\begin{array}{cccc} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 2 & 2 \\ 3 & 3 & 3 & 3 & 3 \\ 4 & 4 & 4 & 4 & 4 \end{array}\right]=\left[\begin{array}{ccccc} 5 & 5 & 5 & 5 & 5 \\ 1 & 1 & 1 & 1 & 1 \\ 5 & 5 & 5 & 5 & 5 \\ 3 & 3 & 3 & 3 & 3 \end{array}\right] ⎣⎢⎢⎡0110100010010010⎦⎥⎥⎤⎣⎢⎢⎡12341234123412341234⎦⎥⎥⎤=⎣⎢⎢⎡51535153515351535153⎦⎥⎥⎤
A A A表示的是邻接矩阵, H H H表示的是4个node,每个node有一个5维的feature向量,将 A 和 H A和H A和H直接相乘会得到右边矩阵AH的结果。得到 AH 之后再和 W训练参数 相乘,最后经过激活函数 σ 就得到下一层4个node的特征向量了。
但是上面的公式存在一些问题, A H AH AH 只获得了某个节点的邻居信息,而忽略了节点本身信息。为了解决这个问题,我们可以将矩阵 A A A中对角线的值设为 1,即每个节点会指向自身,新的卷积公式如下:
H ( l + 1 ) = σ ( A ~ H ( l ) W ( l ) ) A ~ = A + I n \begin{aligned} H^{(l+1)} &=\sigma\left(\tilde{A} H^{(l)} W^{(l)}\right) \\ \tilde{A} &=A+I_{n} \end{aligned} H(l+1)A~=σ(A~H(l)W(l))=A+In
I为单位矩阵,即对角线为 1,其余为 0。即使用上面的卷积公式即可把节点自身的信息也考虑进去,但是这个公式仍然存在问题:矩阵 A 没有归一化,AH 会把节点所有邻居的向量都相加,这样经过多层卷积后某些节点的特征向量的值会很大。因为邻接矩阵没有被规范化,这在提取图特征时可能存在问题,比如邻居节点多的节点倾向于有更大的特征值。
通常使用对称归一化的方法:
归一化的意思就是在聚合一个node节点的邻居节点特征时
A = D − 1 2 A D − 1 2 A i j = A i j d i d j \begin{array}{l} A=D^{-\frac{1}{2}} A D^{-\frac{1}{2}} \\ A_{i j}=\frac{A_{i j}}{\sqrt{d_{i}} \sqrt{d_{j}}} \end{array} A=D−21AD−21Aij=didjAij
2.3 综上所述:
我们首先为了考虑A中所有node的自身特征,将 A A A加上 I I I变成 A ~ \tilde{A} A~,然后为了考虑在聚合node的邻居节点特征的时候会出现特征向量不断相加导致邻居节点更多的节点特征更大的现象,我们使用了对称归一化。
这样一来就能得到GCN的层传播公式, H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right) H(l+1)=σ(D~−21A~D~−21H(l)W(l))
以一个二层的GCN为例
A ^ = D ~ − 1 2 A ~ D ~ − 1 2 Z = softmax ( A ^ ReLu ( A ^ X W ( 0 ) ) W ( 1 ) ) \begin{array}{c} \hat{A}=\widetilde{D}^{-\frac{1}{2}} \tilde{A} \widetilde{D}^{-\frac{1}{2}} \\ Z=\operatorname{softmax}\left(\hat{A} \operatorname{ReLu}\left(\hat{A} X W^{(0)}\right) W^{(1)}\right) \end{array} A^=D −21A~D −21Z=softmax(A^ReLu(A^XW(0))W(1))
GCN 可以用最后一层卷积层得到的节点特征向量进行预测,即最后一层输出层要用softmax操作,前面的0层到1层的非线性激励函数采用的 R e L u ReLu ReLu。
三、GCN有多牛
在看了上面的公式以及训练方法之后,GCN好像并没有什么特别之处,但是结合GCN论文中所贴出来的结果,原来GCN这么牛,在原数据中同类别的node,经过GCN的提取出的embedding,已经在空间上自动聚类了
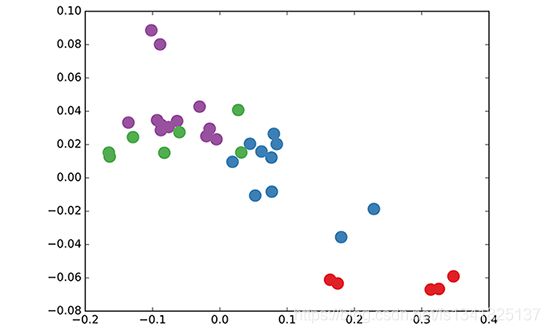
深入探究GCN为什么这么强的原因其实正是考虑到了图中每一个node的邻居关系,这与传统的CNN是不同的,并且在其背后的数学公式之美也值得我们研究,具体的深究GCN公式计算请参考如何理解 Graph Convolutional Network(GCN)
总结
至此,我们已经深入理解了GCN的相关概念,其实就是利用图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡,关系越亲近的邻居影响越大。 node之间通过互相影响以及W参数矩阵的训练,最终学习到每一个node的特征。
同时GCN的层数也不宜过多,**简单说就是gcn层数多了会使得每个点的embedding比较相近,这样子对于后面的节点分类等loss函数不利,**当然可以通过各种normalize来抵消一些影响。从热力学角度看啊,每个节点embedding看作是节点温度,gcn每次卷积可以看作是每个节点和周围节点在做热量交换。在没有外部热量源的条件下(节点没有额外的标签label),如果图是全联通的,多次卷积最后就会使得每个节点的温度,也就是embedding变成一样的。
下篇文章我们将讨论使用DGL实现GCN以及GAT的引入。