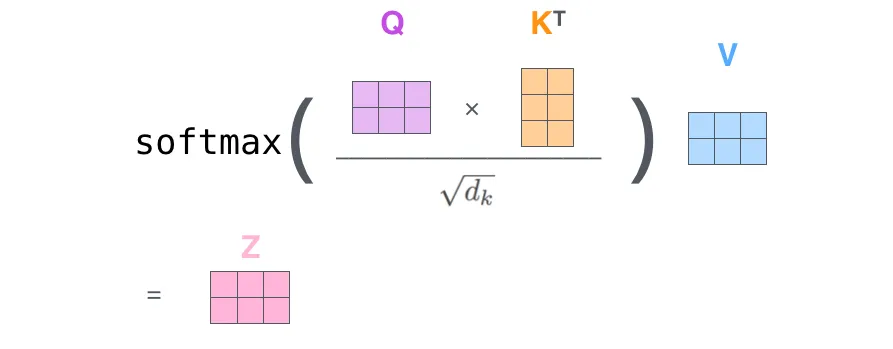【论文阅读】Attention Is All You Need
【论文阅读】Attention Is All You Need
前言
Transformer 是谷歌在 2017 年底发表的论文 Attention Is All You Need 中所提出的 seq2seq 模型,Transformer 的提出也给 NLP 领域带来了极大震动。现如今,不少模型还是以 Transformer 作为特征抽取机制 ,比如 BERT 就是从 Transformer 中衍生出来的预训练语言模型。
Overview
Transformer 完全抛弃了传统的 CNN 和 RNN,整个网络结构完全是由 Attention 机制组成。作者认为 RNN 的固有的按照顺序进行计算的特点,限制了并行计算能力,即 RNN 只能是从左向右或是从右向左依次进行计算。
{% note info no-icon %}
Transformer 和 RNN 的最大区别,就是 RNN 是迭代的、串行的,必须要等当前字处理完,才可以处理下一个字。而 Transformer 模型的训练是并行的,大大增加了计算的效率。
{% endnote %}
另一方面,作者在编码词向量时引入了 Position coding,即在词向量中加入了单词的位置信息,用来更好地理解语言的顺序。
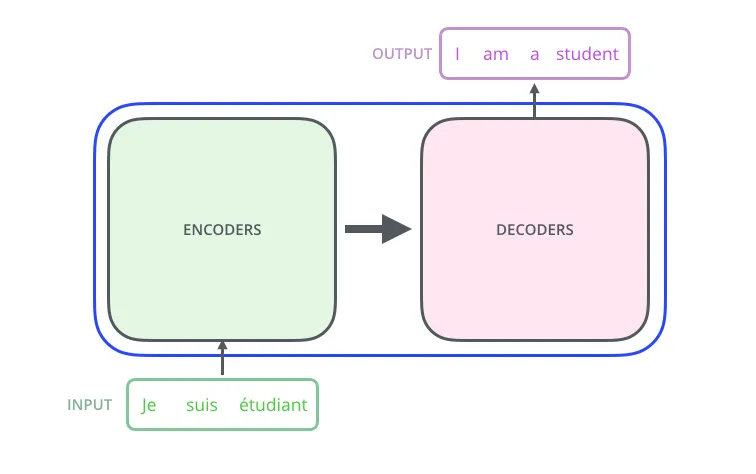
Transformer 由 Encoder 和 Decoder 两个部分组成,其中 Encoder 负责将输入(自然语言序列)变换为隐藏层特征,Decoder 负责将隐藏层特征还原为自然语言序列。
{% note success no-icon %}
以机器翻译为例,如下图所示,通过将待翻译文本按顺序进行 Encoder 和 Decoder 之后,最终得到翻译文本:
{% endnote %}
Transformer Encoder
在对模型的结构有了大概了解之后,我们再仔细看看模型的具体的内部特征。
Model Architecture
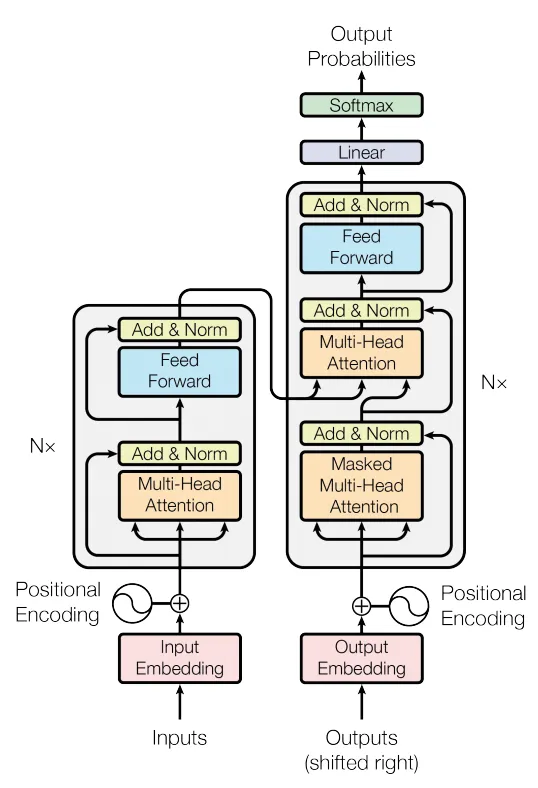
按照上面的模型架构图我们可以把模型分为两部分,左半边为 Encoder,右半边为 Decoder。需要注意的是,并不是仅仅通过一层的 Encoder 和 Decoder 就得到输出,而是要分别经过 N N N层,在论文中这个数字是 N = 6 N=6 N=6。
Encoder:Encoder 由 N = 6 N=6 N=6个完全相同的层堆叠而成。每一层都有两个子层,从下到上依次是:Multi-Head Attention和Feed Forward,对每个子层再进行残差连接和标准化。
Decoder:Decoder 同样由 N = 6 N=6 N=6个完全相同的层堆叠而成。每一层都有三个子层,从下到上依次是:Masked Multi-Head Self-Attention、Multi-Head Attention和Feed Forward,同样的对每个子层再进行残差连接和标准化。
接下来我们按照模型结构的顺序逐个进行说明。
Position Encoding
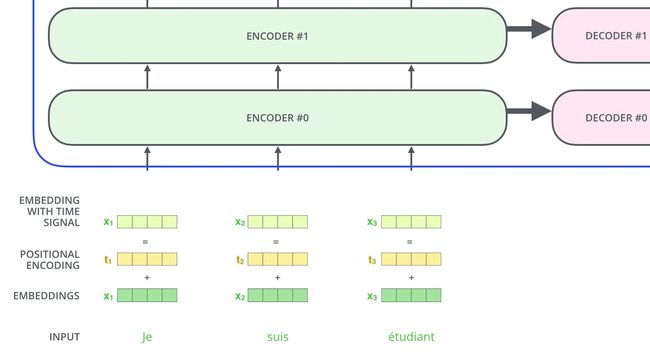
就像之前提到的,Transformer 中抛弃了传统的 CNN 和 RNN,并没有类似迭代的操作,这就意味着 Transformer 本身不具备捕捉顺序序列的能力。为了解决这个问题,论文中在编码词向量时引入了位置编码,即Positional Encoding(PE),将字符的绝对或者相对位置信息注入。
如下图所示,论文在经过 Embedding 之后,又将其与 Position Encoding 直接相加(注意:不是拼接而是简单的对应位置直接相加)
Positional Encoding 可以通过训练得到,也可以使用某种公式计算得到。论文中使用了 sin 和 cos 函数的线性变换来提供给模型位置信息:
P E ( p o s , 2 i ) = sin ( p o s / 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = cos ( p o s / 1000 0 2 i / d m o d e l ) \begin{aligned} PE_{(pos, 2i)} &= \sin (pos/10000^{2i/d_{model}}) \\ PE_{(pos,2i+1)} &= \cos (pos/10000^{2i/d_{model}}) \end{aligned} PE(pos,2i)PE(pos,2i+1)=sin(pos/100002i/dmodel)=cos(pos/100002i/dmodel)
其中 p o s pos pos表示一句话中单词的位置, i i i是词向量维度序号, d m o d e l d_{model} dmodel是词向量维度。
{% folding green open, 关于 Positional Encoding 的一些问题 %}
在论文中,使用 sin 和 cos 函数的线性变换来提供位置信息,但具体为什么这么设计直接看公式还是有些难理解的。
如果让我们来设计一个简单的 Positional Encoding,一个最简单直观的方法就是 P E = p o s l e n g t h − 1 PE=\frac{pos}{length - 1} PE=length−1pos,对每个词的位置进行线性的分配,但实际上这个方法并不可行。举个例子,某句话的长度为 10,另一句话的长度为 100,对编码位置作差,对于同样的差值,包含的意义确实完全不同的,即在两句话中间隔的字符数量明显不相同。
简而言之,理想的编码需要满足一下条件:
- 对于每个位置的词语,它都能提供一个独一无二的编码
- 词语之间的间隔对于不同长度的句子来说,含义应该是一致的
- 它的值应该是有界的
我们将公式转换一下形式:
p t ⃗ ( i ) = f ( t ) ( i ) : = { sin ( ω k ⋅ t ) , if i = 2 k cos ( ω k ⋅ t ) , if i = 2 k + 1 \vec{p_t}^{(i)} = f(t)^{(i)} := \begin{cases} \sin (\omega_k \cdot t), &\text{if } i=2k \\ \cos (\omega_k \cdot t), &\text{if } i=2k+1 \end{cases} pt(i)=f(t)(i):={sin(ωk⋅t),cos(ωk⋅t),if i=2kif i=2k+1
其中
ω k = 1 1000 0 2 k / d \omega_k = \frac{1}{10000^{2k/d}} ωk=100002k/d1
具体来说,一个词的 Positional Encoding 是这样表示的:
p t ⃗ = [ sin ( w 1 t ) cos ( w 2 t ) ⋯ sin ( w d / 2 t ) cos ( w d / 2 t ) ] d × 1 \vec{p_t} = \begin{bmatrix}\sin(w_1t) \\ \cos(w_2t) \\ \cdots \\ \sin(w_{d/2}t) \\ \cos(w_{d/2}t) \end{bmatrix}_{d \times 1} pt=⎣⎢⎢⎢⎢⎡sin(w1t)cos(w2t)⋯sin(wd/2t)cos(wd/2t)⎦⎥⎥⎥⎥⎤d×1
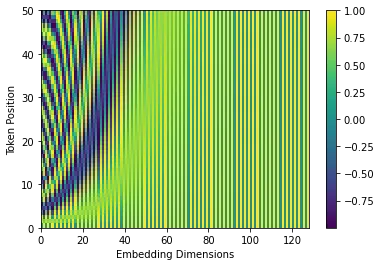
我们知道, k k k是不断变大的,因此 ω k \omega_k ωk越来越小,因此频率 ω k 2 π \frac{\omega_k}{2\pi} 2πωk也越来越小,这也就意味着随着 k k k词向量维度序号的增大,该位置的数字的变化频率是指数级下降的。
下图展示了 Positional Encoding 具体编码过程:
画图代码如下:
import numpy as np
import matplotlib.pyplot as plt
def get_angles(pos, i, d_model):
angle_rates = 1 / np.power(10000, (2 * (i // 2)) / np.float32(d_model))
return pos * angle_rates
def positional_encoding(position, d_model):
angle_rads = get_angles(
np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :], d_model)
# apply sin to even indices in the array; 2i
angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
# apply cos to odd indices in the array; 2i+1
angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
pos_encoding = angle_rads[np.newaxis, ...]
return pos_encoding
tokens, dimensions = 50, 128
pos_encoding = positional_encoding(tokens, dimensions)
plt.pcolormesh(pos_encoding[0], cmap='viridis')
plt.xlabel('Embedding Dimensions')
plt.ylabel('Token Position')
plt.colorbar()
plt.show()
{% endfolding %}
Self Attention
对于输入句子,我们首先进行 Word Embedding,之后又经过 Positional Encoding 之后,最后我们得到了带有位置信息的词向量,记为 x t x_t xt。
之后就是最关键的 Self Attention 部分,Attention 的核心内容是为输入句子的每个单词学习一个权重,你甚至可以简单的理解为加权求和。
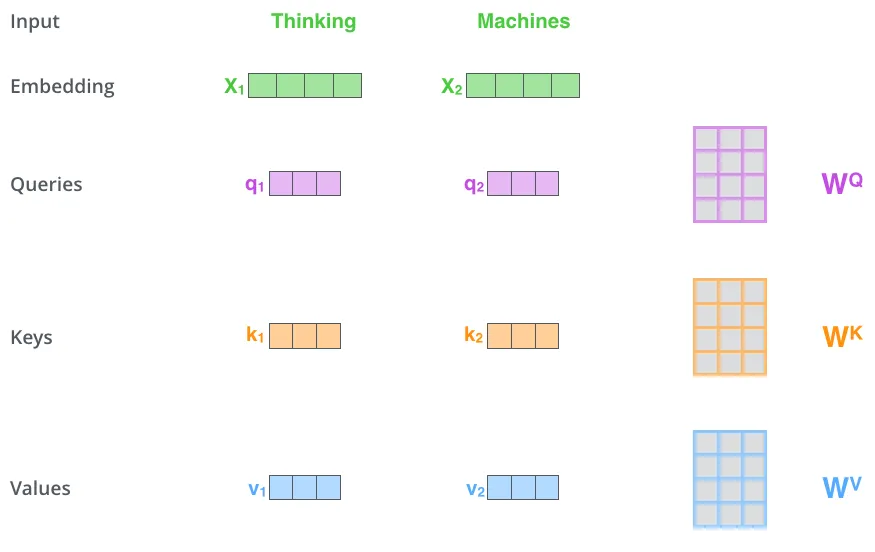
具体来说,我们需要为每个词向量 x t x_t xt准备三个向量 q t , k t , v t q_t,k_t,v_t qt,kt,vt。将所有词向量的 q t , k t , v t q_t,k_t,v_t qt,kt,vt拼接起来,我们就可以得到一个大矩阵,分别记为查询矩阵 Q Q Q,键矩阵 K K K,值矩阵 V V V(在模型训练时,这三个矩阵都是需要学习的参数)。
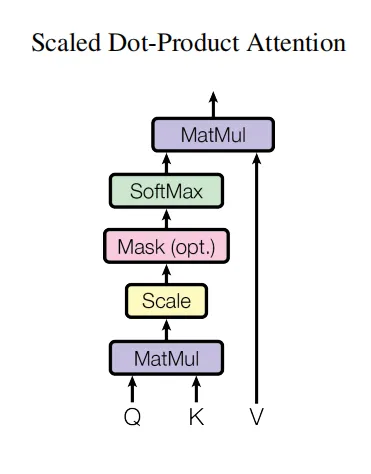
之后根据 Q , K , V Q,K,V Q,K,V计算:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^{T}}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
关于这个公式的详细解读你可以参考我的另一篇文章 Self Attention 详解。
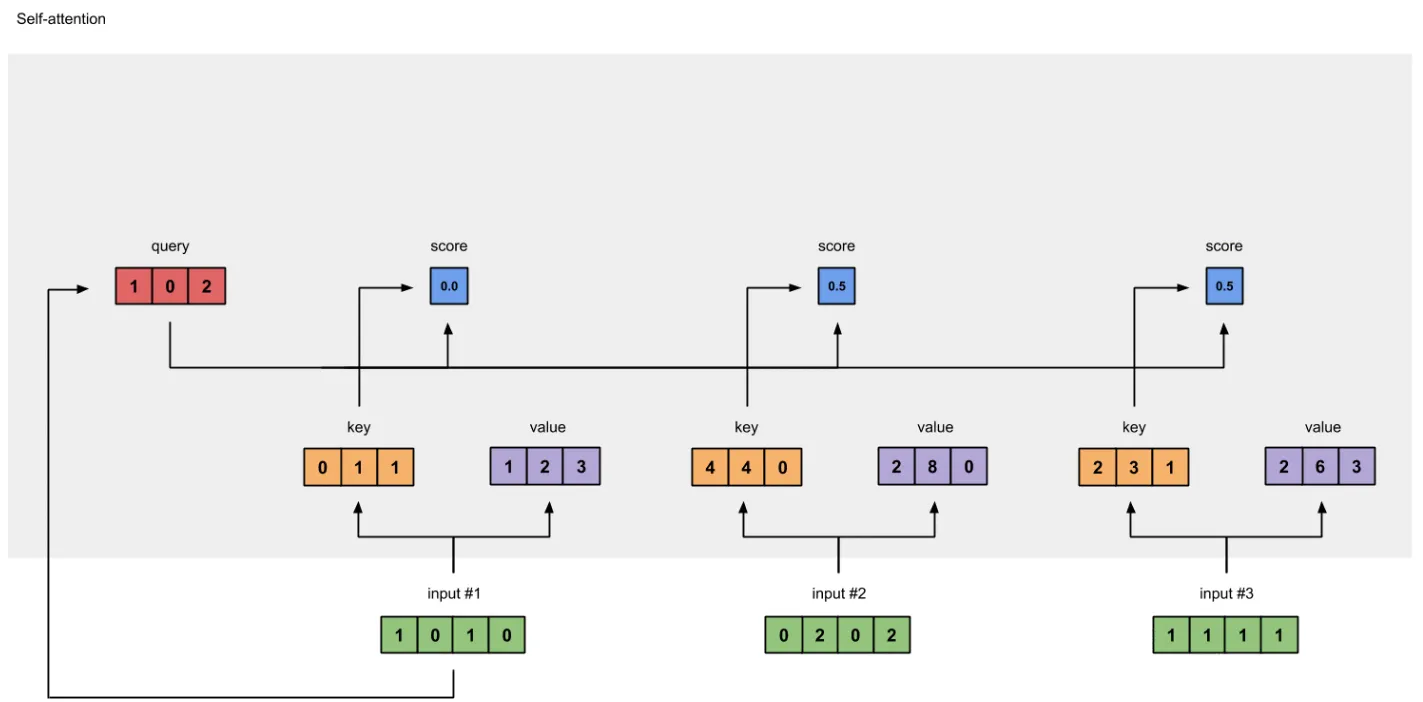
{% folding green open, 计算 Attention 的一个例子 %}
(以下图片来自 mathor)
每个词向量 x t x_t xt,假设我们已经有了 q t , k t , v t q_t,k_t,v_t qt,kt,vt和查询矩阵 Q Q Q,键矩阵 K K K,值矩阵 V V V,现在我们来计算具体的输出:
首先是第一步,为了获得第一个字的注意力权重,我们需要用第一个字的查询向量 q 1 q_1 q1 乘以键矩阵 K
[0, 4, 2]
[1, 0, 2] x [1, 4, 3] = [2, 4, 4]
[1, 0, 1]
之后还需要将得到的值经过 softmax,使得它们的和为 1
softmax([2, 4, 4]) = [0.0, 0.5, 0.5]
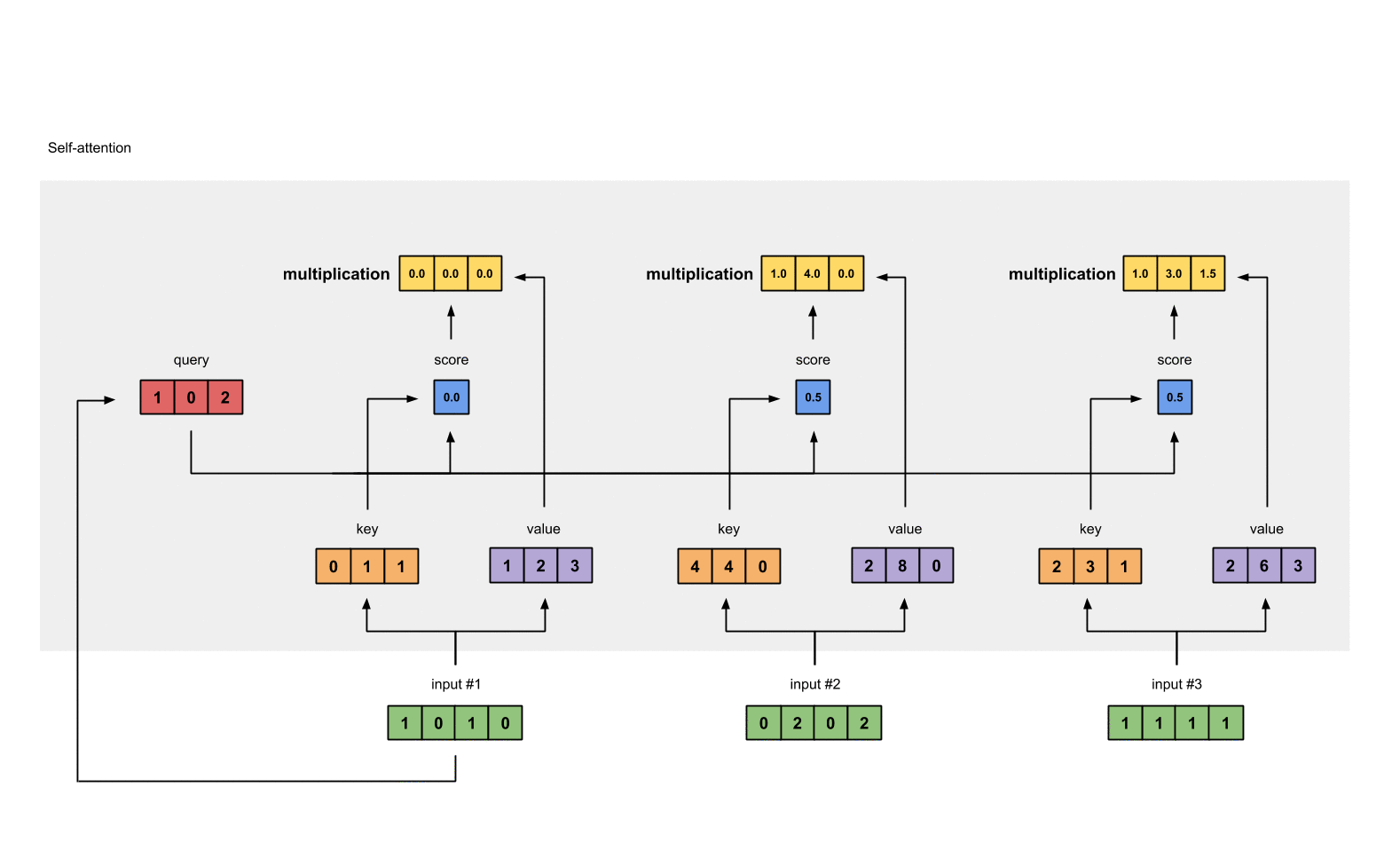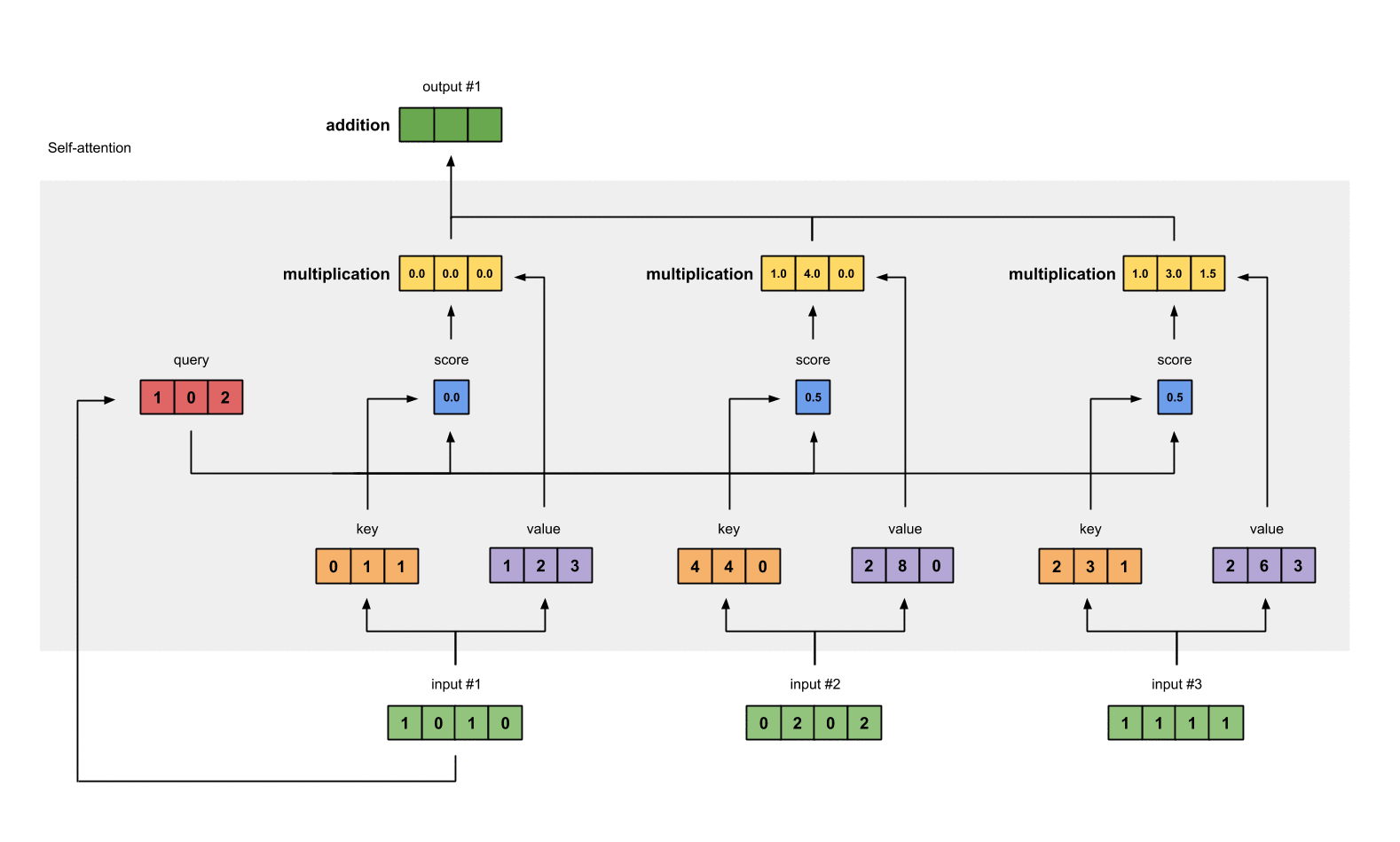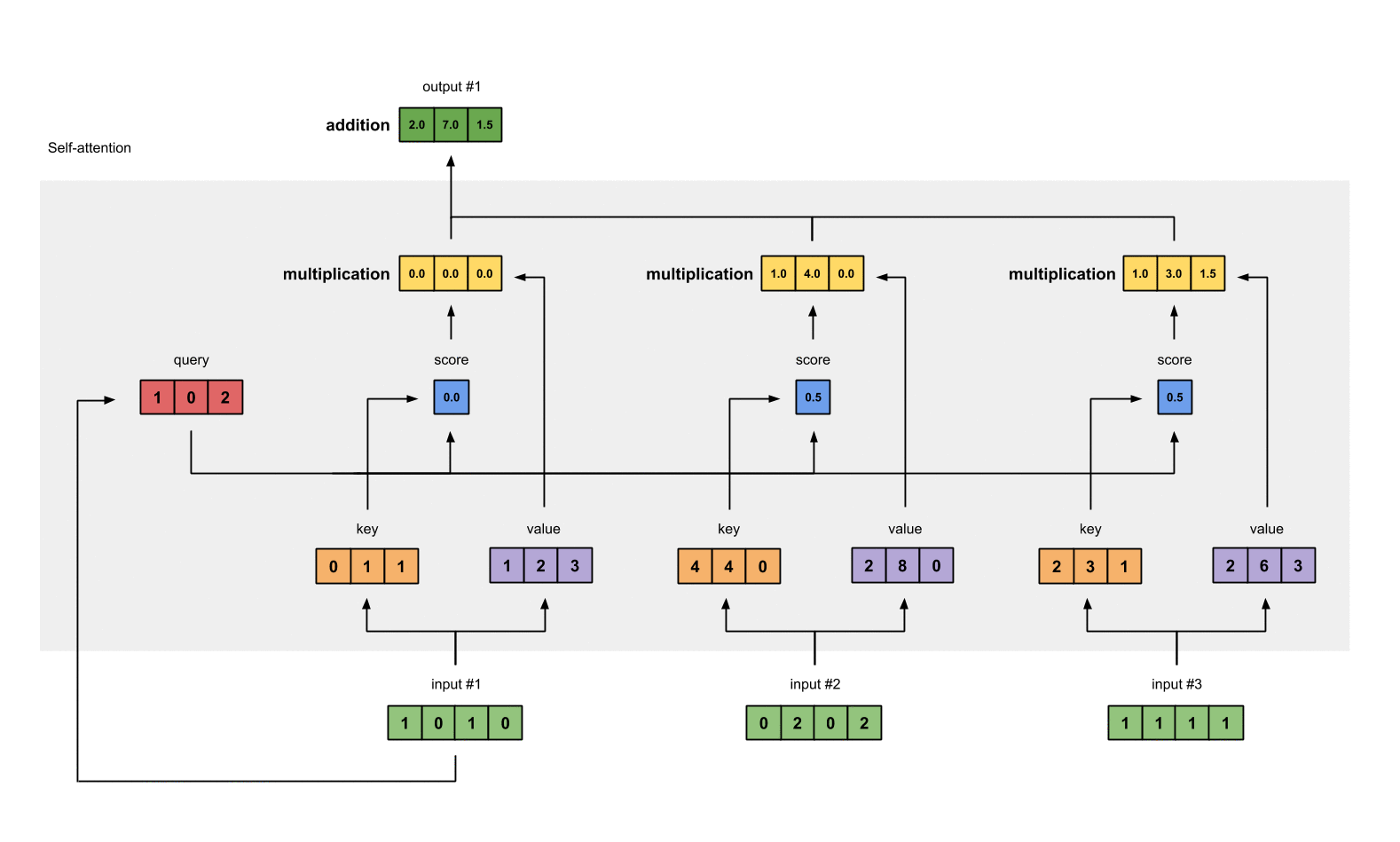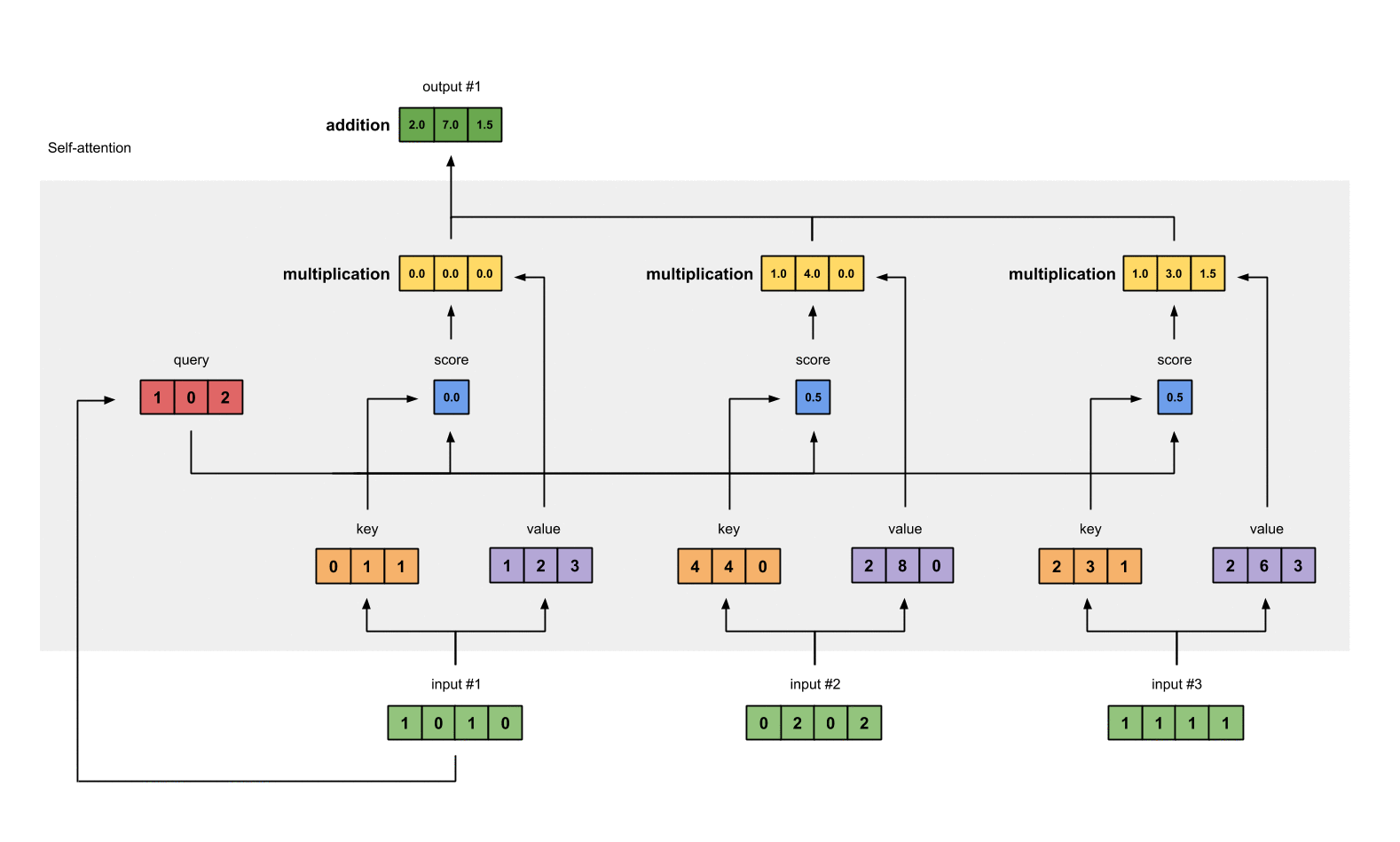
有了权重之后,将权重其分别乘以对应字的值向量 v t v_t vt
0.0 * [1, 2, 3] = [0.0, 0.0, 0.0]
0.5 * [2, 8, 0] = [1.0, 4.0, 0.0]
0.5 * [2, 6, 3] = [1.0, 3.0, 1.5]
最后将这些权重化后的值向量求和,得到第一个字的输出
[0.0, 0.0, 0.0]
+ [1.0, 4.0, 0.0]
+ [1.0, 3.0, 1.5]
-----------------
= [2.0, 7.0, 1.5]
对其它的输入向量也执行相同的操作,即可得到通过 self-attention 后的所有输出
{% endfolding %}
在上面的例子中,你只需要把向量变成矩阵的形式,就可以一次性得到所有输出,这也正是 Attention 公式所包含的具体意义:
Multi-Head Attention
同时,论文又进一步提出了 Multi-Head Attention 的概念。简而言之,就是 h h h个 Self Attention 的集成。在 Self Attention 中,我们通过定义一组 Q , K , V Q,K,V Q,K,V来对上下文进行学习,而 Multi-Head Attention 就是通过定于多组 Q , K , V Q,K,V Q,K,V,分别对不同位置的上下文进行学习:
MultiHead ( Q , K , V ) = Concat ( head 1 , ⋯ , head h ) W O w h e r e head i = Attention ( Q W i Q , K W i K , V W i V ) \begin{aligned} \text{MultiHead}(Q,K,V) &= \text{Concat}(\text{head}_1, \cdots, \text{head}_h)W^O \\ where \text{head}_i &= \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \end{aligned} MultiHead(Q,K,V)whereheadi=Concat(head1,⋯,headh)WO=Attention(QWiQ,KWiK,VWiV)
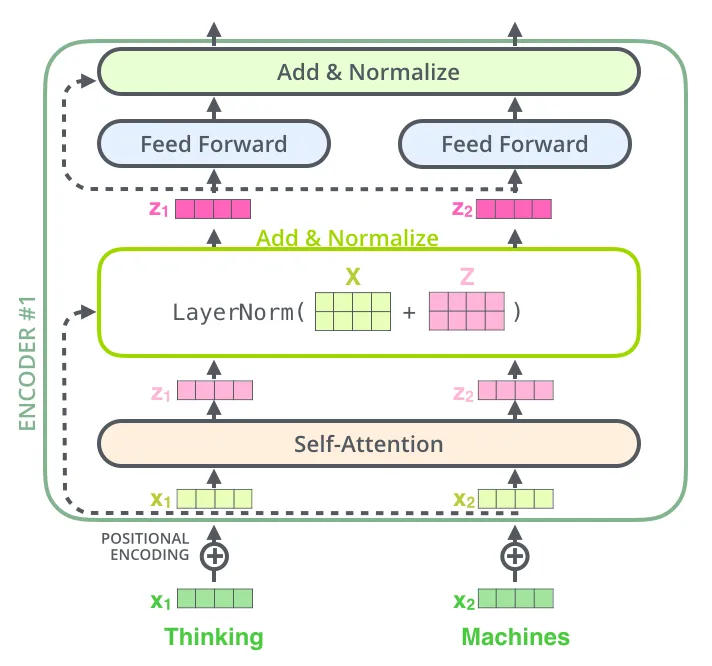
Add & Norm
在 Add & Norm 层中,分为两部分:残差连接和标准化。下图展示了具体的细节:
残差连接
残差连接将输出表述为输入和输入的一个非线性变换的线性叠加,通常用于解决多层网络训练的问题:
具体来说在 Transformer 中则是:
X E m b e d d i n g + Self-Attention ( Q , K , V ) X_{Embedding} + \text{Self-Attention}(Q,K,V) XEmbedding+Self-Attention(Q,K,V)
标准化
Norm指 Layer Normalization,将隐藏层归一为标准正态分布,以加速收敛。
Feed Forward
Feed Forward 层比较简单,是一个两层的全连接网络,第一层的激活函数是 ReLU,第二层无激活函数:
FFN ( X ) = max ( 0 , X W 1 + b 1 ) W 2 + b 2 \text{FFN}(X)=\max(0,XW_1+b_1)W_2+b_2 FFN(X)=max(0,XW1+b1)W2+b2
Transformer Encoder 整体结构
经过上面各个部分的解读,我们基本了解了 Encoder 的主要构成部分,现在简单做个小结:
-
生成词向量并进行位置编码
X = Embedding ( X ) + Positional-Encoding ( X ) X=\text{Embedding}(X)+\text{Positional-Encoding}(X) X=Embedding(X)+Positional-Encoding(X)
-
自注意力机制
X attention = Self-Attention ( Q , K , V ) = softmax ( Q K T d k ) V X_{\text{attention}}=\text{Self-Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V Xattention=Self-Attention(Q,K,V)=softmax(dkQKT)V
-
残差连接与标准化
X attention = L a y e r N o r m ( X + X attention ) X_{\text{attention}}=LayerNorm(X+X_{\text{attention}}) Xattention=LayerNorm(X+Xattention)
-
Feed Forward
FFN ( X attention ) = max ( 0 , X attention W 1 + b 1 ) W 2 + b 2 \text{FFN}(X_{\text{attention}})=\max(0,X_{\text{attention}}W_1+b_1)W_2+b_2 FFN(Xattention)=max(0,XattentionW1+b1)W2+b2
-
残差连接与标准化
X attention = L a y e r N o r m ( X + X attention ) X_{\text{attention}}=LayerNorm(X+X_{\text{attention}}) Xattention=LayerNorm(X+Xattention)
-
将输出送入 Decoder
Transformer Decoder
Transformer 的 Decoder block 结构,与 Encoder block 相似,但还是存在一些区别:
- 包含两个 Multi-Head Attention 层。
- 第一个 Multi-Head Attention 层采用了 Masked 操作。
- 第二个 Multi-Head Attention 层的 K , V K,V K,V使用 Encoder 的输出, Q Q Q使用上一个 Decoder block 的输出计算。
- 最后使用 softmax 计算下一个词的概率。
Masked Multi-Head Attention
Masked Multi-Head Attention 这里的 Masked 简而言之就是对数据进行遮挡,那么为什么要进行这个操作呢?
在进行 decoder 时,模型的输入是包含全部单词的所有信息的,但是对于翻译任务而言,它的流程是顺序进行的,即处理完第 i i i个单词之后,才可以处理第 i + 1 i+1 i+1个单词,这也就意味着在处理第 i i i个单词的时候,模型是不应该知道第 i i i个单词之后的信息的,否则就是信息泄露了。因此,这里进行 Mask 的作用就是对这部分信息进行遮挡。
Decoder Multi-Head Attention
第二个 Multi-Head Attention 层的结构与前面讲的基本相同,唯一的不同就是 K , V K,V K,V使用 Encoder 的输出, Q Q Q使用上一个 Decoder block 的输出计算,后续的计算方法与之前描述的一致。
softmax
最后的最后,就是进行 softmax,输出概率最高的单词。
PyTorch 实现
EmoryHuang/nlp-tutorial
总结
整体来说,Transformer 的结构还是非常巧妙的,完全抛弃了 CNN 和 RNN,仅仅使用 Self-Attention 进行特征提取,并且还做到了更好的效果。更可贵的是,各种基于 Transformer 架构的模型仍层出不穷,在各个领域均得到了用武之地。
参考资料
- [1] Attention Is All You Need
- Transformer 详解
- The Illustrated Transformer