算法手札二:红黑树的插入原理，原理与实现篇

• 红黑树的五大性质(性质四与性质五特别重要)

1. 节点必须是红色或者是黑色

2. 根节点是黑色的

3. 所有的叶子节点是黑色的。

4. 每个红色节点的两个子节点是黑色的，也就是不能存在父子两个节点全是红色。

5. 从任意每个节点到其每个叶子节点的所有简单路径上黑色节点的数量是相同的。

       以下情况两点说明:

1. 新节点是红孩子
2. 二叉树的左分支来讨论，右分支相反即可

• 第0种情况：

       如果，父亲节点是黑色的，那么，直接插入即可！(如图)

//Segement 1

void RB_Insert_Case0(Node *node)

{

     if( node -> parent -> color == RB_BLACK)

     {

        return;//树是有效的

     }

     else

     {

        RB_Insert_Case1(node);

     }

}

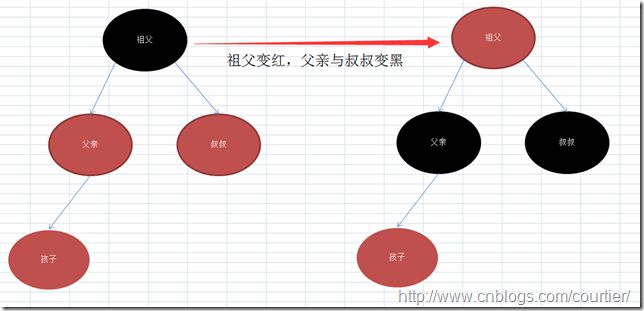
• 第一种情况：

       如果，父亲节点是红色的，它的叔叔是红色的，那么，直接把祖父变成红色，然后，父亲与叔叔变成黑色！(如图)

 

//Segement 2

void RB_Insert_Case1(Node *node)

{

     Noude *uncle = getUncle()node);

     if( uncle!=null && uncle->color == RB_RED)

     {

        uncle->color = RB_BLACK;

        node->paren->color = RB_BLACK;

        uncle->parent = RB_RED;//GrandParent

        init();//所有函数调用完必须重新把root改为黑色. 

     }

     else

     {

        RB_Insert_Case2(node);

     }

}

• 第二种情况：

       如果，父亲节点是红色的，它的叔叔是黑色的，那么，新节点是右孩子，则先左旋，变成第三种情况！(如图)

//Segement 3

void RB_Insert_Case2(Node *node)

{

     if(  node->paren->rchild == node)

     {

        Rb_Rotate_Left(node->paren);

        init();//所有函数调用完必须重新把root改为黑色. 

     }

       RB_Insert_Case3(node);

}

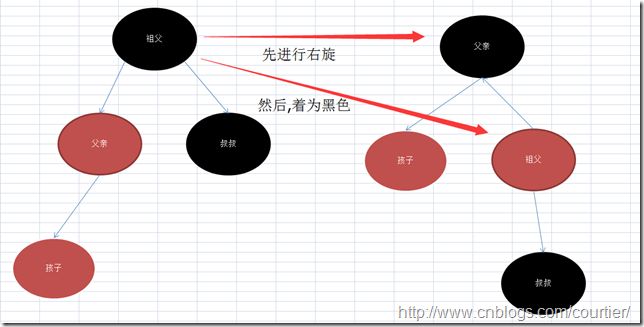
• 第三种情况：

       如果，父亲节点是红色的，它的叔叔是黑色的，那么，节点是左孩子，则进行以（祖父的节点）向右转！(如图)

void RB_Insert_Case3(Node *node)

{

        Node *parent = node->parent;

        Node *grandp = parent -> parent;

        parent -> color = RB_RED;

        grandp  -> color = RB_RED;

        Rb_Rotate_Right(grandp);

  

        init();//所有函数调用完必须重新把root改为黑色.

}

• 结束语

       红黑树，是个伟大的算法，我一直对这个算法保持着高度的尊敬，因为，太高效了，我们可以有个简单证明，把红黑树的红节点合并到黑节点

       就会出现2-3-4树，从而得出一个公式2^h≤n+1≤4^h，而且，可以根据性质4得知树的高度最多是2h，而h=lg(n+1)(刚才的公式取对数)最

       坏的情况都是对数，可见其好处！可以见到应用于：stl的set map java的set map!

       有错误请指出，转载请注明，谢谢!O(∩_∩)O