DGL中的消息传递相关内容的讲解
文章目录
- 前言
- 消息传递范式
-
- DGL中的自定义消息函数
- DGL中的自定义聚合函数
- DGL中的自定义更新函数
- 实例分析
-
- 创建图
- 消息传递
- graph.apply_edges
- 参考
前言
学会DGL中的消息传递,基本就能够比较好的来理解编写各种图神经网络的代码了吧。
消息传递范式
消息传递是实现GNN的一种通用框架和编程范式。它从聚合与更新的角度归纳总结了多种GNN模型的实现。

因此在DGL代码编写消息传递部分时,我们需要三个函数,分别是消息函数、聚合函数、更新函数。
简单来说就是:
消息函数用来取边和节点的特征。
聚合函数用来计算边和节点的特征,例如特征求和,根据特征求个注意力权重等等。
更新函数用来更新节点的特征,对聚合函数传来的特征可以过个激活函数等,最后得到最终的节点特征即可更新。
DGL中的自定义消息函数
在DGL中,消息函数 接受一个参数 edges,这是一个 EdgeBatch 的实例, 在消息传递时,它被DGL在内部生成以表示一批边。 edges 有 src、 dst 和 data 共3个成员属性, 分别用于访问源节点、目标节点和边的特征。
用法就是定义一个函数,然后需要传入一个edges参数,这个参数有src、 dst 和 data 共3个成员属性,能够索引对应的特征
例:
def message_func(edges):
print("-"*20)
print("edges.data[x]", edges.data["x"]) # 获得边的特征
print("edges.src[x]", edges.src["x"]) # 获得边的源节点的特征
print("edges.dst[x]", edges.dst["x"]) # 获得边的目标节点的特征
# 返回得到需要传递的消息特征
return {'e_data': edges.src['h'], "e_src": edges.src["x"], "e_dst": edges.dst["x"]}
DGL中的自定义聚合函数
聚合函数 接受一个参数 nodes,这是一个 NodeBatch 的实例, 在消息传递时,它被DGL在内部生成以表示一批节点。 nodes 的成员属性 mailbox 可以用来访问节点收到的消息。 一些最常见的聚合操作包括 sum、max、min 等。
用法就是定义一个函数,然后需要传入一个nodes参数,这个参数能够通过mailbox索引消息函数return来的特征。
例:
def reduce_func(nodes):
print("+"*20)
# 获取每个节点的边特征的和并储存在节点的e_data中
data_sum = th.sum(nodes.mailbox["e_data"], dim=1)
# 获取每条边的源节点特征并求和储存在节点的src_data中
src_sum = th.sum(nodes.mailbox["e_src"], dim=1)
# 获取每条边的目标节点特征并求和储存在节点的src_data中
dst_sum = th.sum(nodes.mailbox["e_dst"], dim=1)
print("nodes_e_data", data_sum)
print("nodes_e_src", src_sum)
print("nodes_e_dst", dst_sum)
return {"data_sum":data_sum, "src_sum":src_sum, "dst_sum":dst_sum}
DGL中的自定义更新函数
更新函数 同样接受参数 nodes。此函数对聚合函数的聚合结果进行操作, 通常在消息传递的最后一步将其与节点的特征相结合,并将输出作为节点的新特征。
例:
def apply_node_func(nodes):
# 将x用data_sum更新
return {'x': nodes.data["data_sum"]}
最后加上
g.update_all(message_func, reduce_func, apply_node_func)
即可完成消息传递的操作。
实例分析
创建图
首先我们先创建那么一张图:
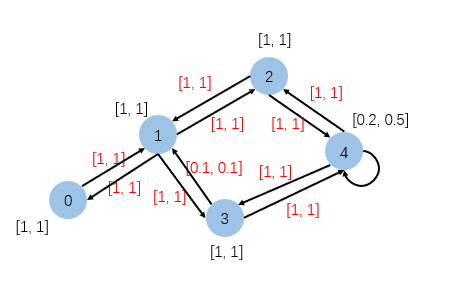
其中黑色的为节点的特征,红色的为边的特征
对应创建代码如下:
import dgl
import dgl.function as fn
import torch
import torch as th
# 构建图
g = dgl.graph(([0, 1, 1, 1, 2, 3, 2, 4, 3, 4, 4], [1, 0, 3, 2, 1, 1, 4, 2, 4, 3, 4]))
# 每个节点的特征都为[1, 1]
g.ndata['x'] = torch.ones(5, 2)
# 每边节点的特征都为[1, 1]
g.edata['x'] = torch.ones(11, 2)
# 节点4的特征为[0.2, 0.5]
g.ndata['x'][4] = torch.tensor([0.2, 0.5])
# 边5的特征为[0.1, 0.1]
g.edata['x'][5] = torch.tensor([0.1, 0.1])
# 消息汇聚更新
# g.update_all(fn.copy_u(u='x', out='m'), fn.sum(msg='m', out='h'))
print(g.ndata['x'])
print(g.edata["x"])
消息传递
然后我们来试着理解一下消息传递:
def message_func(edges):
print("-"*20)
print("edges.data[x]", edges.data["x"]) # 获得边的特征
print("edges.src[x]", edges.src["x"]) # 获得边的源节点的特征
print("edges.dst[x]", edges.dst["x"]) # 获得边的目标节点的特征
# 返回得到需要传递的消息特征
return {'e_data': edges.data['x'], "e_src": edges.src["x"], "e_dst": edges.dst["x"]}
def reduce_func(nodes):
print("+"*20)
# 获取每个节点的边特征的和并储存在节点的e_data中
data_sum = th.sum(nodes.mailbox["e_data"], dim=1)
# 获取每条边的源节点特征并求和储存在节点的src_data中
src_sum = th.sum(nodes.mailbox["e_src"], dim=1)
# 获取每条边的目标节点特征并求和储存在节点的src_data中
dst_sum = th.sum(nodes.mailbox["e_dst"], dim=1)
print("nodes_e_data", data_sum)
print("nodes_e_src", src_sum)
print("nodes_e_dst", dst_sum)
return {"data_sum":data_sum, "src_sum":src_sum, "dst_sum":dst_sum}
def apply_node_func(nodes):
# 将x用data_sum更新
return {'x': nodes.data["data_sum"]}
g.update_all(message_func, reduce_func, apply_node_func)
print(g.ndata["x"])
我们就看一下用边特征更新后的x特征的输出好了。
g.ndata[“x”]的输出:
tensor([[1.0000, 1.0000],
[2.1000, 2.1000],
[2.0000, 2.0000],
[2.0000, 2.0000],
[3.0000, 3.0000]])
说明每个节点的入度的边的特征都求和之后汇聚到x特征上了,还是非常好理解的。
另外两个大概是求源节点相同的边的目标节点的特征的和来更新节点特征
以及求目标节点相同的边的源节点的特征的和来更新节点特征
可能说起来有点绕,但是看看代码运行的结果再结合图应该就懂了,这里就不放运行结果了。
这里是为了演示步骤,一般不再update_all中自己设置更新函数的。
graph.apply_edges
在DGL中,也可以在不涉及消息传递的情况下,通过 apply_edges() 单独调用逐边计算。 apply_edges() 的参数是一个消息函数。并且在默认情况下,这个接口将更新所有的边。
import dgl
import torch
g = dgl.graph(([0, 1, 2, 3], [1, 2, 3, 4]))
g.ndata['h'] = torch.ones(5, 2)
# 三种方式
# def add(edges):
# return{"x": edges.src['h'] + edges.dst['h']}
# g.apply_edges(add)
# g.apply_edges(lambda edges: {'x' : edges.src['h'] + edges.dst['h']}) # 二者等价
g.apply_edges(fn.u_add_v('h', 'h', 'x')) # 使用内置函数,是最好的
print(g.edata['x'])
算图的注意力机制的时候,可以先计算出每个边的注意力权重,此时直接边计算即可。
参考
https://docs.dgl.ai/guide_cn/message.html
https://docs.dgl.ai/guide_cn/message-api.html