基于MATLAB图像处理的硬币个数识别系统
基于MATLAB图像处理的硬币个数识别系统
1、课题介绍
本设计为基于MATLAB的硬币图像识别统计装置,通过数码相机获取平铺无重叠堆积的硬币的图像,并通过Matlab工具处理后统计硬币的数目。通过控制控制数码相机的拍摄实现拍摄—统计—拍摄的过程。在本次试验过程中,通过人为手动摆放硬币,在工业生产应用中可以由MCU实现硬币的传送,上位机实现统计显示。本装置的统计方式为软件识别,与传统的机械清点相比具有速度快,损耗低等特点,目前的缺陷就是清点精度相对比较的低。
2.总体方案设计
2.1 功能模块划分
在实验室实现的过程中检测传送装置可以省略,但考虑到该设计的实用性,再次针对工业生产进行模块设计。
该装置由检测传送控制、图像拍摄、软件处理三部分组成,MCU主要负责硬币的取送,数码相机负责图像的获取;而具体的任务分配及数据处理则由处理能力强大的上位机(PC机)来完成。
总体功能可由下图表示:
- 实验室手动操作:
图3-1-整体功能模块示意图
- 工业生产过程:
图3-1-2整体功能模块示意图
2.2 MCU传送控制流程
装置MCU控制传送的硬币及传送速度,这里主要介绍上位机图像处理部分,下位机的设计就不详细介绍。其与数码相机存在控制通讯接口,逻辑关系如下图所示:
2.3数码相机拍摄
数码相机获取的图片是后续程序处理的基础,所以在得到的图片质量上要有好的保证。比如图像的曝光度,解析度,对比度、色调等,所以有必要调整光照,设定好元件放置处的背景色。其中调整光照可以由MCU一并控制。数码相机的启停可由MCU控制,也可由PC控制,但图片所涉及的数据量大,要求失真度低,图像数据传输通讯接口可采用USB接口。这里使用imaging公司的摄像头和驱动进行上位机VC开发。
3.图像处理
3.1 图像格式转换
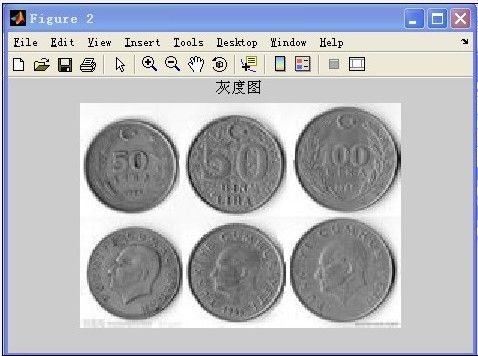
取的图像格式为RGB彩色图像,需要先将其转换为8位256级的灰度图像。本程序采用Matlab的图像处理工具箱的函数rgb2gray来实现。
rgb2gray()
功能:
转换RGB图像或颜色映像表为灰度图像。
语法:
I = rgb2gray(RGB)
newmap = rgb2gray(map)
3.2 去噪及特征提取
上图3-1为硬币统计的局部图片,图中可见,硬币主体部分和背景以及图像有着明显的区别,可以通过选取合适的阈值进行二值化,从而提取出硬币的特征。
图3-2为此图像的直方图,从图中可见到比较明显的阈值分界点,但是并不是非常的明显,这是因为,图中有很多的硬币因为反光的缘故,导致主体部分有些发白,如图3-3所示。
3.3灰度调整
对于这些发白部分,我们采用灰度调整及中值滤波进行处理,在matlab中,提供了两个函数进行相应的操作,其中imadjust进行灰度调整,其用法如下
Imadjst(f,[low_in high_in],[low_out high_out],gamma)
Gamma所表示的意义:
>1 -------- 凹曲线
<1 -------- 凸直线
=1 -------- 直线
medfilt2用于进行中值滤波处理,其用法如下
F=medfilt2(f,[m n]);
f为输入图像
[m n]为中值滤波模板
F是中值滤波后输出的图像。
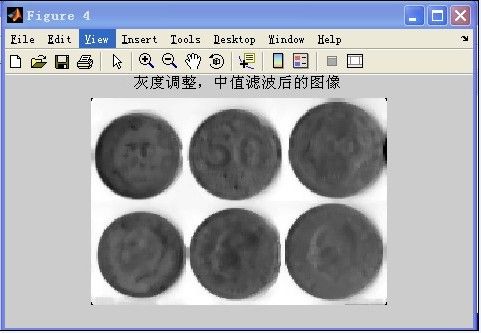
图4-1经过灰度调整及中值滤波后的图像如图4-4所示,可见,经过中值滤波后,硬币的主体部分有了较大的改善。
3.4二值化处理
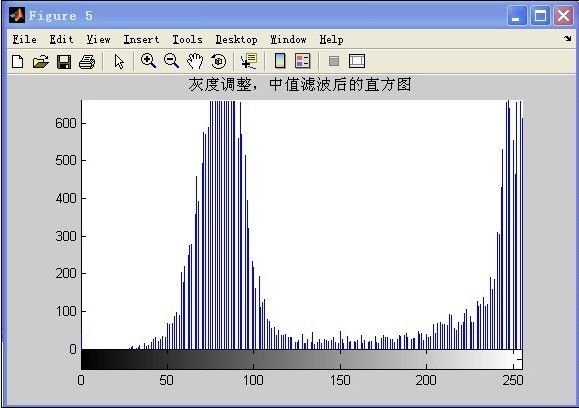
经过滤波后,即可对图像进行二值化处理,首先,我们采用人工选择阈值的方法进行二值化,由图可见,对于本幅图片,其合适的阈值在50~100之间,通过试验,我们选取的值为80。
对图像二值化处理的程序如下:
[M,N]=size(F);
for x=1:M
for y=1:N
if F(x,y)<80
F(x,y)=0; %低于阈值的值黑
else
F(x,y)=255; %高于阈值的值白
end
end
end
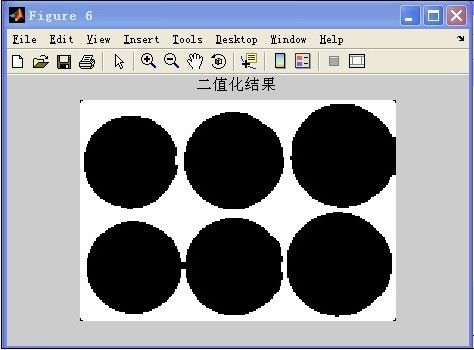
处理后的图像如图3-6所示:
3.5阈值分割
当然仍有许多模糊的硬币管脚残影,但已经将硬币的主体很好的识别了出来,采用人工选择阈值的方法虽然可以成功分离出硬币的主体,但是这个阈值这是针对这张图片有效,对于获取的其它图片,这个阈值并不能正确地对图像进行二值化处理,因此我们决定采用自动阈值分割的方法来对图像进行二值化。
我们所选用的自动阈值分割方法为Otsu法,它是一种使类间方差最大的自动确定阈值的方法,该方法具有简单、处理速度快的特点,是一种常用的阈值选取方法。
在matlab中,提供了一个函数graythresh来实现Otsu法阈值分割,其用法如下:
T=graythresh(f);
其中,f为待进行阈值分割的灰度图像,T为返回的分割灰度比例,将其乘于256即为Otsu法划定的分割阈值。
采用Otsu法进行阈值二值化后的图像如图4-7所示:
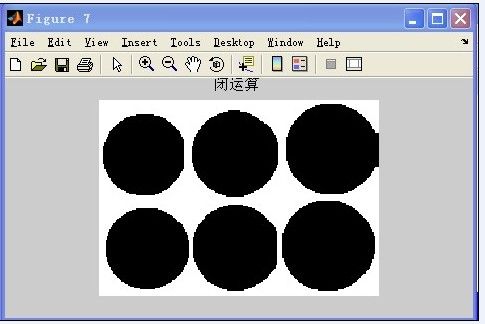
由上可见,不管是采用人工阈值还是Otsu法自动阈值分割,仍然会残留很多的硬币阴影,它们将会严重干扰到对硬币的统计,对于这些噪声,我们采用图像形态学中的闭运算来进行处理,闭运算的原理是先对图像进行腐蚀后再进行膨胀,matlab提供了函数imclose来实现图像的闭运算。其格式为:
F=imclose(f,B);
其中,B为结构元素,可由以下两种办法生成
(1) B=ones(n);
(2) B=strel(‘type’,[m n]);
Type可以取以下的值
square 生成一个m*n方形矩阵
line 生成一条长度为m,斜率为n°的直线
disk 生成一个m*n大小的蝶形
ball 生成一个m*n大小的球形
滤除硬币管脚后的结果如图4-8所示。
由图中可见,噪声被有效的滤除了,但是,去除了噪声的同时,也使部分接触紧密的硬币在闭运算后可能连成一个整体,如图4-8中的红圈所示,因此在此后的识别统计中需要对其进行特殊的处理。
4.识别统计
4.1图像反色
将以上处理过后的图像反色,如图4-10所示
图4-9 反色后的图像4.2函数bwlabel统计
硬币数目的统计采用函数bwlabel 来实现.
在该设计中由于6枚硬币已被人工有效的摆放,没有重叠部分,函数bwlabel的功能并没有有效的表现出来,但在大量测量硬币及细胞等物体计数时具有很广泛的应用。
bwlabel功能:
标注二进制图像中已连接的部分,并将每个连同的部分标上相同的序号。
语法: L = bwlabel(BW,n) ,[L,num] = bwlabel(BW,n)
统计的过程如下:
- 通过bwlabel计算出图像中所以的连通区域的数目,这包括了单个、两个、及三个以上的硬币。
- 计算每个连通区域的大小,根据大小判断其中包括的硬币数目,分别计算两个硬币,三个硬币,及三个以上硬币的数目。
- 将上面各项统计结果加起来即为硬币的数目。
具体程序如下:
%对图像贴标签
[L N]=bwlabel(F1,8)
Sum = [];
%统计每个标签的数量
for i=1:N
[r,c] = find(L==i);
rc = [r c];
Num = length(rc);
Sum([i])=Num;
end
%根据每个标签数量,分别统计2个,3个,4个硬币的数量
for i=1:length(Sum)
if (Sum([i]))>2000
N=N+3;
elseif (Sum([i])) > 900
N =N + 1;
end
end
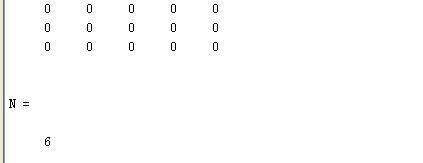
图4-10 Matlab统计分析
经过统计,如图4-10所示,该幅图像的硬币数目约为6个。
5.完整设计程序
clear all;
close all;
f=imread('H:\yingbi2.jpg');
w=imshow(f);title('原图像');
F=rgb2gray(f); %真彩图转化为灰度图
figure;imshow(F);title('灰度图');
figure;imhist(F);title('直方图');
F0 = imadjust(F,stretchlim(F),[0 1]);
Ft=medfilt2(F0,[5 5]);
figure;imshow(Ft);title('灰度调整,中值滤波后的图像');
figure;imhist(Ft);title('灰度调整,中值滤波后的直方图');
T=graythresh(Ft);
T=T*256-5;
[M,N]=size(Ft);
for x=1:M
for y=1:N
if Ft(x,y) Ft(x,y)=0; %低于阈值的值黑 else Ft(x,y)=255; %高于阈值的值白 end end end figure;imshow(Ft);title('二值化结果'); B=ones(10); F0=imclose(Ft,B); figure;imshow(F0);title('闭运算'); F1=imadjust(F0,[0,1],[1,0],1); figure;imshow(F1);title('反色'); %对图像贴标签 [L N]=bwlabel(F1,8) Sum = []; %统计每个标签的数量,有些硬币可能会重叠在一起的情况一定要用此种方法 %根据每个标签数量,硬币的数量 for i=1:length(Sum) if (Sum([i]))>2000 N=N+3; elseif(Sum([i])) > 1450 N =N + 2; elseif (Sum([i])) > 900 N =N + 1; end end