Python实现HOG+SVM

---

前言

由于近期接触到HOG+SVM行人识别检测这一方面，因此总结了一下关于HOG特征的一些基础知识。所引用的视频为sundog-education-hog，在此感谢投稿者。
更新！！！ 运用代码更加深刻认识HOG！！在此感谢大奥特曼打小怪兽。

---

一、梯度基础知识

• 对于函数$f(x,y)$,梯度是一个向量$(f_x,f_y)$
• 一张照片可看作是关于$(x,y)$的离散型函数，所以一张图片的梯度可以被计算出来。
• 对于每一个像素，图像的水平梯度和纵向梯度可以被计算出
• 这些向量有方向$atan(\frac{f_y}{f_x})$和大小$\sqrt{(f_x^2+f_y^2)}$
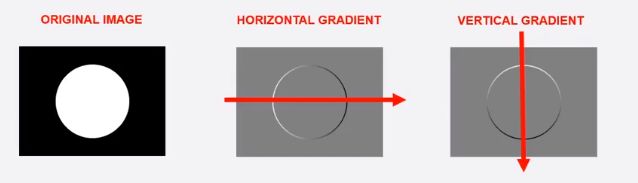
• 梯度值的范围为0-225，黑色为0，白色为225。像素从黑色急剧转为白色称为大的负向变化，颜色会变白色，像素如果仅有小的颜色变化或者没有变化会变为灰色
• 如水平梯度变化，很明显看出黑色-白色的部分变为白色，白色-黑色的部分变为黑色，其他部分为灰色

二、实例介绍

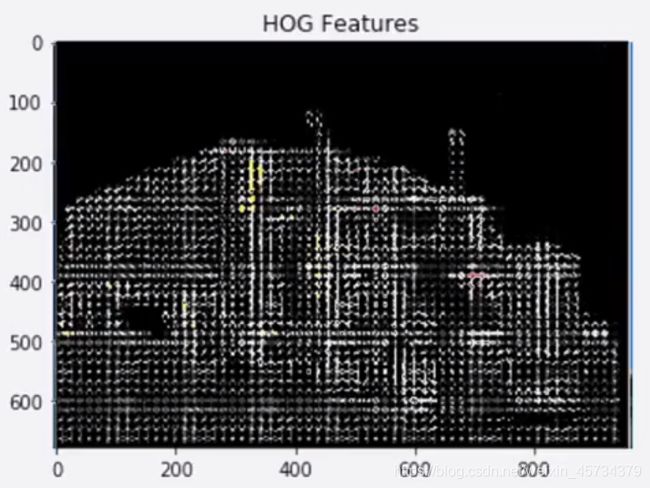
这里，我们来看一个实例，截取一个车子上的一块小的像素，它的像素值为上下左右分别为100，50，70，120：

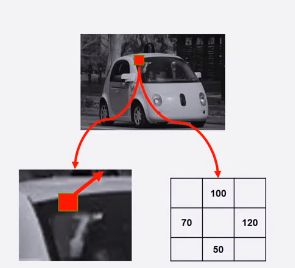
• X方向上的梯度值为120-70=50，Y方向上的梯度值为100-50=50，因此可以得到特征向量为$(50,50)$
• 因此特征向量的大小为$\sqrt{(50^2+50^2)}=70.1$，特征向量的方向为$ta{n}^{-1}(50/50)=45^{\circ }$，正如上图左下图的箭头大小和指向

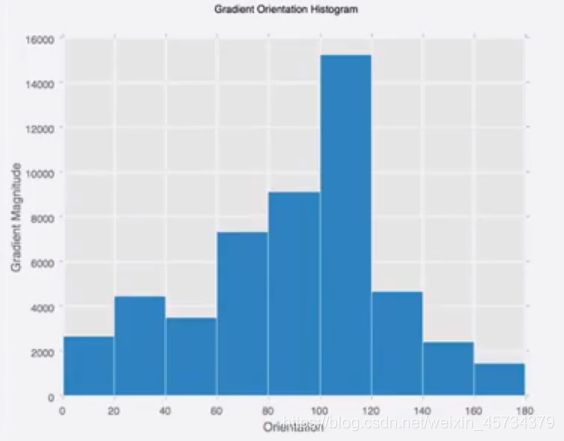
三、计算直方图步骤

-我们以大卡车为例， 用一个cell(8x8)来计算梯度的大小和方向,总共有64的特征向量的大小和方向

• 创建一个直方图关于这64个特征向量，如下面的方向梯度直方图所示，每个特征向量可以被放入这9个柱形中的其中一个，这样我们就将64的向量变换为9个值
  

四、总结

• HOG是一种特征描述可以运用在目标检测上
• HOG加上SVM分类器可以work well 在目标检测上
• HOG运用一种滑窗技术在一张图片上，并且HOG 特征描述是针对于每一固定位置（滑窗大小）来产生的
  

五、Python实际操作

• Python运行平台：Jupyter Notebook
• 所运用的照片只有197_1_t20201119084916148_CAM1_18.jpg，可以随意替换
• 该图片像素为1333*1333，绿色框里表示一个白色瑕疵点，想查看白色瑕疵周围的HOG描述
  

import cv2
import numpy as np
import math
import matplotlib.pyplot as plt


class Hog_descriptor():
    '''
    HOG描述符的实现
    '''
    def __init__(self, img, cell_size=8, bin_size=9):
        '''
        构造函数
            默认参数，一个block由2x2个cell组成，步长为1个cell大小 
        args:
            img：输入图像(更准确的说是检测窗口)，这里要求为灰度图像  对于行人检测图像大小一般为128x64 即是输入图像上的一小块裁切区域
            cell_size：细胞单元的大小 如8，表示8x8个像素
            bin_size：直方图的bin个数
        '''
        self.img = img
        '''
        采用Gamma校正法对输入图像进行颜色空间的标准化（归一化），目的是调节图像的对比度，降低图像局部
        的阴影和光照变化所造成的影响，同时可以抑制噪音。采用的gamma值为0.5。 f(I)=I^γ
        '''
        self.img = np.sqrt(img*1.0 / float(np.max(img)))
        self.img = self.img * 255
        #print('img',self.img.dtype)   #float64
        #参数初始化
        self.cell_size = cell_size
        self.bin_size = bin_size
        self.angle_unit = 180 / self.bin_size  #这里采用180°
        assert type(self.bin_size) == int, "bin_size should be integer,"
        assert type(self.cell_size) == int, "cell_size should be integer,"
        assert 180 % self.bin_size == 0, "bin_size should be divisible by 180"

    def extract(self):
        '''
        计算图像的HOG描述符，以及HOG-image特征图
        '''
        height, width = self.img.shape
        '''
        1、计算图像每一个像素点的梯度幅值和角度
        '''
        gradient_magnitude, gradient_angle = self.global_gradient()
        gradient_magnitude = abs(gradient_magnitude)
        '''
        2、计算输入图像的每个cell单元的梯度直方图，形成每个cell的descriptor 比如输入图像为128x64 可以得到16x8个cell，每个cell由9个bin组成
        '''
        cell_gradient_vector = np.zeros((int(height / self.cell_size), int(width / self.cell_size), self.bin_size))
        #遍历每一行、每一列
        for i in range(cell_gradient_vector.shape[0]):
            for j in range(cell_gradient_vector.shape[1]):
                #计算第[i][j]个cell的特征向量
                cell_magnitude = gradient_magnitude[i * self.cell_size:(i + 1) * self.cell_size,
                                 j * self.cell_size:(j + 1) * self.cell_size]
                cell_angle = gradient_angle[i * self.cell_size:(i + 1) * self.cell_size,
                             j * self.cell_size:(j + 1) * self.cell_size]
                cell_gradient_vector[i][j] = self.cell_gradient(cell_magnitude, cell_angle)

        #将得到的每个cell的梯度方向直方图绘出，得到特征图
        hog_image = self.render_gradient(np.zeros([height, width]), cell_gradient_vector)
        
        '''
        3、将2x2个cell组成一个block，一个block内所有cell的特征串联起来得到该block的HOG特征descriptor
           将图像image内所有block的HOG特征descriptor串联起来得到该image（检测目标）的HOG特征descriptor，
           这就是最终分类的特征向量
        '''
        hog_vector = []
        #默认步长为一个cell大小，一个block由2x2个cell组成，遍历每一个block
        for i in range(cell_gradient_vector.shape[0] - 1):
            for j in range(cell_gradient_vector.shape[1] - 1):
                #提取第[i][j]个block的特征向量
                block_vector = []
                block_vector.extend(cell_gradient_vector[i][j])
                block_vector.extend(cell_gradient_vector[i][j + 1])
                block_vector.extend(cell_gradient_vector[i + 1][j])
                block_vector.extend(cell_gradient_vector[i + 1][j + 1])
                '''块内归一化梯度直方图，去除光照、阴影等变化，增加鲁棒性'''
                #计算l2范数
                mag = lambda vector: math.sqrt(sum(i ** 2 for i in vector))   
                magnitude = mag(block_vector) + 1e-5
                #归一化
                if magnitude != 0:
                    normalize = lambda block_vector, magnitude: [element / magnitude for element in block_vector]
                    block_vector = normalize(block_vector, magnitude)
                hog_vector.append(block_vector)           
        return np.asarray(hog_vector), hog_image

    def global_gradient(self):
        '''
        分别计算图像沿x轴和y轴的梯度
        '''
        gradient_values_x = cv2.Sobel(self.img, cv2.CV_64F, 1, 0, ksize=5)
        gradient_values_y = cv2.Sobel(self.img, cv2.CV_64F, 0, 1, ksize=5)
        #计算梯度幅值 这个计算的是0.5*gradient_values_x + 0.5*gradient_values_y
        #gradient_magnitude = cv2.addWeighted(gradient_values_x, 0.5, gradient_values_y, 0.5, 0)
        #计算梯度方向
        #gradient_angle = cv2.phase(gradient_values_x, gradient_values_y, angleInDegrees=True)
        gradient_magnitude, gradient_angle = cv2.cartToPolar(gradient_values_x,gradient_values_y,angleInDegrees=True)        
        #角度大于180°的，减去180度
        gradient_angle[gradient_angle>180.0] -= 180 
        #print('gradient',gradient_magnitude.shape,gradient_angle.shape,np.min(gradient_angle),np.max(gradient_angle))
        return gradient_magnitude, gradient_angle

    def cell_gradient(self, cell_magnitude, cell_angle):
        '''
        为每个细胞单元构建梯度方向直方图
        
        args:
            cell_magnitude：cell中每个像素点的梯度幅值
            cell_angle：cell中每个像素点的梯度方向
        return：
            返回该cell对应的梯度直方图，长度为bin_size
        '''
        orientation_centers = [0] * self.bin_size
        #遍历cell中的每一个像素点
        for i in range(cell_magnitude.shape[0]):
            for j in range(cell_magnitude.shape[1]):
                #梯度幅值
                gradient_strength = cell_magnitude[i][j]
                #梯度方向
                gradient_angle = cell_angle[i][j]
                #双线性插值
                min_angle, max_angle, weight = self.get_closest_bins(gradient_angle)
                orientation_centers[min_angle] += (gradient_strength * (1 - weight))
                orientation_centers[max_angle] += (gradient_strength *weight)
        return orientation_centers

    def get_closest_bins(self, gradient_angle):
        '''
        计算梯度方向gradient_angle位于哪一个bin中，这里采用的计算方式为双线性插值
        具体参考：https://www.leiphone.com/news/201708/ZKsGd2JRKr766wEd.html
        例如：当我们把180°划分为9个bin的时候，分别对应对应0,20,40,...160这些角度。
              角度是10，副值是4，因为角度10介于0-20度的中间(正好一半)，所以把幅值
              一分为二地放到0和20两个bin里面去。
        args:
            gradient_angle:角度
        return：
            start,end,weight：起始bin索引，终止bin的索引，end索引对应bin所占权重
        '''
        idx = int(gradient_angle / self.angle_unit)
        mod = gradient_angle % self.angle_unit
        return idx % self.bin_size, (idx + 1) % self.bin_size, mod / self.angle_unit

    def render_gradient(self, image, cell_gradient):
        '''
        将得到的每个cell的梯度方向直方图绘出，得到特征图
        args：
            image：画布,和输入图像一样大 [h,w]
            cell_gradient：输入图像的每个cell单元的梯度直方图,形状为[h/cell_size,w/cell_size,bin_size]
        return：
            image：特征图
        '''
        cell_width = self.cell_size / 2
        max_mag = np.array(cell_gradient).max()
        #遍历每一个cell
        for x in range(cell_gradient.shape[0]):
            for y in range(cell_gradient.shape[1]):
                #获取第[i][j]个cell的梯度直方图
                cell_grad = cell_gradient[x][y]
                #归一化
                cell_grad /= max_mag
                angle = 0
                angle_gap = self.angle_unit
                #遍历每一个bin区间
                for magnitude in cell_grad:
                    #转换为弧度
                    angle_radian = math.radians(angle)
                    #计算起始坐标和终点坐标，长度为幅值(归一化),幅值越大、绘制的线条越长、越亮
                    x1 = int(x * self.cell_size + cell_width + magnitude * cell_width * math.cos(angle_radian))
                    y1 = int(y * self.cell_size + cell_width + magnitude * cell_width * math.sin(angle_radian))
                    x2 = int(x * self.cell_size + cell_width - magnitude * cell_width * math.cos(angle_radian))
                    y2 = int(y * self.cell_size + cell_width - magnitude * cell_width * math.sin(angle_radian))
                    cv2.line(image, (y1, x1), (y2, x2), int(255 * math.sqrt(magnitude)))
                    angle += angle_gap
        return image

        
if __name__ == '__main__':
    #加载图像
    img = cv2.imread('F:/TTTianchi/Onepicture/segment/197_1_t20201119084916148_CAM1_18.jpg')        
    width = 133
    height = 133 #有更改
    img_copy = img[800:800+height,100:100+width][:,:,::-1]    #看看白色瑕疵点大致位置
    gray_copy = cv2.cvtColor(img_copy,cv2.COLOR_BGR2GRAY)
    
    #显示原图像
    plt.figure(figsize=(10,10))
    plt.subplot(1,2,1)
    plt.imshow(img_copy)
    
    #HOG特征提取
    hog = Hog_descriptor(gray_copy, cell_size=5, bin_size=9)  
    hog_vector, hog_image = hog.extract()
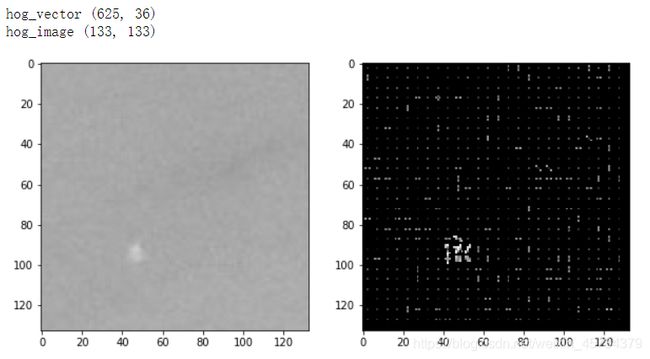
    print('hog_vector',hog_vector.shape)
    print('hog_image',hog_image.shape)
    
    #绘制特征图
    plt.subplot(1,2,2)
    plt.imshow(hog_image, cmap=plt.cm.gray)    
    plt.show()

• 结果显示 白色瑕疵点的结构很容易在HOG图中看出——一团明显的白色

• 我们来计算加深对于HOG的印象
• 对于133x133的窗口，cell的大小为8x8，9个bin大小的直方图，block为2x2的cell，以1个cell为步长
• 水平、垂直方向有133/5-1=25.6，即25个扫描窗口，所以hog_vector为(25x25,2x2x9)
• 一共有25x25x2x2x9=22500个HOG特征