详细介绍遗传算法的原理以及最值问题代码实现(MATLAB/Python)
文章目录
- 一、智能优化算法和传统算法的对比
- 二、遗传算法
-
- 1、由来
- 2、基本思想
- 3、以传统算法相比,遗传算法的优势
- 4、基本概念
- 5、三大操作
- 6、基本步骤
- 7、应用举例
- 8、代码实现
-
- (1)单变量最值问题
-
- MALBAN代码
- python代码
- (2)双变量最值问题
-
- MATLAB代码
- python代码
一、智能优化算法和传统算法的对比
传统的优化方法
1)依赖于初始条件。
2)与求解空间有紧密关系,促使较快地收敛到局部解,但同时对解域有约束,如可微或连续。利用这些约束,收敛快。
3)有些方法,如Davison-Fletcher-Powell直接依赖于至少一阶导数;共轭梯度法隐含地依赖于梯度。
智能优化方法
1)不依赖于初始条件;
2)不与求解空间有紧密关系,对解域,无可微或连续的要求。求解稳健,但收敛速度慢。能获得全局最优。适合于求解空间不知的情况。
二、遗传算法
1、由来
遗传算法(Genetic Algorithm,简称 GA),是模拟达尔文的遗传选择和自然淘汰的生物进化过程以及Mendel遗传学的计算机算法。它由美国Holland教授1975年提出。
2、基本思想
遗传算法是基于模仿生物界遗传学的遗传过程,把问题的参数用基因来表示,把问题的解用染色体来表示代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体。这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代,后代随机化地继承父代的最好特征,并也在生存环境的控制支配下继续这一过程。群体的染色体都将逐渐适应环境,不断进化,最后收敛到一组最适应环境的类似个体,即得到问题最优解。
3、以传统算法相比,遗传算法的优势
与传统的优化算法相比,遗传算法主要有以下几个不同之处:
①遗传算法不是直接作用在参变量集上而是利用参变量集的某种编码;
②遗传算法不是从单个点,而是从一个点的群体开始搜索;
③遗传算法利用适应值信息,无须导数或其它辅助信息;
④遗传算法利用概率转移规则,而非确定性规则;
⑤它在搜索过程中不容易陷入局部最优,即使所定义的适应函数是不连续的、非规则的或有噪声的情况下,它也能以很大的概率找到整体最优解;
⑥由于它固有的并行性,遗传算法非常适用于大规模并行计算机。
4、基本概念
(1)个体与种群
个体就是模拟生物个体而对问题中的对象(一般就是问题的解)的一种称呼,一个
个体也就是搜索空间中的一个点。
种群(population)就是模拟生物种群而由若干个体组成的群体,它一般是整个搜索空间的
一个很小的子集。
(2)适应度与适应度函数
适应度(fitness)就是借鉴生物个体对环境的适应程度,而对问题中的个体对象所设计的表征其优劣的一种测度。
适应度函数(fitness function)就是问题中的全体个体与其适应度之间的一个对应关系。它一般是一个实值函数。该函数就是遗传算法中评价个体优劣的评价函数。
适应度函数的重要性
适应度函数的选取直接影响遗传算法的收敛速度以及能否找到最优解。一般而言,适应度函数是由目标函数变换而成的,对目标函数值域的某种映射变换称为适应度的尺度变换(fitness scaling)。
适应度函数的设计
- 单值、连续、非负、最大化
- 合理、一致性
- 计算量小
- 通用性强
常见的适应度函数
若目标函数为最大化问题:Fit(f(x))=f(x)
若目标函数为最小化问题:Fit(f(x))=-f(x)
(3)染色体和基因
染色体(chromosome)就是问题中个体的某种字符串形式的编码表示。字符串中的字符也就称为基因(gene)。

(4)编码和解码
二进制编码方法是遗传算法中最常用的一种编码方法,它使用的编码符号集是由二进制符号0和1所组成的二值符号集{0,1},它所构成的个体基因型是一个二进制编码符号串。



二进制编码方法的优点:
①编码、解码操作简单易行;
②交叉、变异等遗传操作便于实现;
③符合最小字符集编码原则(使用能使问题得到自然表示或描述的具
有最小编码字符集的编码方案。);
④便于利用模式定理对算法进行理论分析。


5、三大操作
亦称遗传算子(genetic operator),就是关于染色体的运算。遗传算法中有三种遗传操作:
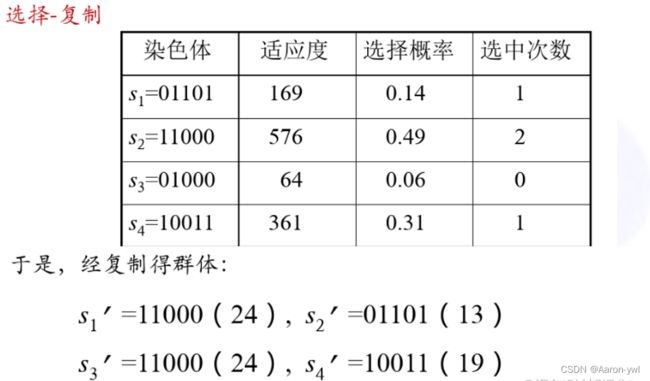
① 选择-复制(selection-reproduction)
②交叉(crossover,亦称交换、交配或杂交)
③变异(mutation,亦称突变)







6、基本步骤
①选择编码策略,把参数集合(可行解集合)转换染色体结构空间;
②定义适应度函数,便于计算适应值;
③确定遗传策略,包括选择群体大小,选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数;
④随机产生初始化群体;
⑤计算群体中的个体或染色体解码后的适应值;
⑥按照遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代群体;
⑦判断群体性能是否满足某一指标,或者已完成预定的迭代次数,不满足则返回第五步,或者修改遗传策略再返回第六步。
步骤概述
(1)把问题的解表示成“染色体”。在算法中就是以二进制编码的串,给出一群“染色体”,也就是假设的可行解;
(2)把这些可行解置于问题的“环境”中,按适者生存的原则,选取较适应环境的“染色体”进行复制,并通过交叉、变异过程产生更适应环境的新一代“染色体”群;
(3)经过这样的一代一代地进化,最后就会收敛到最适应环境的一个“染色体”上,它就是问题的最优解。

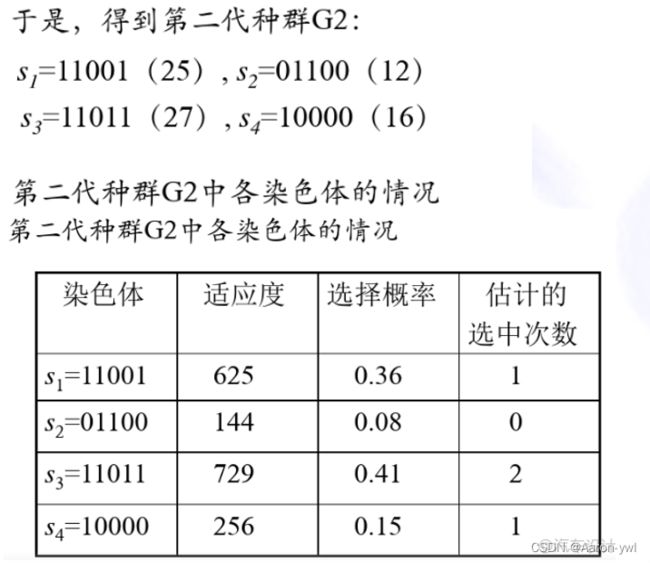
7、应用举例
8、代码实现
(1)单变量最值问题
求解函数y=sin(x)+pi*cos(x)-exp(x.^2+3),x∈[-1,1] 的最大值
MALBAN代码
视频地址:通俗易懂讲算法-最优化之遗传算法(GA)
计算适应度
% 计算适应度
function fitvalue = calfitvalue(fx)
%这里求最大值,并且函数值又都大于0,所以直接使用函数值本身作为适应度值。
% 事实上,不同的问题适应度函数构造方法多种多样。
fitvalue = fx ;
end
复制操作
% 复制操作
function newx = copyx(pop, fitvalue,popsize ) %传进来二进制串和对应适应度
% 按照PPT的轮盘赌策略对个体复制
newx = pop; %只是起到申请一个size为pop大小空间的作用,newx之后要更新的
i = 1; j = 1;
p = fitvalue / sum(fitvalue) ;
Cs = cumsum(p) ;
R = sort(rand(popsize,1)) ; %每个个体的复制概率
while j <= popsize
if R(j) < Cs(i)
newx(j,:) = pop(i,:) ;
j = j + 1;
else
i = i + 1;
end
end
end
交叉操作
% 交叉操作
function newx = crossover(pop, pc, popsize,chromlength )
% 12 34 56交叉方式,随机选择交叉位点
% 注意个体数为奇数偶数的区别
i = 2 ;
newx = pop ; %申请空间
while i + 2 <= popsize
%将第i 与 第 i -1 进行随机位点交叉
if rand < pc
x1 = pop(i-1,:);
x2 = pop(i,:) ;
r = randperm( chromlength , 2 ) ; %返回范围内两个整数
r1 = min(r); r2 =max(r) ; % 交叉复制的位点
newx(i-1,:) = [x1( 1 : r1-1),x2(r1:r2) , x1(r2+1: end)];
newx(i , : ) = [x2( 1 : r1-1),x1(r1:r2) , x2(r2+1: end)];
end
i = i + 2 ; %更新i
end
end
变异操作
% 变异操作
function newx = mutation(pop,pm, popsize,chromlength)
i = 1 ;
while i <= popsize
if rand < pm
r = randperm( chromlength , 1 ) ;
pop(i , r) = ~pop(i, r);
end
i = i + 1;
end
newx = pop; %将变异后的结果返回。
end
解码,二进制转十进制操作
% 二进制转十进制函数
function dec = bintodec( pop ,popsize, chromlength,xlim )
dec = zeros(1,chromlength);
index = chromlength-1:-1:0;
for i = 1 : popsize
dec(i) = sum(pop(i,:).* (2.^index));
end
dec = xlim(1) + dec*( xlim(2) - xlim(1) ) /( 2 ^ chromlength - 1) ;
end
绘制图像
% 绘制图像
function plotfig(decpop , fx ,xlim,k)
f = @(x) sin(x)+pi*cos(x)-exp(x.^2+3); % 研究对象函数
x = xlim(1):0.05:xlim(2);
y = f(x) ;
subplot(1,2,1);
plot(x,y,decpop,fx,'o')
title(['第',num2str(k),'次迭代进化'])
pause(0.2)
end
目标函数
% 目标函数
function fx = calobjvalue(decpop ) %参数为十进制解
f = @(x) sin(x)+pi*cos(x)-exp(x.^2+3); % 研究对象函数
fx = f(decpop);
end
主程序
%主程序
function GA()
clear
close all
popsize=50; % 群体大小
chromlength=20; %字符串的长度(个体长度)
pc=0.95; %交叉概率
pm=0.01; %变异概率
xlim = [-1,1]; %自变量范围
G = 100 ; %迭代次数
pop= round( rand(popsize,chromlength) ) ; %随机产生初始群体
decpop = bintodec( pop ,popsize, chromlength,xlim ) ; % 计算初代解对应十进制
fx = calobjvalue(decpop ) ; % 计算初代解的函数值
plotfig(decpop , fx , xlim , 1 ) ; % 绘制图像
[y(1) , l ] = min(fx); x(1) = decpop(l);
for i=2 : G
decpop = bintodec( pop , popsize, chromlength,xlim ) ; % 计算上一代解对应十进制
fx = calobjvalue(decpop ) ; % 计算上一代解的函数值
fitvalue = calfitvalue(fx) ; % 适应度映射
newpop = copyx(pop,fitvalue,popsize); %复制
newpop = crossover(newpop, pc, popsize,chromlength ); %交叉
newpop = mutation(newpop,pm, popsize,chromlength); %变异
% 这时的newpop是经过复制交叉变异产生的新一代群体
% 下边进行选择择优保留(即实现保底机制)
newdecpop = bintodec( newpop ,popsize, chromlength,xlim ) ;
new_fx = calobjvalue(newdecpop) ; %计算新解目标函数
new_fitvalue = calfitvalue(new_fx); %计算新群体中每个个体的适应度
index = find(new_fitvalue > fitvalue) ;
pop(index, : ) = newpop(index,:) ; % 更新得到最新解
decpop = bintodec( pop ,popsize, chromlength,xlim ) ; %计算新解的十进制
fx = calobjvalue( decpop ) ; %计算结果
plotfig(decpop , fx ,xlim , i ) % 绘制新解的图
% 找出更新后的个体最优函数值
[bestindividual,bestindex] = max( fx ) ;
y(i)=bestindividual; % 记录每一代的最优函数值
x(i)= decpop(bestindex) ; %十进制解
subplot(1,2,2);
plot(1:i,y);
title('适应度进化曲线');
i = i + 1 ;
end
[ymax, max_index] = max(y);
disp(['找的最优解位置为:', num2str(x(max_index)) ])
disp(['对应最优解为:', num2str(ymax) ])
end
完整代码
%主程序
function GA()
clear
close all
popsize=50; % 群体大小
chromlength=20; %字符串的长度(个体长度)
pc=0.95; %交叉概率
pm=0.01; %变异概率
xlim = [-1,1]; %自变量范围
G = 100 ; %迭代次数
pop= round( rand(popsize,chromlength) ) ; %随机产生初始群体
decpop = bintodec( pop ,popsize, chromlength,xlim ) ; % 计算初代解对应十进制
fx = calobjvalue(decpop ) ; % 计算初代解的函数值
plotfig(decpop , fx , xlim , 1 ) ; % 绘制图像
[y(1) , l ] = min(fx); x(1) = decpop(l);
for i=2 : G
decpop = bintodec( pop , popsize, chromlength,xlim ) ; % 计算上一代解对应十进制
fx = calobjvalue(decpop ) ; % 计算上一代解的函数值
fitvalue = calfitvalue(fx) ; % 适应度映射
newpop = copyx(pop,fitvalue,popsize); %复制
newpop = crossover(newpop, pc, popsize,chromlength ); %交叉
newpop = mutation(newpop,pm, popsize,chromlength); %变异
% 这时的newpop是经过复制交叉变异产生的新一代群体
% 下边进行选择择优保留(即实现保底机制)
newdecpop = bintodec( newpop ,popsize, chromlength,xlim ) ;
new_fx = calobjvalue(newdecpop) ; %计算新解目标函数
new_fitvalue = calfitvalue(new_fx); %计算新群体中每个个体的适应度
index = find(new_fitvalue > fitvalue) ;
pop(index, : ) = newpop(index,:) ; % 更新得到最新解
decpop = bintodec( pop ,popsize, chromlength,xlim ) ; %计算新解的十进制
fx = calobjvalue( decpop ) ; %计算结果
plotfig(decpop , fx ,xlim , i ) % 绘制新解的图
% 找出更新后的个体最优函数值
[bestindividual,bestindex] = max( fx ) ;
y(i)=bestindividual; % 记录每一代的最优函数值
x(i)= decpop(bestindex) ; %十进制解
subplot(1,2,2);
plot(1:i,y);
title('适应度进化曲线');
i = i + 1 ;
end
[ymax, max_index] = max(y);
disp(['找的最优解位置为:', num2str(x(max_index)) ])
disp(['对应最优解为:', num2str(ymax) ])
end
% 计算适应度
function fitvalue = calfitvalue(fx)
%这里求最大值,并且函数值又都大于0,所以直接使用函数值本身作为适应度值。
% 事实上,不同的问题适应度函数构造方法多种多样。
fitvalue = fx ;
end
% 复制操作
function newx = copyx(pop, fitvalue,popsize ) %传进来二进制串和对应适应度
% 按照PPT的轮盘赌策略对个体复制
newx = pop; %只是起到申请一个size为pop大小空间的作用,newx之后要更新的
i = 1; j = 1;
p = fitvalue / sum(fitvalue) ;
Cs = cumsum(p) ;
R = sort(rand(popsize,1)) ; %每个个体的复制概率
while j <= popsize
if R(j) < Cs(i)
newx(j,:) = pop(i,:) ;
j = j + 1;
else
i = i + 1;
end
end
end
% 交叉操作
function newx = crossover(pop, pc, popsize,chromlength )
% 12 34 56交叉方式,随机选择交叉位点
% 注意个体数为奇数偶数的区别
i = 2 ;
newx = pop ; %申请空间
while i + 2 <= popsize
%将第i 与 第 i -1 进行随机位点交叉
if rand < pc
x1 = pop(i-1,:);
x2 = pop(i,:) ;
r = randperm( chromlength , 2 ) ; %返回范围内两个整数
r1 = min(r); r2 =max(r) ; % 交叉复制的位点
newx(i-1,:) = [x1( 1 : r1-1),x2(r1:r2) , x1(r2+1: end)];
newx(i , : ) = [x2( 1 : r1-1),x1(r1:r2) , x2(r2+1: end)];
end
i = i + 2 ; %更新i
end
end
% 变异操作
function newx = mutation(pop,pm, popsize,chromlength)
i = 1 ;
while i <= popsize
if rand < pm
r = randperm( chromlength , 1 ) ;
pop(i , r) = ~pop(i, r);
end
i = i + 1;
end
newx = pop; %将变异后的结果返回。
end
% 二进制转十进制函数
function dec = bintodec( pop ,popsize, chromlength,xlim )
dec = zeros(1,chromlength);
index = chromlength-1:-1:0;
for i = 1 : popsize
dec(i) = sum(pop(i,:).* (2.^index));
end
dec = xlim(1) + dec*( xlim(2) - xlim(1) ) /( 2 ^ chromlength - 1) ;
end
% 绘制图像
function plotfig(decpop , fx ,xlim,k)
f = @(x) sin(x)+pi*cos(x)-exp(x.^2+3); % 研究对象函数
x = xlim(1):0.05:xlim(2);
y = f(x) ;
subplot(1,2,1);
plot(x,y,decpop,fx,'o')
title(['第',num2str(k),'次迭代进化'])
pause(0.2)
end
% 目标函数
function fx = calobjvalue(decpop ) %参数为十进制解
f = @(x) sin(x)+pi*cos(x)-exp(x.^2+3); % 研究对象函数
fx = f(decpop);
end
效果展示
找的最优解位置为:0.02307
对应最优解为:-16.9324
如果想要计算最小值,直接把计算适应度函数的
fx成-fx即可:
例如将fitvalue = fx ;改成fitvalue = -fx ;
还要将[ymax, max_index] = max(y);改成[ymax, max_index] = min(y);
python代码
完整代码
# 遗传算法
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# %matplotlib auto
DNA_SIZE=20 # DNA长度
POP_SIZE=100 # 种群大小
CROSSVER_RATE=0.95 # 交叉概率
MUTATION_RATE=0.5 # 变异概率
N_GENERATIONS=20 # 迭代次数
X_BOUND=[-1,1] # x的取值范围
# 目标函数
def F(x):
return np.sin(x)+np.pi*np.cos(x)-np.exp(x**2+3)
# 绘制2d图像
def plot_2d(ax):
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X = np.linspace(*X_BOUND,100)
line, = ax.plot(X, F(X))
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.pause(0.5)
plt.show()
# 计算适应值
def get_fitness(pop):
x=translateDNA(pop)
pred=F(x)
return (pred-np.min(pred))+1e-3
'''
减去最小的适应度是为了防止适应度出现负数,
通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],
最后在加上一个很小的数防止出现为0的适应度
'''
# 解码过程
# pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
def translateDNA(pop):
'''
解码
:param pop: 种群矩阵,一行表示一个二进制编码的个体(可能解),行数为种群中个体数目
:return: 返回的x是一个行为种群大小 列为1的矩阵
'''
x_pop=pop[:,1::2] # pop中的奇数列表示x
x=x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]
return x
# 交叉操作
def crossover_and_mutation(pop,CROSSVER_RATE):
new_pop=[]
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child=father # 孩子先得到父亲的全部基因(代表一个个体的一个二进制0,1串)
if np.random.rand() <CROSSVER_RATE: #产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother=pop[np.random.randint(POP_SIZE)] # 在种群中选择另一个个体作为母亲
cross_points=np.random.randint(low=0,high=DNA_SIZE*2) #随机产生交叉的点
child[cross_points:]=mother[cross_points:]
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
# 变异操作
def mutation(child,MUTATION_RATE):
if np.random.rand()<MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_points=np.random.randint(0,DNA_SIZE*2) # 随机产生一个实数,代表要变异基因的位置
child[mutate_points]=child[mutate_points]^1 # 将变异点位置的二进制反转
# 选择适应值高的个体
def select(pop,fitness): # 自然选择,优胜劣汰
idx=np.random.choice(np.arange(POP_SIZE),size=POP_SIZE,replace=True,p=(fitness)/fitness.sum())
return pop[idx]
# 计算结果
def print_info(pop):
fitness=get_fitness(pop)
max_fitness_index=np.argmax(fitness)
x=translateDNA(pop)
# print('最优基因型:',pop[max_fitness_index])
print('x:',x[max_fitness_index])
print('函数最大值:%s'%(F(x[max_fitness_index])))
if __name__=='__main__':
fig, ax = plt.subplots()
plt.ion() # 将画图模式改为交互模式,程序遇到plt.show不会暂停,而是继续执行
plot_2d(ax)
pop=np.random.randint(2,size=(POP_SIZE,DNA_SIZE*2)) # matrix (POP_SIZE, DNA_SIZE)
for i in range(N_GENERATIONS): # 迭代N代
x=translateDNA(pop)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x,F(x), c='black', marker='o')
ax.set_title(f'迭代第{i+1}次,一共要迭代{N_GENERATIONS}次')
plt.show()
plt.pause(0.5)
fitness=get_fitness(pop) # 得到适应度
pop=select(pop,fitness) # 优胜劣汰,选择生成新的种群
print_info(pop) # 计算结果
# 显示前关掉交互模式
# 在plt.show()之前一定不要忘了加plt.ioff(),如果不加,界面会一闪而过,并不会停留。
plt.ioff()
plot_2d(ax)
结果展示

x: 0.0313425362992632
函数最大值:-16.933890631152764
当求解变量最小值的问题时,把计算适应值函数改成如下结果即可:
def get_fitness(pop):
x,y = translateDNA(pop)
pred = F(x, y)
return np.max(pred) - pred + 1e-3
(2)双变量最值问题
求解函数y=3x1-2x2,x∈[-1,2] 的最大值
MATLAB代码
完整代码
clc;
clear all;
format long; %设定数据显示格式
%初始化参数
T=10; %迭代代数
N=50; %群体规模
pm=0.01; % 变异概率
pc=0.95; % 交叉概率
umax=2;
umin=-1; %参数取值范围
L=3; %单个参数字串长度,总编码长度2L
bval=round(rand(N,2*L)); %初始种群
bestv=-inf; %最优适应度初值
%迭代开始
for ii=1:T
%解码,计算适应度
for i=1:N
y1=0;y2=0;
for j=1:L
y1=y1+bval(i,L-j+1)*2^(j-1);
end
x1=(umax-umin)*y1/(2^L-1)+umin;
for j=1:L
y2=y2+bval(i,2*L-j+1)*2^(j-1);
end
x2=(umax-umin)*y2/(2^L-1)+umin;
obj(i)=3*x1-2*x2; %目标函数
xx(i,:)=[x1,x2];
end
func=obj; %目标函数转换为适应度函数
p=func./sum(func);
q=cumsum(p); % 累加
[fmax,indmax]=max(func); %求当代最佳个体
if fmax>=bestv
bestv=fmax; %到目前为止最优适应度值
bvalxx=bval(indmax,:); %到目前为止最佳位串
optxx=xx(indmax,:);% 到目前为止最优参数
end
Bfit1(ii)=bestv; %存储每代的最优适应度
%遗传操作开始
%轮盘赌选择
for i=1:(N-1)
r=rand;
tmp=find(r<=q);
newbval(i,:)=bval(tmp(1),:);
end
newbval(N,:)=bvalxx; %最优保留
bval=newbval;
%单点交叉
for i=1:2:(N-1)
cc=rand;
if cc<pc
point=ceil(rand*(2*L-1)); %取得一个1到2L-1的整数
ch=bval(i,:);
bval(i,point+1:2*L)=bval(i+1,point+1:2*L);
bval(i+1,point+1:2*L)=ch(1,point+1:2*L);
end
end
bval(N,:)=bvalxx; %最优保留
%位点变异
mm=rand(N,2*L)<pm; %小于变异概率赋值为1,其它复制为0
mm(N,:)=zeros(1,2*L); %最后一行不变异,强制赋0
bval(mm)=1-bval(mm);
end
%输出
plot(Bfit1);
xlabel('迭代次数');
ylabel('寻找的最大值结果');
title('适应度进化曲线');
bestv %输出最优适应度值
optxx %输出最优参数
bestv =
8
optxx =
2 -1
求最小值时将
[fmax,indmax]=max(func); %求当代最佳个体改成[fmax,indmax]=min(func); %求当代最佳个体即可。
python代码
参考文章:遗传算法详解 附python代码实现
初始化群体
# 初始化群体
DNA_SIZE = 5 # DNA长度,x1,x2各5个,长度越长精度越高
POP_SIZE = 50 # 初始种群数
CROSSOVER_RATE = 0.95 # 交叉概率
MUTATION_RATE = 0.001 # 变异概率
N_GENERATIONS = 30 # 迭代次数
X1_BOUND = [-1, 2] # x1自变量范围
X2_BOUND = [-1, 2] # x2自变量范围
适应度函数
def F(x1, x2):
return 3 * x1 - 2 * x2
3D图显示
def plot_3d(ax):
X = np.linspace(*X1_BOUND, 100)
Y = np.linspace(*X2_BOUND, 100)
X, Y = np.meshgrid(X, Y)
Z = F(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
ax.set_zlim(-10, 10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(3)
plt.show()
计算适应值
def get_fitness(pop):
x1, x2 = translateDNA(pop)
pred = F(x1, x2)
return (pred - np.min(pred)) + 1e-3
'''
减去最小的适应度是为了防止适应度出现负数,
通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],
最后在加上一个很小的数防止出现为0的适应度
'''
解码过程
# 解码过程
# pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
def translateDNA(pop):
x1_pop = pop[:, 1::2] # 前DNA_SIZE位表示x1
x2_pop = pop[:, ::2] # 后DNA_SIZE位表示x2
# pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
x1 = x1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X1_BOUND[1] - X1_BOUND[0]) + X1_BOUND[0]
x2 = x2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X2_BOUND[1] - X2_BOUND[0]) + X2_BOUND[0]
return x1, x2
交叉过程
# 交叉过程
def crossover_and_mutation(pop, CROSSOVER_RATE=CROSSOVER_RATE):
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father # 孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
变异过程
# 变异过程
def mutation(child, MUTATION_RATE=MUTATION_RATE):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE * 2) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1 # 将变异点的二进制为反转
选择适应值大的个体
# 选择适应值高的个体
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,p=(fitness) / (fitness.sum()))
return pop[idx]
计算结果
def print_info(pop):
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
x1, x2 = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("最优变量为:(x1, x2) = ", (x1[max_fitness_index], x2[max_fitness_index]))
print("最优解为:F(x1, x2) = {:.3f}".format(F(x1[max_fitness_index], x2[max_fitness_index])))
完整代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pylab # 显示3d动态显示
# %matplotlib auto
# %matplotlib notebook
# 初始化群体
DNA_SIZE = 5 # DNA长度,x1,x2各5个,长度越长精度越高
POP_SIZE = 50 # 初始种群数
CROSSOVER_RATE = 0.95 # 交叉概率
MUTATION_RATE = 0.01 # 变异概率
N_GENERATIONS = 30 # 迭代次数
X1_BOUND = [-1, 2] # x1自变量范围
X2_BOUND = [-1, 2] # x2自变量范围
# 适应度函数
def F(x1, x2):
return 3 * x1 - 2 * x2
# 画3D图
def plot_3d(ax):
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X = np.linspace(*X1_BOUND, 100) # 将自变量X1_BOUND均等分100个点
Y = np.linspace(*X2_BOUND, 100) # 将自变量X2_BOUND均等分100个点
X, Y = np.meshgrid(X, Y) # 将两个一维数组变成二维数组
Z = F(X, Y) # 调用适应度函数
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
ax.set_zlim(-10, 10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(2)
plt.show()
# 计算适应值
def get_fitness(pop):
x1, x2 = translateDNA(pop)
pred = F(x1, x2)
return (pred - np.min(pred)) + 1e-3
'''
减去最小的适应度是为了防止适应度出现负数,
通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],
最后在加上一个很小的数防止出现为0的适应度
'''
# 解码过程
# pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
def translateDNA(pop):
x1_pop = pop[:, 1::2] # 前DNA_SIZE位表示x1
x2_pop = pop[:, ::2] # 后DNA_SIZE位表示x2
# pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
x1 = x1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X1_BOUND[1] - X1_BOUND[0]) + X1_BOUND[0]
x2 = x2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X2_BOUND[1] - X2_BOUND[0]) + X2_BOUND[0]
return x1, x2
# 交叉过程
def crossover_and_mutation(pop, CROSSOVER_RATE=CROSSOVER_RATE):
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father # 孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
# 变异过程
def mutation(child, MUTATION_RATE=MUTATION_RATE):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE * 2) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1 # 将变异点的二进制为反转
# 选择适应值高的个体
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,p=(fitness) / (fitness.sum()))
return pop[idx]
# 计算结果
def print_info(pop):
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
x1, x2 = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("最优变量为:(x1, x2) = ", (x1[max_fitness_index], x2[max_fitness_index]))
print("最优解为:F(x1, x2) = {:.3f}".format(F(x1[max_fitness_index], x2[max_fitness_index])))
# 主函数
if __name__ == "__main__":
fig= plt.figure()
ax=fig.add_subplot(111,projection='3d')
plt.ion() # 将画图模式改为交互模式,程序遇到plt.show不会暂停,而是继续执行
plot_3d(ax)
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2)) # matrix (POP_SIZE, DNA_SIZE)
for i in range(N_GENERATIONS): # 迭代N代
x1, x2 = translateDNA(pop)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x1, x2, F(x1, x2), c='black', marker='o')
ax.set_title(f'迭代第{i + 1}次,一共要迭代{N_GENERATIONS}次')
plt.show()
plt.pause(0.1)
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
# F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
fitness = get_fitness(pop)
pop = select(pop, fitness) # 选择生成新的种群
print_info(pop)
# 显示前关掉交互模式
# 在plt.show()之前一定不要忘了加plt.ioff(),如果不加,界面会一闪而过,并不会停留。
plt.ioff()
plot_3d(ax)
最优的基因型: [0 1 0 1 0 1 0 1 0 1]
最优变量为:(x1, x2) = (2.0, -1.0)
最优解为:F(x1, x2) = 8.000
当求解最小值的问题时,把计算适应值函数改成如下结果即可:
def get_fitness(pop):
x,y = translateDNA(pop)
pred = F(x, y)
return np.max(pred) - pred + 1e-3