【论文】解读Deep Neural Networks for Learning Graph Representations
Deep Neural Networks for Learning Graph Representations
摘要
本文提出了一个新颖的学习图表示的模型,它可以对每个节点通过抓取图结构信息得到一个低维的向量表示。不同于前任的研究,我们采用一个‘随机冲浪模型’(random surfing model)去直接抓取结构信息,而不是使用Perozzi等人提出的基于采样方法的生成的线性序列。我们方法的优势将从理论和经验的角度来说明。
我们还为Levy和Goldberg (2014)提出的矩阵分解方法提供了一个新的视角,其中点互信息(PMI)矩阵(pointwise mutual information matrix)被认为是Mikolov等人(2013)提出的负采样’skip-gram model’的目标函数的解析解.与他们使用SVD从PMI矩阵中找到低维投影的方法不同,我们的模型中引入了堆叠的去噪自动编码器(the stacked denoising autoencoder)来提取复杂特征和模型非线性性。
为了证明我们的模型的有效性,我们在聚类和可视化任务上进行实验,使用所学的顶点表示作为特征。在不同规模数据集上的实验结果表明,我们的模型在此类任务中优于其他最新模型。
1 Introduction
图形是许多现实问题中用于信息管理的常见表示。例如,在蛋白质网络研究中,从蛋白质-蛋白质相互作用网络中挖掘蛋白质复合物在描述同源蛋白质的功能多样性方面起着重要作用,并提供有价值的进化见解,这本质上是一个聚类问题。因此,开发自动算法从图形中提取有用的深层信息至关重要。组织与潜在的大而复杂的图相关联的这种信息的有效手段之一是学习图表示,其将低维密集向量表示分配给图的每个顶点,编码由图传达的有意义的信息
(前略)虽然已经确定了学习线性结构的良好表示的高效且有效的方法,处理具有丰富拓扑结构的图结构更加复杂。为此,一种自然的方法是确定有效的方法,将学习图结构的顶点表示的任务转化为从线性结构学习表示的任务。Perozzi等人(2014)提出的DeepWalk提出了一种通过截断随机游走(truncated random walk)的均匀采样的方法将未加权图转换成线性序列集合的思想。在他们的方法中,采样顶点序列(sampled vertex sequences)描绘了图中顶点之间的连接的特征。这一步可以理解为将一般的图形结构转换成大量线性结构集合的过程。接下来,他们利用Mikolov等人(2013)提出的skip-gram model从这种线性结构中学习顶点的低维表示。学习的顶点表示在一些任务中是有效的,优于以前的一些方法,如谱聚类和模块化方法。
思考:虽然这种学习未加权图的顶点表示的方法是有效的,但仍有两个重要问题有待解决。第一,对于加权图,如何更准确、更直接地捕捉图的结构信息?第二,有没有更好的表示线性结构顶点的方法?
为了回答第一个问题,我们设计了一个适用于加权图的随机冲浪模型,它可以直接产生一个概率共现矩阵(probailistic co-occurrence matrix)。这种矩阵类似于通过从图中采样线性序列获得的共生矩阵(co-occurrence matrix),但是在我们的方法中不需要采样过程。
为了回答第二个问题,我们首先重温一种用于学习线性结构的顶点表示的流行的现有方法。Levy and Goldberg(2014)最近的一项研究表明,使用负采样方法优化与skip-gram相关的目标函数与分解单词及其上下文的正点互信息(positive pointwise mutual information)(PPMI)矩阵有内在联系。具体来说,他们表明可以使用标准奇异值分解(SVD)方法来分解PPMI矩阵,以从分解的矩阵中归纳出顶点(单词)表示。我们最近的方法被称为GraRep已被证明在学习图形表示的任务上取得了良好的实证结果。然而,该方法采用奇异值分解进行线性降维,而没有探索更好的非线性降维技术。
本文对Levy and Goldberg(2014)的工作给予了新的视角。我们认为,原始PPMI矩阵本身是图的显式表示矩阵,奇异值分解步骤本质上起到了降维工具箱的作用。虽然诱导最终单词表示的奇异值分解步骤被证明是有效的,但Levy等人(2015)也证明了使用PPMI矩阵自身作为单词表示的有效性。有趣的是,如作者所示,从奇异值分解方法中获得的表示不能完全优于PPMI矩阵本身的表示(Levy,Goldberg和Dagan2015)。由于我们的最终目标是有效捕捉图形信息的顶点表示,因此有必要研究从PPMI矩阵中恢复顶点表示的更好方法,其中可以捕捉不同顶点之间潜在的复杂非线性关系。
深度学习揭示了非线性复杂现象建模的途径,在不同领域有许多成功的应用,如语音识别(Dahl等人,2012年)和计算机视觉(Krizhevsky,Sutskever,和Hinton,2012年)。深度神经网络(DNN),例如堆叠式自动编码器,可被视为从低级特征学习高级抽象的有效方法。这个过程本质上执行降维,将数据从高维空间映射到低维空间。与(截断的)基于奇异值分解的降维方法不同,基于奇异值分解的降维方法通过线性投影从原始表示空间映射到具有较低秩的新空间,深度神经网络(如堆叠自动编码器)可以学习高度非线性的投影。事实上,Tian等人(2014)最近的工作在聚类任务中使用稀疏自动编码器来代替谱聚类的特征值分解步骤,并且他们实现了显著的改进。受他们工作的启发,我们还研究了使用基于深度学习的替代方法从原始数据表示中学习低维表示的有效性。与他们的工作不同,我们的目标是学习一般图的顶点表示,而不是专门关注聚类任务。我们将深度学习方法应用于PPMI矩阵,而不是他们模型中使用的拉普拉斯矩阵。前者已被证明有潜力产生比后者更好的代表性(佩罗齐,阿尔福和斯基纳,2014年)。为了增强我们的模型的鲁棒性,我们还使用堆叠去噪自动编码器来学习多层表示。
称我们提出的模型为DNGR(deep neural networks for graph representations)。学习的表示可以被视为输入特征,其可以被馈送到其他任务,例如无监督聚类和有监督分类任务。为了验证我们模型的有效性,我们进行了实验,将学习到的表示用于一系列不同的任务,其中考虑了不同风格和拓扑的真实世界网络。为了进一步证明我们的模型在考虑更简单、更大规模的实际图形结构时的有效性,我们在一个非常大的语言数据集上应用了我们的算法,并在单词相似性任务上进行了实验。在所有这些任务中,我们的模型优于其他学习图形表示的方法,并且我们的模型也是可并行的。我们的主要贡献有两个方面:
- 理论上,我们认为深度神经网络提供了能够捕获由图形传达的非线性信息的优势,而这种信息不容易被许多广泛使用的传统线性降维方法捕获。此外,我们认为我们的随机冲浪模型可以用来取代广泛使用的传统的基于抽样的方法来收集图形信息。
- 根据经验,我们证明了我们的新模型能够更好地学习加权图的低维顶点表示,其中可以捕获图的有意义的语义、关系和结构信息。我们表明,所得到的表示可以有效地用作不同下游任务的特征。
2 Background and Related Work
在这一节中,我们首先介绍了DeepWalk中提出的未加权图的随机采样,以说明将顶点表示转换为线性表示的可行性。接下来,我们考虑两种单词表示方法:负采样skip-gram和基于PPMI矩阵的矩阵分解。这些方法可以被视为从线性结构数据中学习单词表示的线性方法。
Notation给定一个加权图 G = < V , E > G=
2.1 Random Walk in DeepWalk
DeepWalk提供了一种有效的方法,称为截断随机行走(truncated tandom walk),将未加权的图结构信息转换成线性序列,表示图的顶点之间的关系。所提出的随机游走是一种适用于未加权图的均匀抽样方法。他们首先从图中随机选择一个顶点 v 1 v_1 v1,并将其标记为当前顶点,然后从当前顶点 v 1 v_1 v1的所有邻居中随机选择下一个顶点 v 2 v_2 v2。现在,他们将这个新选择的顶点 v 2 v_2 v2标记为当前顶点,并重复这样的顶点采样过程。当一个序列中的顶点数达到一个称为行走长度 η \eta η的预设数时,算法终止。在重复上述过程 γ \gamma γ次(称为完全行走)后,收集线性序列的组块。
虽然截断随机游走是用线性序列表示未加权图结构信息的一种有效方法,但这一过程涉及缓慢的采样过程,超参数 η \eta η和 γ \gamma γ不易确定。我们注意到深度行走产生了一个基于采样线性序列的共生矩阵(co-occurrence matrix)。在第三节中,我们描述了我们的随机冲浪模型(random surfing model),它直接从一个加权图中构造一个概率共现矩阵(probabilistic co-occurrence matrix),避免了昂贵的采样过程。
2.2 Skip-gram with Negative Sampling
自然语言语料库由线性序列的词流组成。最近,神经嵌入方法和基于矩阵分解的方法已被广泛用于学习单词表示。在(Mikolov等人,2013)中提出的skip-gram model已被证明是一种有效和高效的学习单词表示的方法。两个值得注意的方法来改进skip-gram model是负采样**(SGNS)**(skip-gram with negative sampling)和分层softmax。在本文中,我们选择使用前一种方法。
在SGNS中,噪声对比估计(NCE)(noise contrastive estimation)方法的简化变体被用来增强skip-gram model的鲁棒性。SGNS根据先验的单词分布随机创建负对 ( w , c N ) (w,c_N) (w,cN)),并尝试使用低维向量来表示每个单词 w ∈ V w\in V w∈V 和上下文单词 c ∈ V c\in V c∈V对。SGNS的目标函数旨在最大化正对 ( w , c ) (w,c) (w,c),最小化负对(w,cN)。
arg max w ⃗ , c ⃗ log σ ( w ⃗ ⋅ c ⃗ ) + λ ⋅ E c N ∼ P D [ log σ ( − w ⃗ ⋅ c N ⃗ ] \argmax_{\vec{w},\vec{c}}\log\sigma (\vec{w}\cdot \vec{c})+\lambda \cdot \mathbb{E}_{c_N\sim P_D}[\log \sigma (-\vec{w}\cdot \vec{c_N}] w,cargmaxlogσ(w⋅c)+λ⋅EcN∼PD[logσ(−w⋅cN]
where σ ( ⋅ ) \sigma(\cdot) σ(⋅)是sigmoid函数,定义为 σ ( x ) = ( 1 + e − x ) − 1 \sigma(x)=(1+e^{-x})^{-1} σ(x)=(1+e−x)−1,且 λ \lambda λ是负样本的个数。 E c N ∼ P D [ ⋅ ] \mathbb{E}_{c_N\sim P_D}[\cdot] EcN∼PD[⋅]是从负抽样 c N c_N cN中获得的实例符合分布 p D = # ( c ) ∣ D ∣ p_D=\frac{\#(c)}{|D|} pD=∣D∣#(c)的分布时的期望。(unigram c在数据集D中的分布)
2.3 PMI matrix and SVD
学习图形表示(尤其是单词表示)的另一种方法是基于矩阵分解技术。这种方法基于全局共现计数(global co-occurrence counts)的统计来学习表示,并且在某些预测任务中可以优于基于单独的局部上下文窗口的神经网络方法。
矩阵分解方法的一个例子是超空间模拟分析(hyperspace analogue ananlysis)(Lund和Burgess 1996),它分解单词-单词共现矩阵以产生单词表示。这种方法和相关方法的一个主要缺点是,诸如停止词(stop words)之类的具有相对较小语义值的频繁词对所生成的词表示具有不成比例的影响。Church and Hanks’ 的逐点互信息矩阵被提出来解决这个问题,并已被证明提供了更好的单词表示:
P M I w , c = log ( # ( w , c ) ⋅ ∣ D ∣ # ( w ) ⋅ ( c ) ) PMI_{w,c}=\log(\frac{\# (w,c)\cdot |D|} {\#(w) \cdot (c)}) PMIw,c=log(#(w)⋅(c)#(w,c)⋅∣D∣)
wher, ∣ D ∣ = ∑ w ∑ c # ( w , c ) |D|=\sum_w\sum_c\#(w,c) ∣D∣=∑w∑c#(w,c)
提高表现的一种常见方法是将每个负值指定为0,详见(Levy and Goldberg 2014),以形成PPMI矩阵
X w , c = max ( P M I w , c , 0 ) X_{w,c}=\max(PMI_{w,c},0) Xw,c=max(PMIw,c,0)
where , X X X是PPMI矩阵。
虽然PPMI矩阵是一个高维矩阵,但使用截断奇异值分解方法进行降维(Eckart和Y oung 1936)产生了关于L2损失的最优秩因子分解(Levy和Goldberg 2014)。我们假设矩阵 X X X可以分解为三个矩阵 U Σ V T U\Sigma V^T UΣVT,其中 U U U和 V V V是正交矩阵, Σ \Sigma Σ是对角矩阵。换句话说
X ≈ X d = U d Σ d V d T X\approx X_d=U_d\Sigma_d V_d^T X≈Xd=UdΣdVdT
herer, U d U_d Ud和 V d V_d Vd是 U U U和 V V V的左侧 d d d列对应于(in Σ d \Sigma_d Σd)前-d个奇异值。根据Levy等人(2015)的观点,单词表示矩阵 R R R可以是
R = U d ( Σ d ) 1 / 2 o r R = U d R=U_d(\Sigma_d)^{1/2} \ or \ R=U_d R=Ud(Σd)1/2 or R=Ud
PPMI矩阵 X X X是单词表示矩阵和上下文矩阵的乘积。奇异值分解过程为我们提供了一种从矩阵 X X X中找到矩阵 R R R的方法,其中 R R R的行向量,即单词/顶点的低维表示,可以通过从给出的它们的高维表示(即给定的 X X X)进行线性投影来获得,。我们认为这种投影不一定是线性投影。在这项工作中,我们研究了使用非线性投影方法来取代线性奇异值分解方法,通过使用深度神经网络。
2.4 Deep Neural Networks
深度神经网络可以用于学习多层次的特征表示,在不同领域取得了成功的结果。训练这样的网络被证明是困难的。一个有效的解决方案,,是使用贪婪分层无监督预训练(greedy layer-wise unsupervised pre-trainning)。该策略旨在一次学习每一层的有用表示。然后,学习的低级表示被馈送作为后续表示学习的下一层的输入。神经网络通常采用非线性激活函数(如sigmoid或tanh)来捕捉从输入到输出的复杂非线性投影。
为了训练一个包含多层特征表示的深层体系结构,自动编码器已经成为常用的构件之一。自动编码器执行两个动作——编码步骤(encoding),然后是解码步骤(decoding)。在编码步骤中,将函数 f θ 1 ( ⋅ ) f_{\theta_1}(\cdot) fθ1(⋅)应用于输入空间中的向量,并将其发送到新的特征空间。在这个过程中,通常会涉及一个激活函数来模拟两个向量空间(输入向量空间和潜在向量表示空间)之间的非线性。在解码步骤,重建函数 g θ 2 ( ⋅ ) g_{\theta_2}(\cdot) gθ2(⋅)用于从潜在表示空间重建原始输入向量。
我们假设 f θ 1 ( x ) = σ ( W 1 x + b 1 ) f_{\theta_1}(x)=\sigma (W_1x+b_1) fθ1(x)=σ(W1x+b1)和 g θ 2 ( y ) = σ ( W 2 y + b 2 ) g_{\theta_2}(y)=\sigma(W_2y+b2) gθ2(y)=σ(W2y+b2),其中 σ ( ) \sigma() σ()是激活函数, θ 1 = { W 1 , b 1 } \theta_1= \{W_1,b_1\} θ1={W1,b1}是编码器涉及的权重(参数), θ 2 = { W 2 , b 2 } \theta_2= \{W_2,b_2\} θ2={W2,b2}是解码器涉及的权重(参数)。这里, W 1 W_1 W1和 W 2 W_2 W2是将输入空间变换向量的线性映射(矩阵), b 1 b_1 b1和 b 2 b_2 b2是偏置向量。我们的目标是通过求 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2来最小化以下重建损失函数:
∑ i L ( x ( i ) , g θ 2 ( f θ 1 ( x ( i ) ) ) ) \sum_i L(x^{(i)},g_{\theta_2}(f_{\theta_1}(x^{(i)}))) i∑L(x(i),gθ2(fθ1(x(i))))
where, L L L是 样本对(sample-wise)损失,且 x ( i ) x^{(i)} x(i)是第 i i i个实例。
堆叠式自动编码器是由多层这种自动编码器组成的多层深层神经网络。堆叠式自动编码器使用逐层训练方法来提取基本规则,逐层从数据中捕获不同级别的抽象,更高层从数据中传达更高级别的抽象。
3 DNGR Model
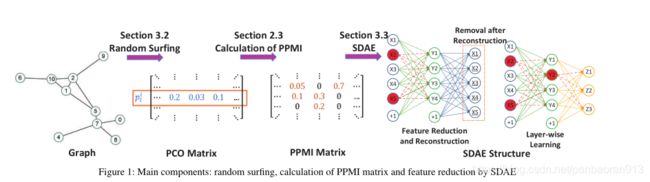
我们现在详细介绍我们的DNGR模型。如图1所示,该模型由三个主要步骤组成。首先,我们引入随机冲浪模型(第3.1节)来捕获图形结构信息并生成概率共现矩阵。接下来,我们根据我们的概率共现矩阵计算PPMI矩阵,如下所示(Bullinaria和Levy 2007)(见第2.3节)。之后,使用堆叠去噪自动编码器(第3.2节)来学习低维顶点表示.
3.1 Random Surfing and Context Weighting
虽然有效,但是用于将图结构转换成线性序列的采样方法有一些弱点。首先,采样序列的长度是有限的。这使得很难捕捉出现在采样序列边界的顶点的正确上下文信息。其次,确定某些超参数(如行走长度(walk length) η \eta η和总行走(total walks) γ \gamma γ)并不简单,尤其是对于大型图。
为了解决这些问题,我们考虑使用一个随机冲浪模型,该模型由用于任务排序的PageRank模型驱动。我们首先随机排列图中的顶点。我们假设我们当前的顶点是第 i i i个顶点,并且有一个转移矩阵 A A A捕获不同顶点之间的转移概率。
我们引入一个行向量(row vector) p k p_k pk,它的第 j j j个条目表示经过 k k k步转换后到达第 j j j个顶点的概率, p 0 p_0 p0是初始化的 1-hot vector,第 i i i个条目的值为1,其他值为0. 我们重新考虑一个随机冲浪模型:再每个时间,有一个概率 α \alpha α随机冲浪的过程将继续,和一个 1 − α 1-\alpha 1−α将返回到原始顶点并重新开始该过程。这导致以下循环:
p k = α ⋅ p k − 1 A + ( 1 − α ) p 0 p_k=\alpha\cdot p_{k-1}A+{(1-\alpha)}p_0 pk=α⋅pk−1A+(1−α)p0
如果假设我们在过程中没有随机重启,那么在正好 k k k步转换之后到达不同顶点的概率由下式指定:
p k ∗ = p k − 1 ∗ A = p o A k p_k^*=p_{k-1}^*A=p_oA^k pk∗=pk−1∗A=poAk
直觉上,两个顶点之间的距离越近,他们之间应该有越亲密的关系。因此,基于上下文节点到当前节点的相对距离来权衡上下文节点的重要性是合理的。这种加权策略在word2vec 和Glo Ve 中都有实施,并被发现对获得良好的实证结果很重要。基于这一事实,我们可以看到,理想情况下,第 i i i个顶点的表示应该以下列方式构造:
r = ∑ k = 1 K w ( k ) ⋅ p k ∗ r=\sum^K_{k=1}w(k)\cdot p_k^* r=k=1∑Kw(k)⋅pk∗
where w ( ⋅ ) w(\cdot) w(⋅)是一个下降函数(decreasing function),即 w ( t + 1 ) < w ( t ) w(t+1)
我们认为以下基于上述随机冲浪过程构造顶点表示的方式实际上满足上述条件:
r = ∑ k = 1 K p k r=\sum^K_{k=1}p_k r=k=1∑Kpk
事实上,可以证明我们有以下几点:
p k = α k p k ∗ + ∑ t = 1 k α k − 1 ( 1 − α ) p k − t ∗ p_k=\alpha^kp_k^*+\sum^k_{t=1}\alpha^{k-1}(1-\alpha)p_{k-t}^* pk=αkpk∗+t=1∑kαk−1(1−α)pk−t∗
where p 0 ∗ = p 0 p_0^*=p_0 p0∗=p0. r 中 的 p t ∗ r中的p_t^* r中的pt∗的系数为:
w ( t ) = α y + α t ( 1 − α ) ( K − t ) w(t)=\alpha^y+\alpha^t(1-\alpha)(K-t) w(t)=αy+αt(1−α)(K−t)
where w ( t ) 是 一 个 下 降 函 数 , 因 为 w(t)是一个下降函数,因为 w(t)是一个下降函数,因为\alpha<1$.虽然skip-gram中的加权函数可以描述为
w ′ ( t ) = − t K + ( 1 + 1 K ) w'(t)=-\frac{t}{K}+(1+\frac{1}{K}) w′(t)=−Kt+(1+K1)
且 Glo Ve的权重函数为:
w ′ ′ ( t ) = 1 t w''(t)=\frac{1}{t} w′′(t)=t1
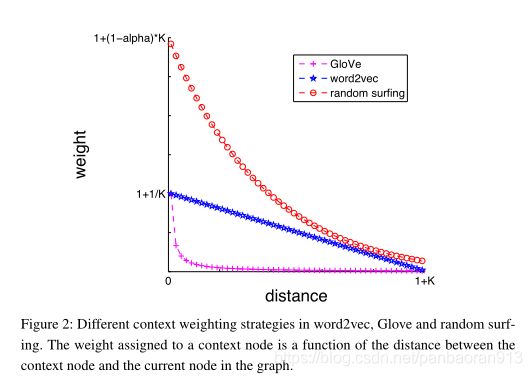
从图2中我们可以看到,所有的加权函数都是单调递减的函数。类似于word2vec和GloV e,我们的模型还允许根据上下文信息到目标的距离对其进行不同的加权,这在以前被证明对于构建良好的单词表示很重要。我们将通过实验来评估这方面的重要性。
3.2 Stacked Denoising Autoencoder
我们的研究旨在研究从传达图形基本结构信息的PPMI矩阵为顶点构造高质量的低维向量表示。奇异值分解过程虽然有效,但本质上只能产生从PPMI矩阵包含的矢量表示映射到最终低维顶点矢量表示的线性变换。我们相信在两个向量空间之间可能建立非线性映射。因此,我们使用堆叠去噪自动编码器,一种在深度学习中使用的流行模型,从原始的高维顶点向量生成压缩的低维向量。
如表1所述,我们首先初始化神经网络的参数,然后使用贪婪的分层训练策略来学习每一层的高级抽象(high-level abstractions)。为了增强DNN的鲁棒性,我们使用堆叠去噪自动编码器(SDAE)。与传统的自动编码器不同,去噪自动编码器在进行训练步骤之前会部分破坏输入数据。具体来说,我们通过以一定的概率将向量中的一些条目指定为0来随机破坏每个输入样本x(向量)。这个想法类似于对矩阵完成任务中缺失条目的建模,其目标是利用数据矩阵中的规律性,在某些假设下有效地恢复完整的矩阵.SDAE结构在fig1显示。 X i ′ X_i' Xi′对应于输入数据, Y i ′ Y_i' Yi′对应于第一层的学习表示,且 Z i ′ Z_i' Zi′是对应第二层的学习 表示。暂时损坏的节点(如: X 2 , X 5 , 和 Y 2 X_2,X_5,和Y_2 X2,X5,和Y2)用红色突出显示。
类似于标准的自动编码器,我们再次从潜在的表示中重构数据。换句话说,我们感兴趣的是:
min θ 1 , θ 2 ∑ i = 1 n L ( x ( i ) , g θ 2 ( f θ 1 ( x ~ ( i ) ) ) ) \min_{\theta_1,\theta_2}\sum_{i=1}^nL(x^{(i)},g_{\theta_2}(f_{\theta_1}(\tilde{x}^{(i)}))) θ1,θ2mini=1∑nL(x(i),gθ2(fθ1(x~(i))))
where, x ~ ( i ) \tilde{x}^{(i)} x~(i)是输入数据 x ( i ) x^{(i)} x(i)的损坏, L L L是标准平方损失。
3.3 Discussion of the DNGR Model
这里我们分析一下DNGR的优势。其经验有效性将在第4节中介绍.
- Random Surfing Strategy: 正如我们在第3.1节中分析的那样,随机冲浪过程克服了与以前工作中使用的采样过程相关的限制,并且它为我们提供了某些期望的属性,这些属性是以前嵌入模型的实现所共有的,例如word2vec和Glo Ve.
- Denoising Strategy:高维输入数据往往包含冗余信息和噪声。据信,去噪策略可以有效地降低噪声并增强鲁棒性。
- Efficiency:根据之前的分析,就图中的顶点数量而言,使用DNGR中使用的自动编码器进行推理的时间复杂度低于基于SVD的矩阵分解方法。奇异值分解的时间复杂度至少是顶点数的二次函数。然而,DNGR的推理时间复杂度与图中的顶点数成线性关系。
4. Datasets,Baselines
为了评估DNGR模型的性能,我们在真实数据集上进行了实验。除了显示图形表示的结果,我们还评估了从由线性序列组成的自然语言语料库中学习的单词嵌入的有效性。
4.1 Datasets
- 20-NewsGroup:包含大约20,000个新闻组文档,并根据类别分为20个不同的组。在我们的实验中,每个文档都是一个顶点,由一个通过TFIDF生成的词向量表示,两个文档之间的边的权重是两个文档的余弦相似度。为了证明我们的模型的稳健性,如(Tian等,2014)中所示,我们分别从3个、6个和9个不同的类别中构建了3个组,并从每个类别中随机选择了200个文档。在我们的实验中,我们选择了与(田等人,2014)中使用的相同的类别。这三个网络分别由包含200、400和600个文档的全连通加权图表示。
- Wine:来自UCI机器学习知识库(李奇曼,2013)的数据集是对生长在意大利同一地区但来自三个不同品种的葡萄酒进行化学分析的结果。该分析确定了3种葡萄酒中每一种的13种成分的数量,包括178个实例。接下来(田等人,2014),我们使用两个不同实例的余弦相似性作为边权重,标签作为基础事实来构建图。
- Wikipedia Corpus:是一个免费开放的在线百科全书。我们选取了黄等(2012)中使用的2010年4月的快照作为学习单词表征的训练语料。数据集有200万篇文章和9.9亿个令牌。为了证明深度学习相对于奇异值分解的有效性,我们选择了一个包含10,000个最频繁单词的字典(由于奇异值分解算法的时间复杂性,选择了10,000个单词)。
为了评估由每种算法生成的单词表示的性能,我们在4个数据集上进行了单词相似性实验(Mikolov等人,2013),包括流行的单词353 (Finkelstein等人,2001)、单词相似性(Zesch,Müller和Gurevych,2008)和单词相关度(Agirre等人,2009)和MC (Miller和Charles,1991),如在(Pennington,Socher和Manning,2014)中使用的那样;Levy,Goldberg,和Dagan 2015)。所有数据集都有词对和人为指定的相似性。
4.2 Baseline Algorithms
我们考虑以下四种基线算法.
- DeepWalk:是最近提出的学习网络表示的方法。它通过截尾随机游动将图结构转换成线性序列,并使用具有分层softmax的skip-gram对序列进行处理。
- SGNS:是在word2vec中提出的。它适用于捕捉线性结构。SGNS已被证明是一种从理论和实验上学习词汇表征的有效模式。
- PPMI:是信息论中常用的一种度量。PPMI在(Levy,Goldberg和Dagan 2015)中用于单词表示,是一种稀疏的高维表示。
- SVD:是一种常用的矩阵分解方法,用于降维或提取特征。接下来(Levy和Goldberg 2014),我们使用奇异值分解来压缩PPMI矩阵以获得低维表示。
5.Experiments
5.1 Parameters
在基线系统中,我们设置行走长度 η = 40 \eta=40 η=40,总行走 γ = 80 ∗ ∣ V ∣ \gamma=80* |V| γ=80∗∣V∣,其中 ∣ V ∣ | V | ∣V∣是图顶点的数量,如(Perozzi,Al-Rfou和Skiena 2014)中所建议的。为了达到每个基线算法的最佳性能,我们为DeepWalk和SGNS设置了负样本 λ = 5 \lambda=5 λ=5,上下文窗口大小 K = 10 K = 10 K=10,如(Levy,Goldberg和Dagan,2015)中所述。对于我们的模型,我们调整了dropout ratio,这减少了优化过程中的误差。如表2所列,3NG和6NG的神经网络有3层,9NG和Blogcatalog有4层。所有神经元均由sigmoid激活。
5.2 Experiments
针对每种基线算法,我们给出了我们提出的方法的经验结果。结果证明了通过我们的随机冲浪过程使用加权策略的优势和深度架构的有效性。我们的源代码将在http://shelson.top发布
5.2.1 Clustering Task on the 20-NewsGroup Network
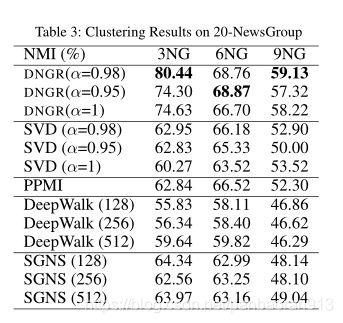
在这个实验中,我们运行每个基线算法来为每个顶点生成一个表示向量,该向量用作聚类的特征表示。我们使用了K-means算法(Arthur和V assilvitskii,2007)和归一化互信息(NMI)(斯特雷尔,戈什和穆尼,2000)作为衡量性能的指标。我们用不同的初始化运行每个算法10次,并在表3中报告了平均分数。为了说明不同维度的影响,我们还列出了DeepWalk和SGNS的128和512个维度的结果。
从结果可以看出,我们的DNGR模型明显优于其他基线算法,尤其是当 α = 0.98 \alpha=0.98 α=0.98时。当 α = 1 \alpha=1 α=1时,上下文信息不会根据它们的距离进行加权,我们获得了较低的结果,这证实了第3.1节中讨论的加权策略的重要性。增加DeepWalk和SGNS中使用的维度并没有导致分数的一致提高。比较DNGR和PPMI,分数的提高证明了提取有意义信息和降低稀疏高维矩阵维数的好处。在相同的 α \alpha α设置下,DNGR始终比SVD给出更好的结果。这为我们之前的讨论提供了经验证据——奇异值分解并不总是优于PPMI的事实表明,可能需要一种更好的降维方法。
5.2.2 Visualization of Wine
评估顶点表示质量的另一种方法是通过可视化。通过后续的可视化实验(唐等,2015)比较了DNGR与SVD、deepwalk和SGNS在Wine上的性能。顶点表示矩阵作为特征被输入到t-SNE(V . an der Maaten and Hinton 2008),它将所有的点映射到一个2D空间,在该空间中,相同类型的葡萄酒用相同的颜色突出显示。在相同的设置下,不同颜色组之间边界更清晰的聚类表示更好的表示。

从图3中,我们可以看到DeepWalk和SGNS的输出可视化显示了不清晰的边界和扩散的集群。DNGR( α = 1 \alpha=1 α=1)好很多。虽然SVD优于DNGR( α = 1 \alpha=1 α=1),但在结果中我们可以看到绿点仍然与一些红点混合在一起。DNGR( α = 0.98 \alpha=0.98 α=0.98)是明显的赢家。我们可以看到,不同颜色的点出现在3个不同的极点,同一颜色的大多数点聚集在一起。
5.2.3 Word Similarity Task
为了进一步理解我们的DNGR模型的深度学习组件的有效性,我们在大规模语言语料库上进行了实验,在那里我们从大型线性结构化图形数据中学习单词表示。在这个实验中,由于数据由严格的线性序列组成,所以不需要随机冲浪过程。相反,我们可以直接从训练语料库中统计单词对。为了比较不同算法的性能,我们在标准数据集上对单词相似性任务进行了评估。斯皮尔曼的等级相关系数(Zar 1972)被用来评估算法产生的结果。根据(Levy,Goldberg和Dagan 2015)中报告的发现,为了获得最佳结果,我们将SGNS,DNGR和SVD的阴性样本数分别设置为5,1,1。
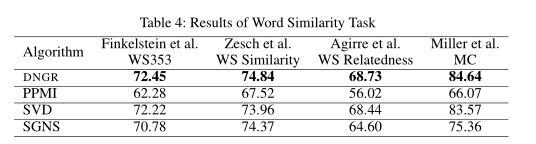
如表4所示,DNGR的性能超过了其他基线算法。SVD和DNGR产生的结果都比PPMI好得多,证明了降维在这项任务中的重要性。在所有数据集上,DNGR的性能都高于SVD和SGNS,这揭示了在学习表示时捕获复杂的非线性规律的重要性,并说明了使用我们的深度学习方法学习更好的抽象的能力。
5.2.4 Importance of Deep Structures
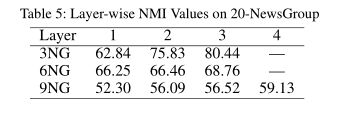
为了理解深层结构的必要性,我们进一步测量了20-新闻组的分层NMI值。对于3NG和6NG,我们使用3层神经网络来构建表示,对于9NG,我们使用4层,如表2所示。从表5中,我们可以看出,对于所有三个网络,性能总体上从浅层向深层增加,这表明了深层结构的重要性。
6. Conclusion
在本文中,我们提出了一个深度图表示模型,用于将每个顶点编码为低维向量表示。我们的模型展示了堆叠去噪自动编码器在提取有意义的信息和生成信息表示方面的能力。我们在不同任务的真实数据集上进行了实验,实验结果表明,该模型的性能优于几种先进的基线算法。虽然调整神经网络超参数的过程需要努力和专业知识,但我们得出结论,通过深度学习探索数据的底层结构可以改善图形的表示。