算法(一):算法复杂度之时间复杂度和空间复杂度
目录
概念
复杂度分析
时间复杂度分析
空间复杂度分析
总结
概念
算法复杂度:是指算法在编写成可执行程序后,运行时所需要的资源,包括时间资源(运行算法耗费的时间)和内存资源(程序运行占用的内存大小)。它是一个衡量算法优劣的重要指标,按照所需资源的又细分为时间复杂度和空间复杂度。
时间复杂度:运行算法所需的时间随着数据量变化关系,记做T(n),n为算法的规模。
空间复杂度:一个算法在运行过程中临时占用存储空间大小的量度,记做S(n),n为算法的规模。
大O表示法:表示算法时间和空间复杂度的符号,通常表示为记做S(n)=O(f(n)),T(n)= O(f(n)),n为数据的规模,f(n)通常是一个函数,比如f(n)=2n+1;f(n)=n^2;f(n)=logn等等。而T(n)一般也是一个函数以数学来说,算法运行时间和n的对应关系就是一个函数曲线,随着n逐渐增大到很大很大,除去影响该曲线主要走势的的一些因素,比如函数中的常量,系数,提取出核心因素次方,开方,对数,这个核心因素所表示的函数形式成为该算法的渐进时间空间复杂度或渐进时间复杂度,又简称时间复杂度和空间复杂度。
复杂度分析
数据结构和算法本身解决的是“快”和“省”的问题,即如何让代码运行得更快,更省存储空间。所以执行效率是算法一个非常重要的考量指标。那如何来衡量你编写的算法代码的执行效率呢?这里就需要进行复杂度分析。
事后统计法:一种在实际情况下不同环境运行测试代码,比较测试结果的方法。不过有一些局限性,一是测试结果依赖测试环境:硬件环境影响测试结果,比如Intel Core i9 处理器和 Intel Core i3 处理器差异,二是测试结果受数据规模影响:测试规模太小的可能无法真实反映算法的性能。
因此,就产生了一种不用具体的测试数据,可以只需要粗略的估算算法性能的方法,这就是我们今天要说的空间复杂度和时间复杂度,对应的分析方法又可以划分时间复杂度分析法,空间复杂度分析法。
时间复杂度分析
在前面我们说过,时间复杂度的大O表示法为T(n)= O(f(n)),那么问题来了,这个公式是怎么得出来的呢,下面就来分析下。
渐进时间复杂度官方定义:若存在函数 f(n),使得当n趋近于无穷大时,T(n)/ f(n)的极限值为不等于零的常数,则称 f(n)是T(n)的同数量级函数。记作 T(n)= O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。渐进时间复杂度用大写O来表示,所以也被称为大O表示法。
那么,问题来了,一般我们可以粗略计算出数据量n和计算所需时间T的函数关系式,如何根据已知的函数关系式推出时间复杂度呢,推理规则重点如下:
- 如果运行时间是常数量级,就用1表示时间复杂度;
- 只保留时间函数中的最高阶项;
- 如果最高阶项存在,则省去最高阶项前面的系数。
时间复杂度O(1):一个方法里有四条语句,假设执行每一条语句的时间都是t,则时间和数据n的关系 T=4t。也就是说无论n怎么增加,运算的时间都是4t。同样的一个方法中语句数量为k的方法,T=kt,kt的值必然是一个常数,和n没有关系,像这种被称为常量级,根据推导公式第一条,运算时间是常量,则该T=kt的同量级函数为f(n)=1,则时间复杂度T(n)=O(1);
public void eat(int n){
System.out.println("1111");
System.out.println("2222");
System.out.println("3333");
System.out.println("4444");
}以函数图展示则如下,Y轴是时间复杂度,X轴是数据n的变化
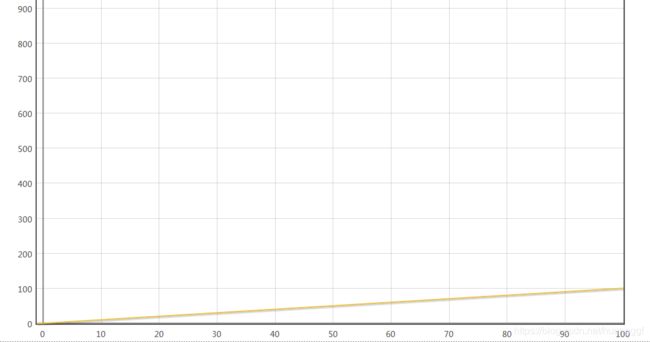
时间复杂度O(n):假设执行一条语句的时间为t,执行一次循环的时间为3t,执行n次循环的时间3tn,执行一次方法的时间为T=3tn+t,根据公式二,存在最高阶项n,所以只保留最高阶项,T=3tn;根据公式三,去除最高阶项的系数3t,则最终得到其同量级函数f(n)=n,时间复杂度公式为T(n)=O(n);
public void eat1(int n){
System.out.println("000");
for(int i=0; i以函数图展示则如下,Y轴是时间复杂度,X轴是数据n的变化,任数据变化,时间固定为常量
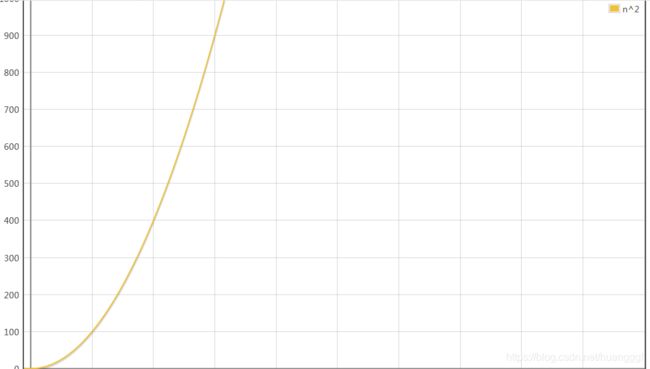
时间复杂度O(n²):假设执行一条语句的时间为t,则执行一次方法的时间T=t+n(3t+2tn),即T=t+3tn+2tn²,根据公式二出去t 3tn,根据公式三去除系数2t,最终得到同量级函数f(n)=n²;即时间复杂度T(n)=O(n²)
public void eat1(int n){
System.out.println("000");
for(int i=0; i对应的函数曲线如下:
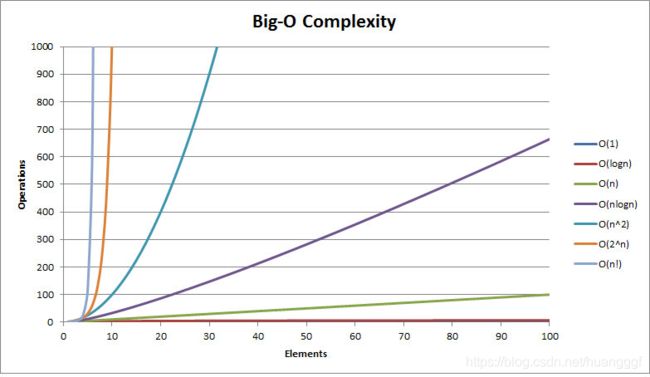
同理的,其他类型的时间复杂度函数如O(logn),O(2^n),O(n³)等就不再赘述了,直接上图:
空间复杂度分析
时间复杂度不是用来计算程序具体耗时的,空间复杂度也不是用来计算程序实际占用的空间的。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势。空间复杂度常用的有O(1)、O(n)、O(n²),相对时间复杂度,常用的种类比较少。大多数情况下,算法的时间运行效率才是最重要的。只要算法占用的存储空间不要达到计算机无法接受的程度即可。所以,常常通过牺牲空间复杂度来换取算法更加高效的运行时间效率。
算法在计算机存储器上占用的空间包括三个部分:
输入输出:算法的输入输出数据所占用的存储空间是通过参数表由调用函数传递而来的,它不会随算法的不同而改变。
算法本身:存储算法本身所占用的存储空间与算法的长短成正比,要压缩这部分存储空间,就必须编写出较短的算法。然而,算法想要实际应用需要根据需求采取不同的编程语言来实现,不同编程语言实现的代码长短差别很大,然而存储空间都在可接受范围之内。
临时内存:临时内存是运行算法时临时占用的内存空间,分为两类。一类是占用固定内存大小,不随着问题规模变化而变化,一种是随着问题规模变化而变化。
空间复杂度O(1):如下代码执行所需要的临时空间不随着变量n的大小而变化,即此空间复杂度为一个常量,代码中的 i、j、m 所分配的空间都不随着处理数据量变化,因此它的空间复杂度 S(n) = O(1);
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;空间复杂度O(n):这段代码中,第一行new了一个数组出来,这个数据占用的大小为n,这段代码的2-6行,虽然有循环,但没有再分配新的空间,因此,这段代码的空间复杂度主要看第一行即可,即 S(n) = O(n)
int[] aar = new int[n]
for(i=1; i<=n; ++i)
{
j = i;j++;
}总结
算法的复杂度分为时间复杂度和空间复杂度,大多数情况下,更加注重时间复杂度。
通常时间复杂度近似于算法运行时间时间曲线,在数据量或者说问题规模变得很大的时候,时间复杂度高的算法耗时就高,时间复杂度低的耗时就低,从最简答到最复杂依次为:O(1) 而复杂的程序代码,使用多层级的方式可以减少代码量,降低空间复杂度,层级少了较大可能需要多写代码,导致空间复杂度的提高,另外以我个人理解,对于空间的需求一般在算法初始化时就进行了预估和分配,在后续代码中虽然会产生少量临时变量,但是关键还是看初始化部分,这可能就是空间复杂度的分类比时间复杂度分类少得多。 辛辛苦苦敲了几天,拼拼凑凑加理解也算告一段落了,感谢读者的阅读,如有出入,请指正,谢谢!