Matlab 实现信号滤波

项目介绍

在此文章中，信号的导入、滤波以及时频转换将被介绍。

代码实现

1、导入信号

这里我们使用三种不同频率的信号的叠加信号。

clc
clear

fs = 1000;  % 重采样频率
T = 1/fs;  % 周期
n = 5;  % 1Hz频率被分成n段
N = fs*n;  % 因为1Hz频率被分成了n段，所以频谱的x轴数组有fs*n个数
f = (0: N-1)*fs/N;  % 将fs个频率细分成fs*n个（即原来是[0, 1, 2, …, fs]，现在是[0, 1/N, 2/N, …, (N-1)*fs/N]）
t = (0: N-1)*T;  % 信号所持续的时长（N个周期）
nHz = 10;  % 画的频谱的横坐标到nHz
Hz = nHz*n;  % 画的频谱的横坐标的数组个数

x_ori = sin(2*pi*5*t)+0.7*sin(2*pi*2*t)+0.4*sin(2*pi*7*t-1);

2、加入噪声

Noise_White = [0.3*randn(1,length(t)/2), rand(1,length(t)/2)];  % 加入白噪声
x = x_ori + Noise_White;

3、绘制原始信号的时域、频域

figure
subplot(211),plot(x,'k'),title('原始信号时域'),xlabel('time [s]');  % 绘制原始信号时域
fx = abs(fft(x-mean(x)))/(N/2);  % 傅里叶变换
subplot(212),plot(f(1:Hz), fx(1:Hz),'k'),title('原始信号频域'),xlabel('frequency [Hz]');  % 绘制原始信号频域

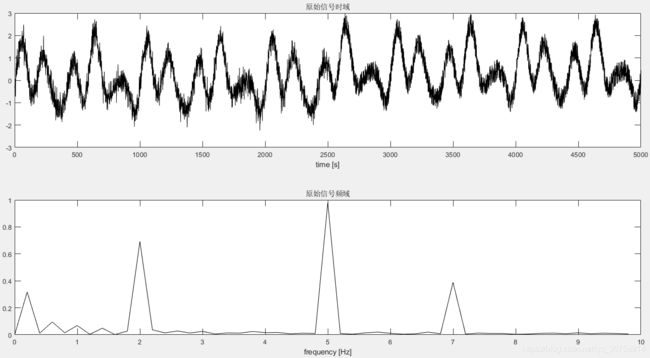由频域图可以看出该信号有三个主频率成分，分别为2Hz、5Hz以及7Hz。

4、滤波

4.1 移动平均滤波

b  =  [1 1 1 1 1 1]/6;
x1 = filter(b,1,x);

figure
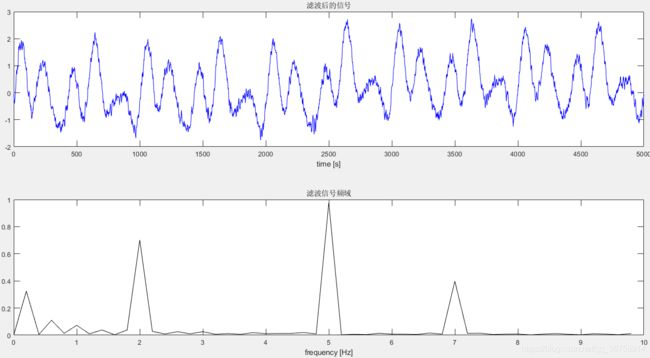
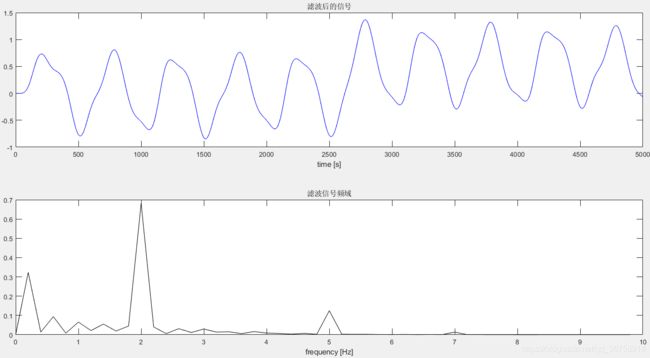
subplot(211),plot(x1,'b'),title('滤波后的信号'),xlabel('time [s]');
fx1 = abs(fft(x1-mean(x1)))/(N/2);  % 傅里叶变换
subplot(212),plot(f(1:Hz), fx1(1:Hz),'k'),title('滤波信号频域'),xlabel('frequency [Hz]');

4.2 中值滤波

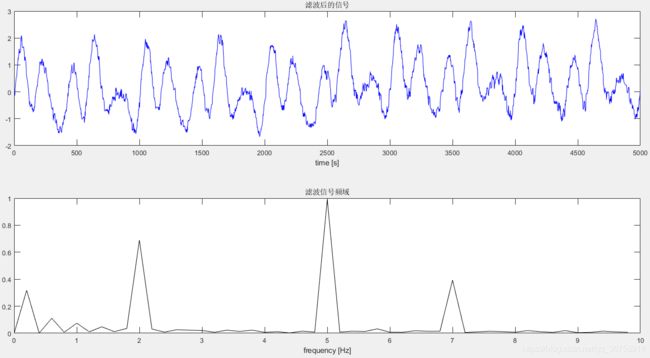
x1=medfilt1(x,10);

4.3 维纳滤波

Rxx=xcorr(x, x);              %得到混合信号的自相关函数
M=100;                                                             %维纳滤波器阶数
for i=1:M                                                           
    for j=1:M
        rxx(i,j)=Rxx(abs(j-i)+N);   %得到混合信号的自相关矩阵
    end
end
Rxy=xcorr(x,x_ori);       %得到混合信号和原信号的互相关函数
for i=1:M
    rxy(i)=Rxy(i+N-1);   %得到混合信号和原信号的互相关向量
end                                                                  
h = inv(rxx)*rxy';                                               %得到所要涉及的wiener滤波器系数
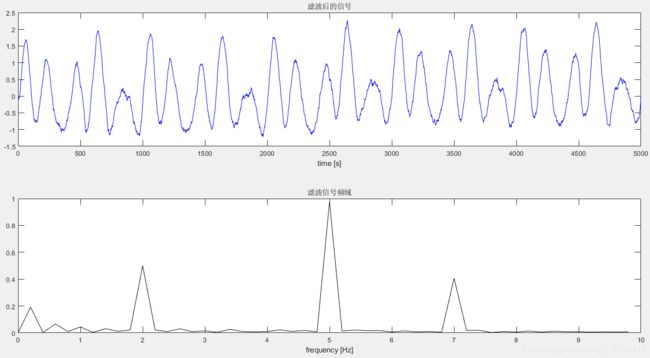
x1=filter(h,1, x);               %将输入信号通过维纳滤波器

4.4 自适应滤波

k=100;                                                  %时域抽头LMS算法滤波器阶数
u=0.001;                                             %步长因子

%设置初值
x1=zeros(1,N);                                  %output signal
x1(1:k)=x(1:k);                 %将输入信号SignalAddNoise的前k个值作为输出yn_1的前k个值
w=zeros(1,k);                                        %设置抽头加权初值
e=zeros(1,N);                                        %误差信号

%用LMS算法迭代滤波
for i=(k+1):N
        XN=x((i-k+1):(i));
        x1(i)=w*XN';
        e(i)=x_ori(i)-x1(i);
        w=w+2*u*e(i)*XN;
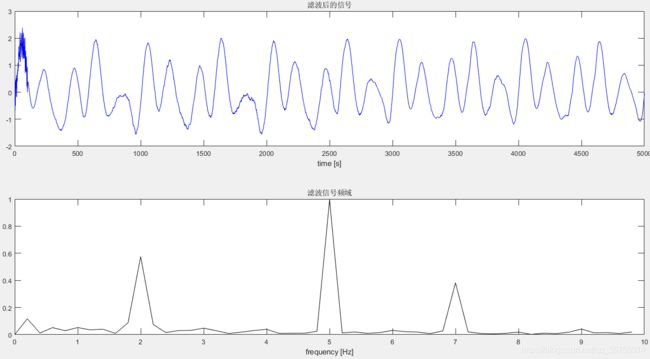
end

4.5 巴特沃斯滤波

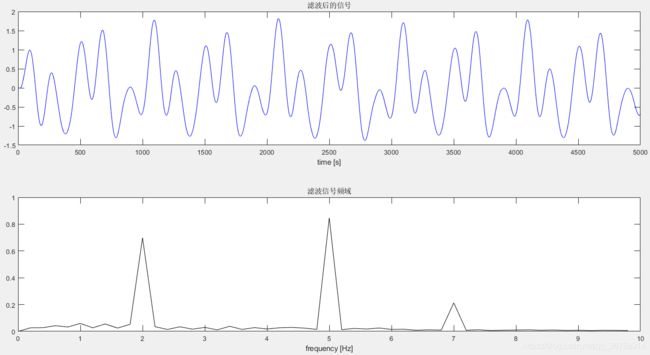
4.5.1 低通滤波

Wc=2*3/fs;                                          %截止频率 3Hz
[b,a]=butter(4,Wc,'low');  % 四阶的巴特沃斯低通滤波
x1=filter(b,a,x);

由图可见，3Hz以上的信号幅值明显降低。

4.5.2 高通滤波

Wc=2*3/fs;                                          %截止频率 3Hz
[b,a]=butter(4,Wc,'high');  % 四阶的巴特沃斯高通滤波
x1=filter(b,a,x);

由图可见，3Hz以下的信号幅值明显降低。

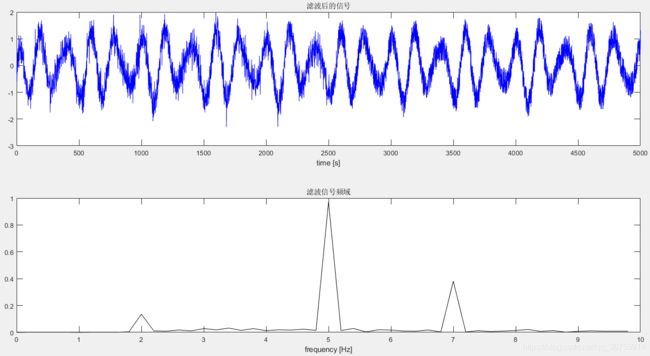
4.5.3 带通滤波

Wc1=2*1/fs;                                          %下截止频率 1Hz
Wc2=2*6/fs;                                          %上截止频率 6Hz
[b,a]=butter(2,[Wc1, Wc2],'bandpass');  % 二阶的巴特沃斯带通滤波
x1=filter(b,a,x);

由图可见，1Hz到6Hz以外的信号幅值明显降低。