信号与系统实验三 信号的卷积计算
目录
【实验目的】
【实验原理】(可选)
【实验设备】
【实验内容】
教材P103,T2-1(a)
1.对下图中的信号x1(t)=2u(t)-2u(t-1) ,x2(t)=u(t)-u(t-2),求y(t)=x1(t)*x2(t),并画出y(t)的波形图。
教材P104,T2-5(b)
2.序列x(n)与h(n)如下图所示,求x(n)* h(n),并绘图表示出来。
【实验感悟】
【实验目的】
(1)熟悉卷积的定义和表示。
(2)学会用MATLAB求连续时间信号和离散时间信号的卷积运算。
【实验原理】(可选)
卷积是一种重要的应用工具,是线性时不变系统对任意输入信号获取零状态响应的一种系统描述方法。卷积运算分为连续时间信号的卷积积分和离散时间信号的卷积和两种运算。
1.卷积积分
连续时间信号的卷积积分可以表示为:
2.卷积和
离散时间信号的卷积和可以表示为:
【实验设备】
(1)计算机。
(2)MATLAB软件。
【实验内容】
教材P103,T2-1(a)
1.对下图中的信号x1(t)=2u(t)-2u(t-1) ,x2(t)=u(t)-u(t-2),求y(t)=x1(t)*x2(t),并画出y(t)的波形图。
p=0.01;
t1=0:p:1;x1=ones(size(t1)); %size()命令求出矩阵的行数和列数,ones()生成全1阵;
t2=0:p:2;x2=ones(size(t2));
y=conv(x1,x2); %计算序列x1与x2的卷积和y
y=y*p;%缩小幅度
t0=t1(1)+t2(1); %计算序列y非零样值的起点位置
t3=length(x1)+length(x2)-2; %计算卷积和y的非零样值的宽度
t=t0:p:(t3*p+t0); %确定卷积和y非零样值的时间向量
subplot(2,2,1)
plot(t1,x1) %在子图1绘x1⑴时域波形图
title('x1')
xlabel('t')
ylabel('x1')
subplot(2,2,2)
plot(t2,x2) %在子图2绘x2 (t)时波形图
title('x2')
xlabel('t')
ylabel('x2')
subplot(2,2,3)
plot(t,y); %画卷积y(t)的时域波形
g=get(gca,'position'); %获取坐标轴的未知属性
g(3)=2.5*g(3);
set(gca,'position',g) %将第三个子图的横坐标范围扩为原来的2.5倍
title('y(t)=x1(t)*x2(t)')
xlabel('t')
ylabel('y(t)')
教材P104,T2-5(b)
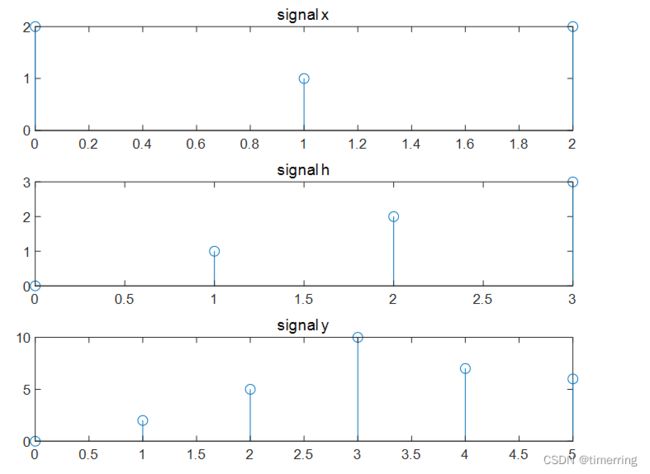
2.序列x(n)与h(n)如下图所示,求x(n)* h(n),并绘图表示出来。
n1 = 0:2;%设置自变量n1范围
n2 = 0:3;%设置自变量n2范围
n3 = 0:5;%设置自变量n3范围
x = [2,1,2];%给出序列X的对应取值
h = [0,1,2,3]; %给出序列h的对应取值
y = conv( x, h ); %求序列x和h的卷积和
subplot( 3,1,1 ); stem( n1,x ); title('signal x'); %作出离散序列x的图
subplot( 3,1,2 ); stem( n2,h ); title('signal h'); %作出离散序列h的图
subplot( 3,1,3 ); stem( n3,y ); title('signal y'); %作出离散序列y的图
【实验感悟】
通过本次实验,我学会了连续时间信号的卷积积分与离散时间信号的卷积和的matlab的实现方法,掌握了conv命令的用法:conv(u,v)返回向量u和v的卷积。如果u和v是多项式系数的向量,则对它们进行卷积相当于将两个多项式相乘。
在实验中,我也遇到了一些问题,在计算连续时间信号的卷积积分时,我没有将y乘一定的比例系数,导致得到的结果幅度很大,如下图所示:
从出来的结果可以看到,如果不乘以dT,那么所得结果会比原始数据大出很多倍。于是我将结果乘dT,即命令y=y*p,而做了这个乘法之后他们的幅度就相差无几了。
除此以外,在计算离散时间信号的卷积和时,我最初没有命令序列的起点,导致x1和x2的起点都是从1开始的,通过查阅官方文献得知,绘制离散信号时应提前规定序列的起点,即命令自变量的取值范围。