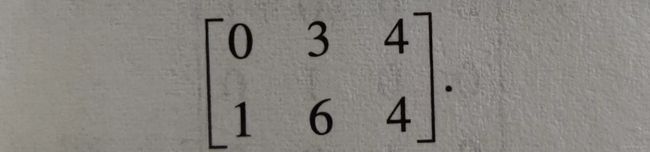【数学建模学习笔记【集训十天】之第七天】
数模学习目录
- Numpy 学习(续)
-
- 矩阵运算与线性代数
-
- 求范数
- 求解线性方程组的唯一解
- 求超定线性方程组的最小二乘解
- 求特殊值及特殊向量
-
- 运行结果如下:
- SciPy 学习(续)
-
- SciPy 优化器
-
- 查找 x + cos(x) 方程的根
-
- 运行 结果如下:
- 最小化函数
-
- x^2 + x + 2 使用 BFGS 的最小化函数
-
- 运行结果如下:
- SciPy Matlab 数组
-
- 导入 Matlab 格式数据
- Matplotlib 学习(续)
-
- Matplotlib 绘图线
-
- 线的类型
-
- 'dashed'【'--'】 破折线【运用】
-
- 运行效果如下:
- '-.'【dashdot】 点划线【运用】
-
- 运行效果如下:
- 线的颜色
-
-
- 运行效果如下:
- 运行效果如下:
- 运行效果如下:
-
- 线的宽度
-
-
- 运行效果如下:
-
- 多条线
-
-
- 运行效果如下:
-
- 更多线
-
-
- 运行效果如下:
-
- 上一章链接:[【数学建模学习笔记【集训十天】之第六天】](https://blog.csdn.net/m0_66318554/article/details/125570128)
-
- 每日一言:
-
- 持续更新中...
Numpy 学习(续)
矩阵运算与线性代数
# -*- coding = utf-8 -*-
# @Time : 2022/7/4 9:52
# @Author : lxw_pro
# @File : Numpy库学习-3.py
# @Software : PyCharm
# 矩阵运算与线性代数
# Python中的线性代数运算主要使用numpy.linalg模块,其常用函数如下:
'''
函数 说明
norm 求向量或矩阵的范数
inv 求矩阵的逆阵
pinv 求矩阵的广义逆阵
solve 求解线性方程组
det 求矩阵的行列式
lstsq 最小二乘法求解超定线性方程组
eig 求矩阵的特殊值和特殊向量
eigvals 求矩阵的特殊值
svd 矩阵的奇异值分解
qr 矩阵的QR分解
'''
# 范数计算
'''
计算范数的函数norm的调用格式:
norm(x, ord=None, axis=None, keepdims=False)
参数说明
参数 描述
x 表示要度量的向量或矩阵
ord 表示范数的种类,例如1范数、2范数等
axis: axis=0表示按列向量处理,求多个列向量的范数;
axis=1表示按行向量处理,求多个行向量的范数
axis=None表示矩阵范数
keepdims 是否保持矩阵的二维特性【True / False】
'''
求范数
题目描述
求下列矩阵的各个行向量的2范数,各个列向量的2范数和矩阵2范数
import numpy as np
jz = np.array([
[0, 3, 4],
[1, 6, 4]
]) # 矩阵
h = np.linalg.norm(jz, axis=1) # 求行向量2范数
l = np.linalg.norm(jz, axis=0) # 求列向量2范数
f = np.linalg.norm(jz) # 求矩阵2范数
print(f"行向量2范数为{np.round(h, 4)}")
# 运行结果为:行向量2范数为[5. 7.2801]
print(f"列向量2范数为{np.round(l, 4)}")
# 运行结果为:列向量2范数为[1. 6.7082 5.6569]
print(f"矩阵2范数为{round(f, 4)}")
# 运行结果为:矩阵2范数为8.8318
求解线性方程组的唯一解
import numpy as np
a = np.array([
[3, 1],
[1, 2]
])
b = np.array([9, 8])
# 解法1:
x = np.linalg.inv(a) @ b
print(x) # 输出 [2. 3.] 表示x=2, y=3
# 解法2:
x2 = np.linalg.solve(a, b)
print(x2) # 输出 [2. 3.] 表示x=2, y=3
求超定线性方程组的最小二乘解
import numpy as np
m = np.array([
[3, 1],
[1, 2],
[1, 1]
])
n = np.array([9, 8, 6])
x = np.linalg.pinv(m) @ n
print("最小二乘解为:{}".format(np.round(x, 4)))
# 运行结果为:最小二乘解为:[2. 3.1667]
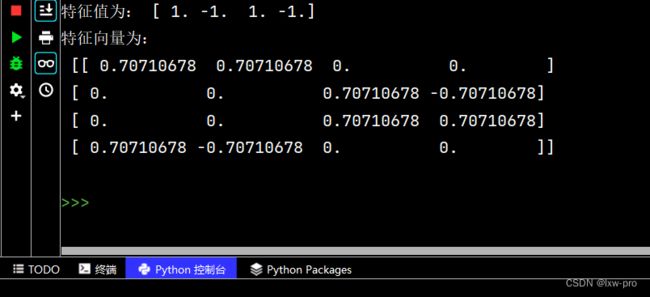
求特殊值及特殊向量
import numpy as np
q = np.eye(4)
w = np.rot90(q)
z, x = np.linalg.eig(w)
print("特征值为:", z) # 输出 特征值为: [ 1. -1. 1. -1.]
print("特征向量为:\n", x)
运行结果如下:
SciPy 学习(续)
SciPy 优化器
SciPy 的 optimize 模块提供了常用的最优化算法函数实现,我们可直接调用这些函数完成我们的优化问题
我们可以使用 SciPy 的 optimze.root 函数,这个函数需要两个参数:
- fun - 表示方程的函数
- x0 - 根的初始猜测
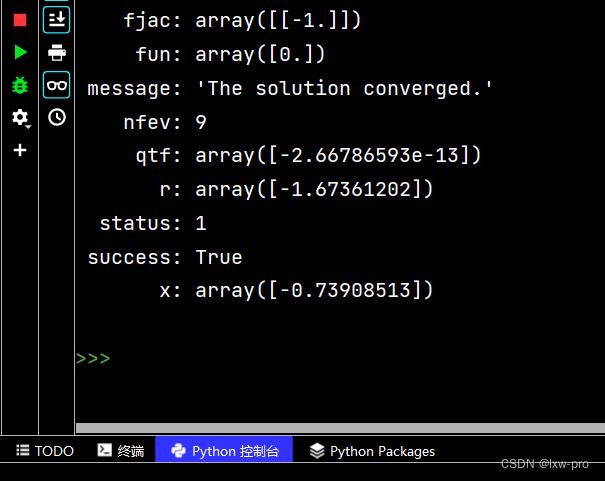
查找 x + cos(x) 方程的根
from scipy.optimize import root
from math import cos
def gen(x):
return x+cos(x)
myroot = root(gen, 0)
print(myroot.x) # 输出 [-0.73908513]
# 查看更多信息:
print(myroot)
运行 结果如下:
最小化函数
可以使用
scipy.optimize.minimize()函数来最小化函数
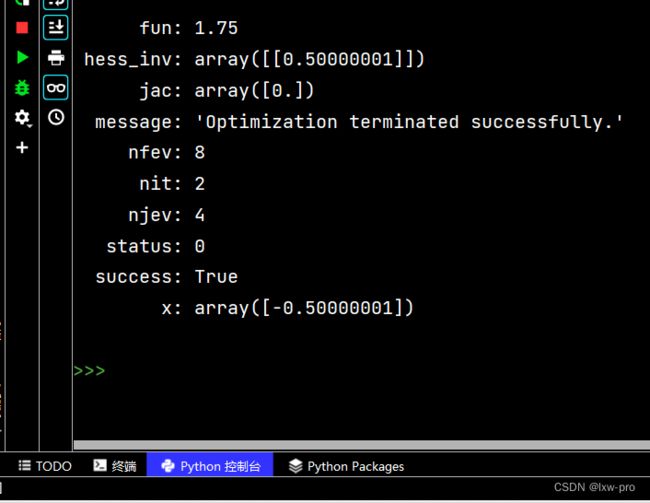
x^2 + x + 2 使用 BFGS 的最小化函数
'''
minimize() 函接受以下几个参数:
fun - 要优化的函数
x0 - 初始猜测值
method - 要使用的方法名称,值可以是:'CG','BFGS','Newton-CG','L-BFGS-B','TNC','COBYLA',,'SLSQP'。
callback - 每次优化迭代后调用的函数
options - 定义其他参数的字典
'''
# x^2 + x + 2 使用 BFGS 的最小化函数
from scipy.optimize import minimize
def zxh(x):
return x ** 2+x+2
mymin = minimize(zxh, 0, method='BFGS')
print(mymin)
运行结果如下:
SciPy Matlab 数组
NumPy 提供了 Python 可读格式的数据保存方法
'''
SciPy 提供了与 Matlab 的交互的方法
SciPy 的 scipy.io 模块提供了很多函数来处理 Matlab 的数组
以 Matlab 格式导出数据
savemat() 方法可以导出 Matlab 格式的数据。
'''
from scipy import io
import numpy as np
lxw = np.array([5, 2, 0, 1, 3, 1, 4])
io.savemat('lxw.mat', {'vec': lxw}) # 导出
# 注:上面的程序代码会生成一个mat文件
导入 Matlab 格式数据
loadmat() 方法可以导入 Matlab 格式数据
# 该方法参数:
# filename - 保存数据的文件名
from scipy import io
import numpy as np
lxw2 = np.array([6, 2, 9, 1, 4, 5])
io.savemat('lxw2.mat', {'vec': lxw2}) # 导出
mydata = io.loadmat('lxw2.mat') # 导入
print(mydata)
# 注:返回一个结构化数组,其键是变量名,对应的值是变量值
# 使用变量名 "vec" 可显示 matlab 数据的数组
print(mydata['vec']) # 输出 [[6 2 9 1 4 5]]
上面结果变成了二维,须squeeze_me利用降维
mydata2 = io.loadmat('lxw2.mat', squeeze_me=True)
print(mydata2['vec']) # 输出 [6 2 9 1 4 5]
Matplotlib 学习(续)
Matplotlib 绘图线
线的类型
‘dashed’【‘–’】 破折线【运用】
# Matplotlib 绘图线
# 线的类型
# 线的类型可以使用 linestyle 参数来定义【简写为 ls】
'''
类型 简写 说明
'solid' (默认) '-' 实线
'dotted' ':' 点虚线
'dashed' '--' 破折线
'dashdot' '-.' 点划线
'None' '' 或 ' ' 画线
'''
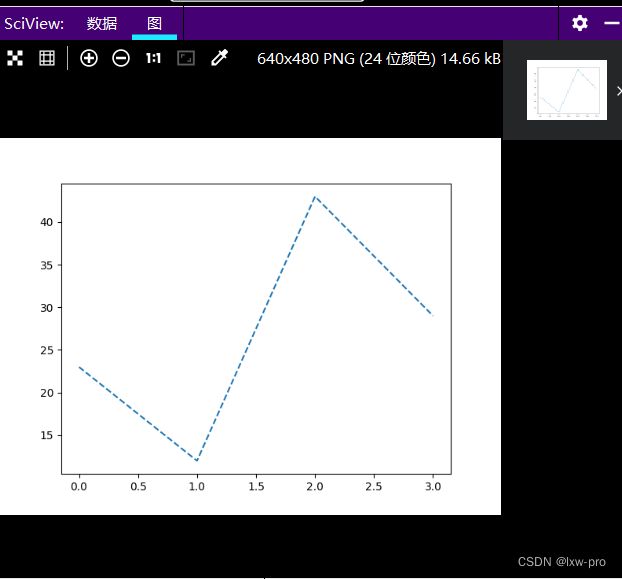
# 'dashed'【'--'】 破折线
import matplotlib.pyplot as plt
import numpy as np
lx = np.array([23, 12, 43, 29])
plt.plot(lx, linestyle='dashed')
plt.show()
运行效果如下:
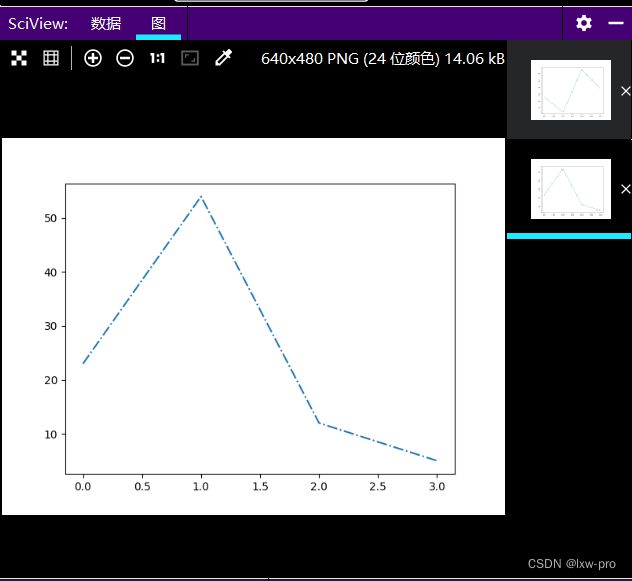
‘-.’【dashdot】 点划线【运用】
# 使用简写:
# '-.'【dashdot】 点划线
from matplotlib import pyplot as plt
import numpy as np
lx2 = np.array([23, 54, 12, 5])
plt.plot(lx2, ls='-.')
plt.show()
运行效果如下:
线的颜色
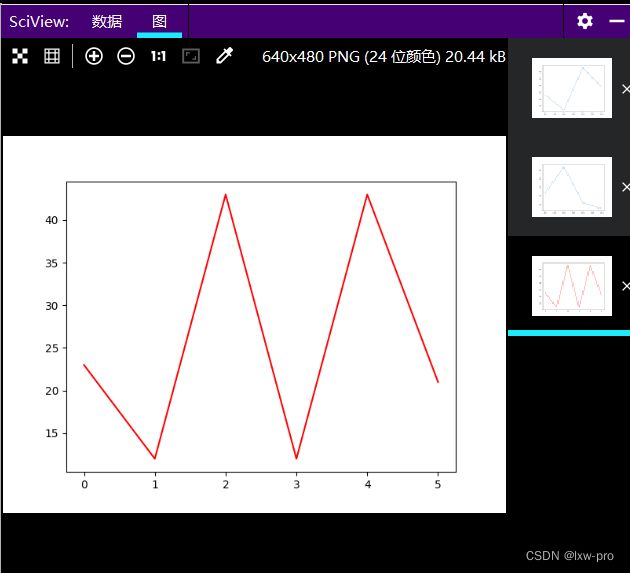
红色:
# 线的颜色
# 线的颜色可以使用 color 参数来定义,简写为 c
import matplotlib.pyplot as plt
import numpy as np
ys = np.array([23, 12, 43, 12, 43, 21])
plt.plot(ys, color='r')
plt.show()
运行效果如下:
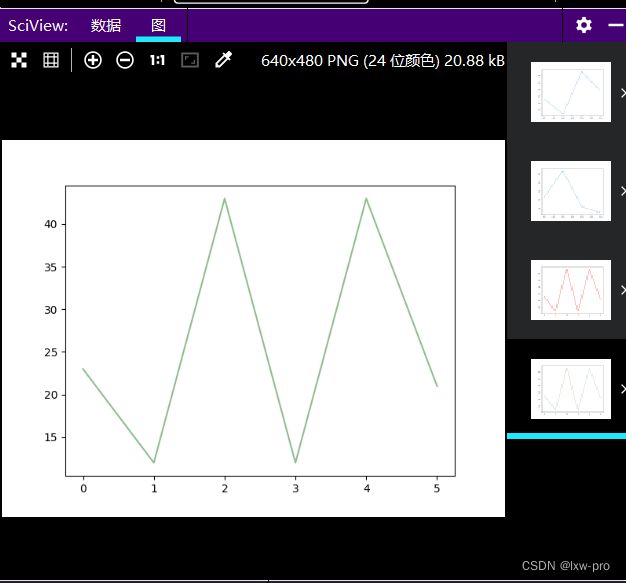
绿色
# 绿色
plt.plot(ys, c='#8FBC8F')
plt.show()
运行效果如下:
深绿色
# 深绿色
plt.plot(ys, c='SeaGreen')
plt.show()
运行效果如下:
线的宽度
# 线的宽度
# 线的宽度可以使用 linewidth 参数来定义,简写为 lw
import matplotlib.pyplot as plt
import numpy as np
kd = np.array([12, 23, 5, 12])
plt.plot(kd, linewidth='6.6')
plt.show()
运行效果如下:
多条线
# 多条线
# plot() 方法中可以包含多对 x,y 值来绘制多条线
import matplotlib.pyplot as plt
import numpy as np
d1 = np.array([12, 3, 23, 9])
d2 = np.array([6, 14, 8, 23])
plt.plot(d1)
plt.plot(d2)
plt.show()
运行效果如下:
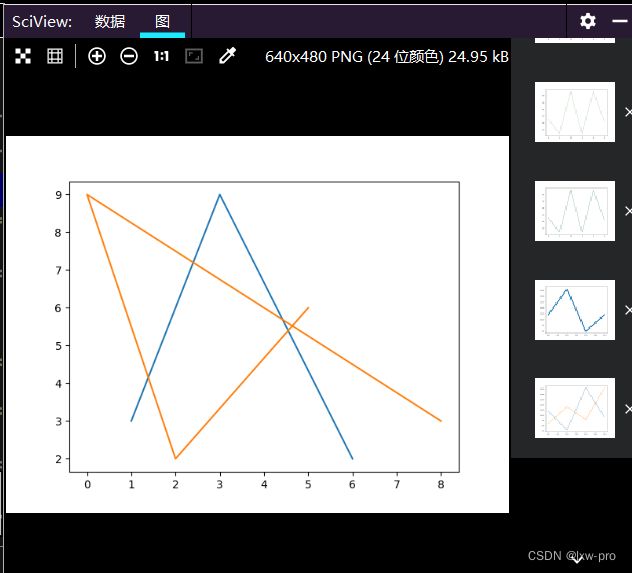
更多线
import matplotlib.pyplot as plt
import numpy as np
x1 = np.array([1, 2, 3, 6])
y1 = np.array([3, 6, 9, 2])
x2 = np.array([5, 2, 0, 8])
y2 = np.array([6, 2, 9, 3])
plt.plot(x1, y1, x2, y2)
plt.show()
运行效果如下:
上一章链接:【数学建模学习笔记【集训十天】之第六天】
每日一言:
有些往事只能回味,眼前的生活要向前看,不是所有的人或事都停留在一瞬,只有经历了才会明白这世界的规则或安定!