sklearn机器学习之SVM基础用法以及可视化
1.导入相应包
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
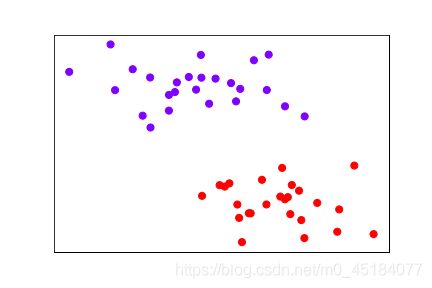
2.准备数据集并可视化
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.6)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='rainbow')
plt.xticks([])
plt.yticks([])
plt.savefig(r"C:\Users\86377\Desktop\1.png")
plt.show()
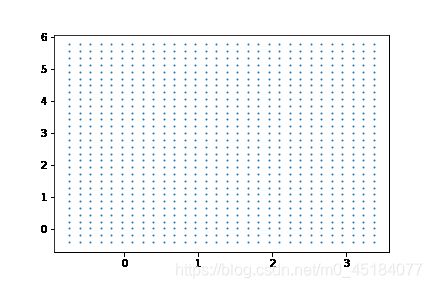
3.绘制点阵,查看距离
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#分割为30等份
axisx = np.linspace(xlim[0], xlim[1], 30)
axisy = np.linspace(ylim[0], ylim[1], 30)
#此函数较难,简单讲就是生成(xlim[0]:xlim[1], ylim[0]:ylim[1])的正方形区域点阵
axisy, axisx = np.meshgrid(axisy, axisx)
#ravel展平后堆叠
xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
#绘制点阵
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
4.建模并绘制超平面
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='rainbow')
plt.xticks([])
plt.yticks([])
ax = plt.gca()
clf = SVC(kernel='linear').fit(X, y)
Z = clf.decision_function(xy).reshape(axisx.shape)
#画三条等高线,分别是Z为-1,Z为0和Z为1的三条线,Z为对应axisx,axisy对应点的距离,此函数为绘制距离为-1, 0, 1的点组成的线,linestyles为样式
ax.contour(axisx, axisy, Z, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
绘制图像如下:

-1表示当超平面平移时最近的点,距离范围为【-1,1】
5.将绘制图像包装成函数
#将绘图包装成函数
def plot_svc_decision_function(model, ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
axisx = np.linspace(xlim[0], xlim[1], 30)
axisy = np.linspace(ylim[0], ylim[1], 30)
#axisy, axisx = np.meshgrid(axisy, axisx)
axisx, axisy = np.meshgrid(axisx, axisy)
xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
p = model.decision_function(xy).reshape(axisx.shape)
ax.contour(axisx, axisy, p, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
6.SVC中的内置属性
clf.predict(X)
clf.score(X, y)
clf.support_vectors_
clf.n_support_
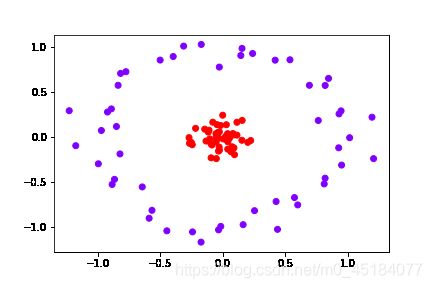
7.生成环形数据集
from sklearn.datasets import make_circles
#noise为增加噪声
X, y = make_circles(100, factor=0.1, noise=0.1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='rainbow')
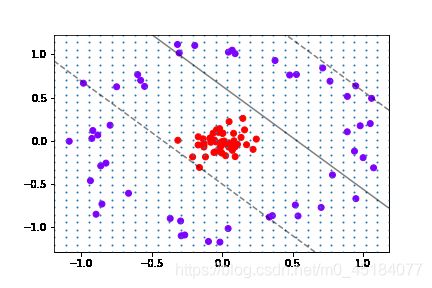
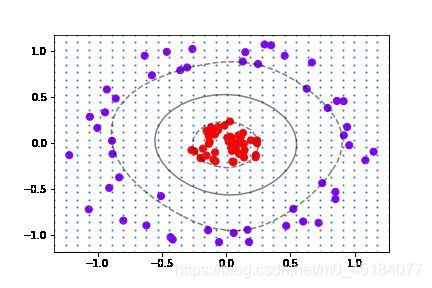
8.建模并可视化查看效果
clf = SVC(kernel='linear').fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='rainbow')
plot_svc_decision_function(clf)
9.为非线性函数增维
#生成新的一列
r = np.exp(-(X ** 2).sum(1))
rlim = np.linspace(min(r), max(r), 100)
from mpl_toolkits import mplot3d
#定义绘制函数
def plot3D(elev=30, azim=30, X=X, y=y):
ax = plt.subplot(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='rainbow')
ax.view_init(elev=elev, azim=azim)
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
plt.show()
plot3D()
绘制图像如下:
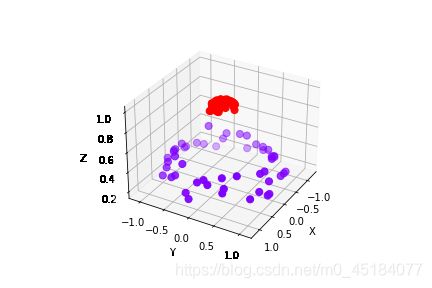
通过公式将原本二维数据投影到三维空间,此时三维空间可以被一个超平面分隔开。
10.使用’rbf’内置核函数
#设置为rbf核
clf = SVC(kernel='rbf').fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='rainbow', s=50)
plot_svc_decision_function(clf)