【论文阅读】CVPR2021——SCF-Net:Learning Spatial Contextual Feature for Large-Scale Point Cloud Segmentation

【论文】

1. Abstract

近年来，如何从大规模点云中学习有效特征进行语义分割越来越受到关注。针对这一问题，本文提出了一种可学习的模块，从大规模点云中学习空间上下文特征(Spatial Contextual Features)，称为SCF。所提出的模块主要由三个块组成，包括局部极坐标表示块、双距离注意力池化块和全局上下文特征块(the local polar representation block, the dual-distance attentive pooling block, and the global contextual feature block.)。对于每个3D点，首先探索局部极坐标表示块，以构建对z轴旋转不变的局部空间表示，然后设计双距离注意力池化块，以利用其邻居的表示，根据它们之间的几何和特征距离来学习更具区别性的局部特征，最后设计全局上下文特征块，以利用其空间位置和邻域与全局点云的体积比来学习每个3D点的全局上下文。所提出的SCF模块可以很容易地嵌入到用于点云分割的各种网络架构中，自然地产生了具有编码器-解码器架构的新的3D语义分割网络，在本工作中称为SCF-Net。在两个公共数据集上的大量实验结果表明，所提出的SCF-Net在大多数情况下比几种最先进的方法表现得更好。

2. Introduction

最近，一些为大规模点云设计的方法被提出，如SPG、PCT和RandLA-Net。然而，他们中的大多数仍然不得不面对以下问题：如何从大规模点云中学习更有效的特征进行语义分割？

受上下文信息在许多视觉任务中的成功的启发，我们研究了如何从大规模点云中学习空间上下文特征以进行语义分割。我们将上述问题分解为三个子问题：

1. 如何表示三维点的局部上下文？
2. 如何学习局部上下文特征？
3. 如何学习全局上下文特征？

分别提出三个模块解决，见摘要。

主要贡献如下：

• （1）我们提出了the Local Polar Representation (LPR) block，它可以学习每个三维点的局部z轴旋转变化表示。（类似RandLA-Net的Local Spatial Encoding (LocSE) 模块，都是对点坐标的增强，学习到几何的局部上下文。）
• （2）我们提出了the Dual-Distance Attentive Pooling (DDAP) block，它可以基于几何距离和特征距离自动学习有效的局部特征。（类似RandLA-Net的Attentive Pooling模块，都是对点特征的增强并聚合，学习到特征的局部上下文，只不过本文在学习注意力得分矩阵时多考虑了双距离（几何距离和特征距离）。）
• （3）我们提出了the Global Contextual Feature (GCF) block，它可以从点云中学习每个三维点的全局上下文。（相比于RandLA-Net ，增加了全局信息。）
• （4）我们提出了SCF模块，它可以应用于各种体系结构，用于探索新的点云分割网络。第4节中的大量实验结果表明，通过将SCF模块嵌入到标准的编码器-解码器架构中，所提出的SCF-Net实现了最先进的性能。

3. Related work

与基于投影和离散化的方法不同，基于点的方法直接处理点云。这些方法通常可分为点卷积和逐点MLP方法。逐点MLP方法使用共享MLP作为基本单位。这些方法的开创性工作，PointNet，学习了每点的特点。但是，每个点的特征无法捕捉局部几何模式，点之间的上下文信息会丢失。为了解决这个问题，最近已经探索了许多方法，这些方法主要利用两种技术，包括邻域特征池化和基于注意力的聚合(neighboring feature pooling and attention-based aggregation) (还有graph networks and RNN (Recurrent Neural Networks))。

4. Method

在这一部分中，我们首先提出了用于大规模点云分割的SCF模块，该模块由三个模块组成：LPR、DDAP和GCF。然后我们介绍SCFNet，它有一个带有SCF模块的编码器-解码器。

4.1 SCF Module

4.1.1 Local Polar Representation

目的：注意，在许多真实场景中，属于同一类别的对象的方向通常是不同的，例如会议室中的椅子，这表明直接从输入3D点学习的特征是方向敏感的。这种对方向敏感的情况会在一定程度上妨碍分割性能。为了解决这个问题，我们提出了学习z轴旋转不变表示的LPR，它表示极坐标系统而不是笛卡尔坐标系中的3D点的局部上下文。LPR的架构如图2所示。

如图2所示，局部空间信息（三维点坐标）被输入到LPR块，输出是局部极坐标表示和几何距离。

LPR包括以下步骤：
(1)Constructing initial local representation: 首先，计算极坐标系统中相邻点的相对坐标。通过基于欧几里德距离的KNN算法收集 {p_i¹, p_i²,…, p_i^k,…, p_i^K} ，local representation表示为 (dis_i^k, Φ_i^k, θ_i^k) ：



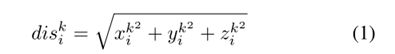
其中 (x_i^k, y_i^k, z_i^k) 是笛卡尔坐标系中的相对坐标。

(2)Calculating the local direction: 我们计算局部邻域的质心(center-of-mass)点 p_i^m，局部方向被定义为从 p_i 到 p_i^m ，其具有以下两个优点：

• a)质心点能反映局部邻域的全貌；
• b)通过在 p_i^m 的计算中使用平均值，可以有效地减少下采样引入的随机性。

(3) Updating the Φ_i^k and θ_i^k: 被更新为：


在LPR块之后，局部表示对于z轴旋转不变。

4.1.2 Dual-Distance Attentive Pooling

目的：给定local representation，下一个要面对的问题是如何利用邻近点特征学习局部上下文特征。启发式地，距离是衡量点之间相关性的重要变量。距离越小，它们就越相关。因此，我们提出了双距离注意力池化块，通过集成邻近点特征 {f_i¹, f_i²,…, f_i^k,…, f_i^K} ，来自动学习有效的局部上下文特征。DDAP的架构如图4所示。

如图4所示，DDAP有三个输入，包括几何距离、点特征和几何模式。为了生成几何模式，LPR输出的局部极坐标表示与绝对坐标连接，并通过共享的MLP进一步处理。

我们关注两个代表性的距离，即在世界空间中的几何距离和在特征空间中的特征距离（但邻域依旧是欧式空间中的邻域，而不是特征空间中的邻域，只是计算了特征距离而已）。g(i) 和 g(k) 是DDAP块的输入特征向量，feature distance为：

两种距离的负指数被用来学习attentive pooling weights。此外，我们使用 λ 来调整 d_if^k 以处理其不稳定性，因为点特征是由网络自动学习的：


attentive pooling weights：

最后，通过用学习到的权重计算相邻点特征的加权和来获得局部上下文特征：

4.1.3 Global Contextual Feature

目的：局部上下文特征描述了邻域中点之间的上下文，但它对语义分割的区分度不够。为了获得更有效的特征，我们提出了全局上下文特征块来从三维点学习全局上下文。GCF的图示如图5所示。

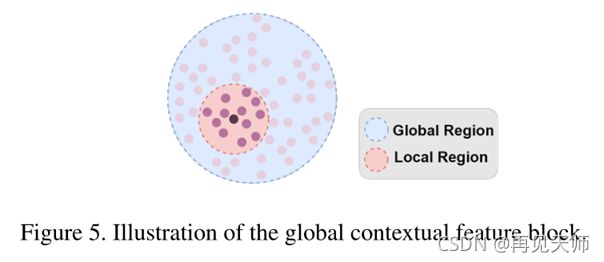
我们在全局上下文表示中使用位置和体积比 r_i 。需要注意的是，同一类别的物体(如椅子)在不同场景下通常有不同的风格，它们的几何架构一般相似，但不完全相同。因此，考虑到体积比对局部和全局边界球内的内部点的位置不敏感，我们使用它以便表示可以容忍相同类别的对象的轻微几何变形。

其中，v_i 是对应 p_i 的邻域边界球的体积，v_g 是点云边界球的体积。

x-y-z坐标用于表示局部邻域的位置。因此，全局上下文特征被定义为：

4.1.4 Architecture of SCF

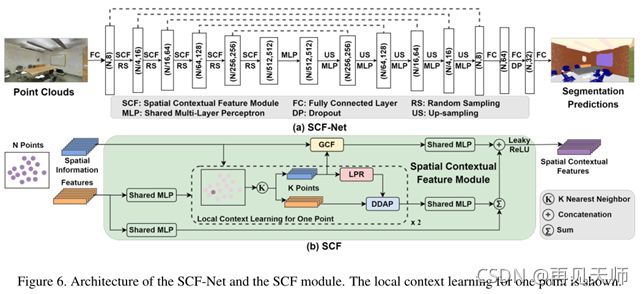
SCF模块的架构如图6(b)所示。它的输入是空间信息（三维点坐标）和先前学习的特征。空间信息用于学习局部和全局上下文特征，而学习的特征仅用于局部特征学习。LPR和DDAP块学习局部上下文特征。图6(b)显示了一个点的局部上下文特征学习，该学习并行应用于每个点。

由LPR构建的局部上下文表示由DDAP自动整合。我们学习局部上下文特征（点坐标增强和点特征注意力聚合）两次（整体*2），以增加上下文信息。然后，将这些特征进一步添加到另一个特征图中（与输入点特征残差连接），从而生成局部特征。

全局上下文特征由GCF块从空间信息中学习。

该模块的输出是学习的空间上下文特征，它是局部和全局上下文特征的拼接。

4.2 Architecture of SCF-Net

在这一小节中，我们将所提出的SCF模块嵌入到标准的编码器-解码器架构中，从而产生了新的分割网络SCF-Net。SCF-Net的完整架构如图6(a)所示。

如图6(a)所示，网络的输入是大小为N×d的点云，其中N是点数，d是输入特征维数。每点特征首先由FC层提取，维数统一为8。五个编码器层被逐步用于编码特征。其中，随机采样用于点云降采样，嵌入SCF模块学习空间上下文特征。点数从N逐渐减少到N/512，特征维数从8增加到512。接下来，五个解码器层用于解码特征。通过最近邻插值对编码特征进行上采样，该插值简单地利用最近邻处的值作为插值，并通过跳跃连接与中间特征图进一步拼接。最后，使用三个连续的FC层来预测语义标签。输出是大小为N×c的分割预测，其中c是类别的数量。此外，交叉熵损失用于训练。

5. Experiments

S3DIS是一个大规模的室内点云数据集，由包括271个房间的6个区域的点云组成。每个点云都是一个中等大小的房间，每个点都用13个类中的一个语义标签进行标注。

Semantic3D是一个大规模的室外点云数据集，有超过30亿个来自现实世界的点，包括城市和乡村场景。它由15个训练点云和15个在线测试点云组成。除了坐标和颜色信息，每个点也有强度值，但我们不使用它们。每个点都用8个类中的一个语义标签来标注。

5.1 Evaluation on S3DIS

5.2 Evaluation on Semantic3D

5.3 Ablation Study

在S3DIS和Semantic3D上的实验结果验证了该方法的有效性。为了更好地理解网络，我们进一步评估它，并进行以下两组实验。由于Semantic3D测试集缺乏公开的基础事实，实验是在S3DIS上进行的。

5.3.1 Ablation Study on SCF

以下消融研究旨在研究三个提议块的影响。我们使用标准的6倍交叉验证来评估消融网络，并在表3中显示了比较结果。（就是与RandLA-Net的比较。）

首先，我们移除GCF块。从第二行到第一行的改进表明全局上下文特征的引入可以有效提高对场景的理解。

其次，我们还用一个正常的自注意力池化(SAP)来替换DDAP块。在学习注意力聚合权重时，仅考虑邻近点特征。第三排验证了DDAP的有效性， mIoU提高了1.2%。

最后，我们用正常的局部空间表示(LSR)替换LPR块。LPR的取代降低了1.4%的分割性能，这表明了它的影响。距离信息在LPR和LSR都被明确编码。它们之间的主要区别是相对位置的表示方法。在LSR，它以笛卡尔坐标表示，而在LPR，它被表示为相对于局部方向的相对角度，对围绕z轴的旋转不敏感。这一改善证实了局部表示的重要性。

5.3.2 Ablation Study on DDAP

进行以下消融研究是为了了解DDAP做出的各种设计选择的影响。

首先，我们研究距离的影响。本研究中的所有消融网络都在S3DIS的区域2进行评估，根据mIoU结果，该区域是最困难的区域。我们依次移除特征距离和几何距离，并在表4中报告比较结果。特征距离的去除使分割性能降低了0.4%，而几何距离的去除导致了1.5%的下降。由此，证明了双距离的有效性。此外，可以看出受益于几何距离的提升更大，这也说明了关注空间上下文特征的重要性。

其次，探索了 双距离d_i^k 和 特征f_i^k 的不同融合方法（生成 d_i^k+ ），并在区域2进行了实验。我们评估了两种典型的融合方法，拼接和加权求和，并在表5中报告了比较结果。对于加权求和，考虑三个权重比。实验结果表明，拼接法优于加权求和法。比例为5:5的加权求和是三者中最好的，证明了 d_i^k 和 f_i^k 的有效性。

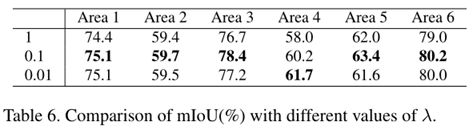
最后，我们评估λ的三个值。实验在6个区域进行，以研究总体效果，表6报告了比较。可以看出，0.1（因为受益于几何距离的提升更大）是一个更好的选择，它在六个领域中的五个领域上实现了最佳性能。