【算法合集】前缀和与差分

 哈喽~大家好呀，感谢大家的支持，这篇我们来看看前缀和与差分

 个人主页：个人主页​​​​​             

 系列专栏：【算法系列】    

与这篇相关的文章：            

【算法合集】深搜广搜Prim与Kruskal	【算法合集】深搜广搜Prim与Kruskal_程序猿追的博客-CSDN博客
【算法合集】关于数论	【算法合集】关于数论_程序猿追的博客-CSDN博客
【算法合集】高精度问题	【算法合集】高精度问题_程序猿追的博客-CSDN博客

目录

一、前缀和

1、一维前缀和

2、二维前缀和

二、差分

1、一维差分

2、二维差分

---

一、前缀和

1、一维前缀和

啥是前缀和？

字面意思前面数到后面数的和（又叫区间和），假设我们有一组数组[1,2,3,4,5]，输入左区间与右区间，这区间它们两的和（不是下标哟）。

例子

数组长度为 6 ，元素是[1,2,3,4,5,6]，区间 1 到 3 的和是6，这样的就叫一维前缀和。

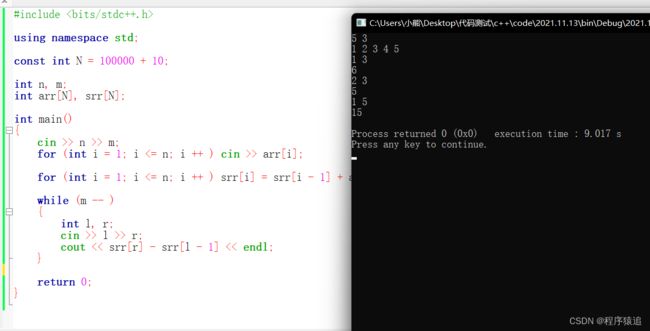
直接看代码

#include 

using namespace std;

const int N = 100000 + 10;

int n, m;
int arr[N], srr[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> arr[i];

    for (int i = 1; i <= n; i ++ ) srr[i] = srr[i - 1] + arr[i];

    while (m -- )
    {
        int l, r;
        cin >> l >> r;
        cout << srr[r] - srr[l - 1] << endl;
    }

    return 0;
}

n 是数组的长度，m 是要操作的次数，l 是左区间，r是右区间

2、二维前缀和

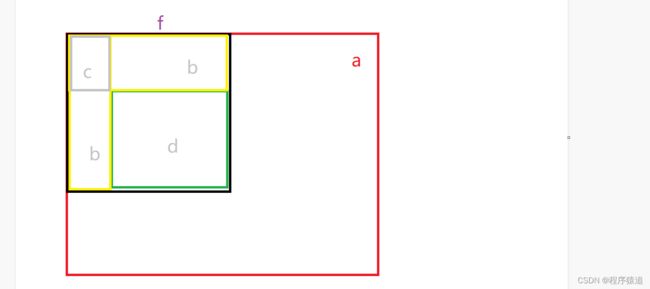
 啥是二维前缀和？

我们直接看图

假设 a 是个大区间的我们要求 d 区间的数据和，先求 f 的和再减去两个 b 区间的和，b 区间明显多减了一次，所以左后面再加上 c 区间。

假设有一个长度为 5 宽度为 3 的一个数组，里面都是1,2,3数据，坐标（1,1）到（2,2）的和明显是 1 + 2 + 1 + 2。

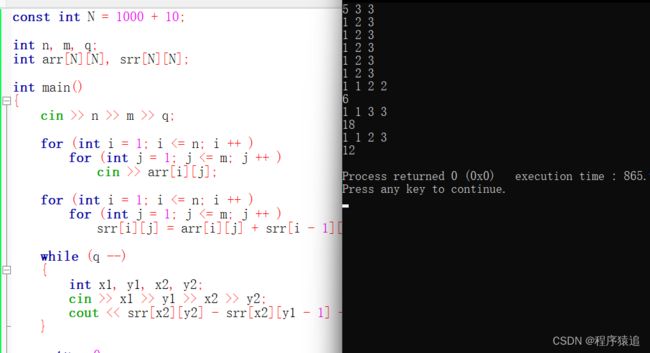
#include 

using namespace std;

const int N = 1000 + 10;

int n, m, q;
int arr[N][N], srr[N][N];

int main()
{
    cin >> n >> m >> q;

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            cin >> arr[i][j];

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            srr[i][j] = arr[i][j] + srr[i - 1][j] + srr[i][j - 1] - srr[i - 1][j - 1];

    while (q --)
    {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << srr[x2][y2] - srr[x2][y1 - 1] - srr[x1 - 1][y2] + srr[x1 - 1][y1 - 1] << endl;
    }

    return 0;
}

二、差分

1、一维差分

通过上面我们知道了，什么是前缀和，那么什么是差分呢？就是在一区间减去某一个数或加上某一个数，假如 1 到 3 区间有1,2,3 三个数据，对它进行 + 1 与 - 2操作，再来求它的和，这就是典型的差分。

#include 

using namespace std;

const int N = 100000 + 10;

int n, m, arr[N], srr[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
    {
        cin >> arr[i];
        srr[i] += arr[i];
        srr[i + 1] -= arr[i];
    }

    while(m --)
    {
        int l, r, c;
        cin >> l >> r >> c;
        srr[l] += c;
        srr[r + 1] -= c;
    }
    for(int i = 1; i <= n; i ++)
    {
        srr[i] += srr[i - 1];
        cout << srr[i] << ' ';
    }
}

2、二维差分

同样的道理这里就不多说了。

#include 

using namespace std;

const int N = 1010;

int n, m, q;
int arr[N][N], srr[N][N];

int main()
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &srr[i][j]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            arr[i][j] = srr[i][j] - srr[i - 1][j] - srr[i][j - 1] + srr[i - 1][j - 1];

    while (q --)
    {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        arr[x1][y1] += c;
        arr[x1][y2 + 1] -= c;
        arr[x2 + 1][y1] -= c;
        arr[x2 + 1][y2 + 1] += c;
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            srr[i][j] = arr[i][j] + srr[i - 1][j] + srr[i][j - 1] - srr[i - 1][j - 1];

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ ) printf("%d ", srr[i][j]);
        cout << endl;
    }

    return 0;
}

 （求关注）持续更新中……