数据结构 二叉树是什么?看完这篇你就知道了(包含二叉树面试题详解)
系列文章目录
文章目录
- 系列文章目录
- 一、二叉树的概念
-
- 1.1为什么会存在树结构?
- 1.2树的基本概念
- 1.3辨别树与非树
- 二、二叉树
-
- 2.1概念
- 2.2二叉树重要性质(笔试常考选择题)
- 2.3常见二叉树
-
- 满二叉树
- 练习:辨别下列图中是不是完全二叉树
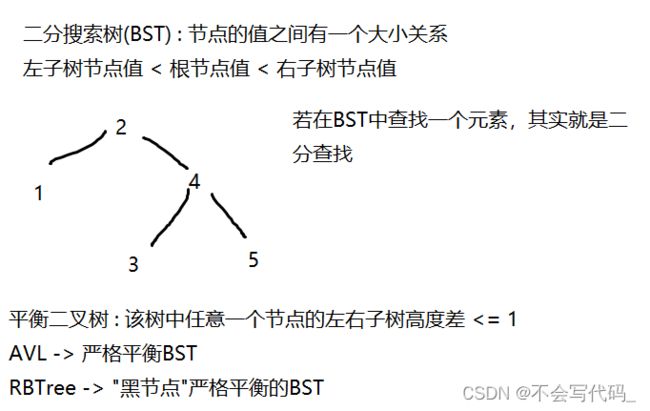
- 二分搜索树
- 2.4完全二叉树编号问题(考点)
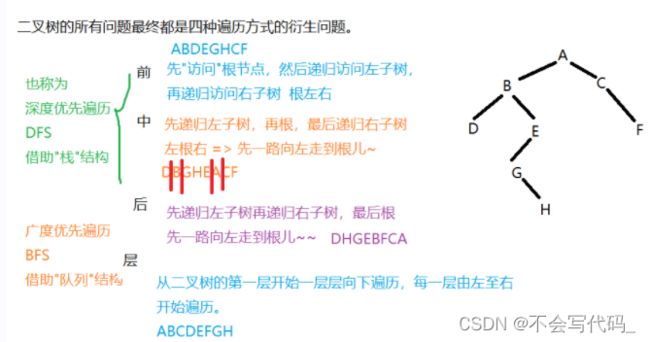
- 2.5二叉树遍历问题(递归)
-
- 三中遍历方式特点总结(刷题用的上)
- 2.6二叉树的遍历问题(迭代)
-
- 1.前序遍历
- 2.中序遍历
- 3.后序遍历
- 2.7二叉树常用方法(都是遍历衍生问题)
-
- 1.计算二叉树中节点个数
- 2.统计一颗二叉树叶节点(度为0的节点)的个数
- 3.求当前二叉树第k层节点个数(重点掌握)
- 4.求当前二叉树的高度
- 5.判断当前二叉树是否包含val值
- 6.二叉树的层序遍历(借助队列)
- 练习:层序遍历统计二叉树节点个数
- 三、常见面试题(简单)
-
- 3.1 leetcode 144号问题
- 3.2 leetcode100 判断两颗二叉树是否相同(重点)
- 3.3 leetcode572 是否包含subTree(重点)
- 3.4 leetcode110 平衡二叉树的判断(重点)
- 3.5 leetcode101 对称二叉树
- 四、常见面试题(中等+困难)
-
- 4.1 leetcode958 二叉树的完全性检验
- 4.2 leetcode236 寻找公共祖先
- 4.3 nowCoder根据前序遍历与中序遍历构造二叉树
-
-
- ACM编程模式
-
- 4.4 leetcode105前序与中序遍历构造二叉树
-
- 中序遍历的特点
- 4.5 leetcode106中序和后序遍历结果构建二叉树
-
- 4.3和4.4两个问题总结(重点)
- 4.6nowCoder JZ36二分搜索树与双向链表
- 4.7二叉树创建字符串
一、二叉树的概念
1.1为什么会存在树结构?
1.2树的基本概念
线性数据结构——线性表,元素之间逻辑上一个挨着一个,呈直线排列数组,链表,栈,队列,字符串
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
1.有一个特殊的节点,称为根节点,根节点没有前驱节点
2.除根节点外,其余节点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm,其中每一个集合 Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根节点有且只有一个前驱,可以有0个或多个后继
3.树是递归定义的。
第三点中x=n-1是因为根节点没有父节点,所以比节点个数少一个

1.3辨别树与非树
二、二叉树
2.1概念
2.2二叉树重要性质(笔试常考选择题)

注意事项:重点记忆第三点(数据结构必考)
推导过程:
一:二叉树中只存在三种情况的节点,一种是一个子树n1,一种是两个子树n2,还有一种没有子树的n0。三种类型节点相加之后等于总结点个数n。
二:边和节点存在关系x=n-1,只有一个子树的有一条边,两个子树的有两条边,n1+2n2=n-1这是边长关系
两式相减就得出点三条结论:度为0的节点一定比度为2的节点多一个

2.3常见二叉树
满二叉树
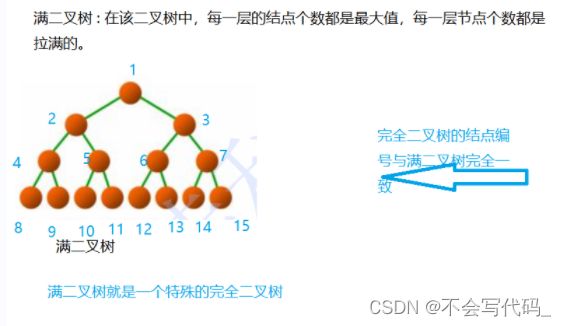
区分是不是完全二叉树的关键点:完全二叉树节点编号与满二叉树是否完全一致,并且完全二叉树只能是在最深层不满,其它层数的节点都是满的。
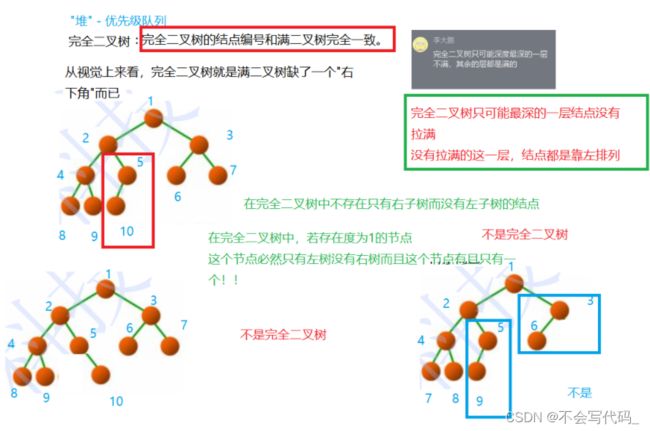
练习:辨别下列图中是不是完全二叉树
不是,因为编号与满二叉树节点编号不一致。也不满足只能最深层节点数不满,图中第二层的节点数不满,关键点就是编号看是否一致。
二分搜索树
2.4完全二叉树编号问题(考点)
2.5二叉树遍历问题(递归)
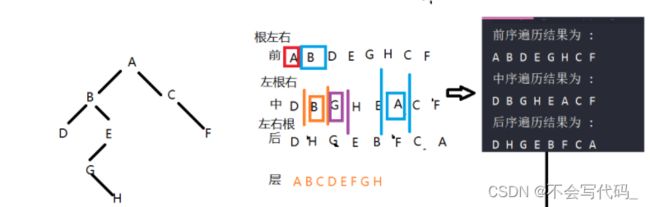
关于"序"可以理解为访问输出根节点的次序,前就是第一次遇到就输出,以此类推。
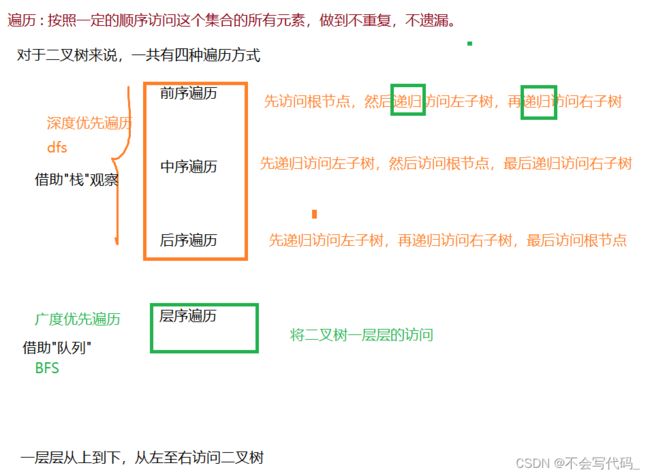
前序遍历:根 左 右
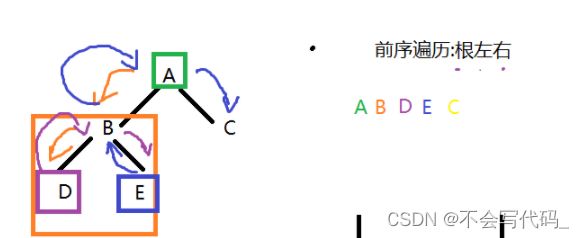
中序遍历:左 根 右
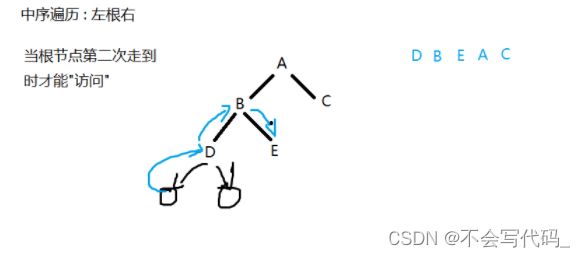
后序遍历:左 右 根
层序遍历:从左往右,从上到下

三中遍历方式特点总结(刷题用的上)
/*
* 二叉树基本操作
* */
class TreeNode<E>{
//当前节点的值
E val;
//左子树的根
TreeNode<E> left;
//右子树的根
TreeNode<E> right;
public TreeNode(E val) {
this.val = val;
}
}
public class MyBinTree<E> {
public TreeNode<Character> root;
// 建立一个测试二叉树
public void build() {
TreeNode<Character> node = new TreeNode<>('A');
TreeNode<Character> node1 = new TreeNode<>('B');
TreeNode<Character> node2 = new TreeNode<>('C');
TreeNode<Character> node3 = new TreeNode<>('D');
TreeNode<Character> node4 = new TreeNode<>('E');
TreeNode<Character> node5 = new TreeNode<>('F');
TreeNode<Character> node6 = new TreeNode<>('G');
TreeNode<Character> node7 = new TreeNode<>('H');
node.left = node1;
node.right = node2;
node1.left = node3;
node1.right = node4;
node4.left = node6;
node6.right = node7;
node2.right = node5;
root = node;
}
代码示例:掌握递归本质
/**
* 传入一颗二叉树根节点root。按照前序遍历根左右方式进行输出
* */
public void preOrder(TreeNode root){
if(root==null){
return;
}
//打印根
System.out.print(root.val+" ");
//左子树
preOrder(root.left);
//右子树
preOrder(root.right);
}
/**
* 传入一颗二叉树的根节点root。就能按照中序遍历左根右的方式进行输出
* @param root
*/
public void inOrder(TreeNode root) {
if (root == null) {
return;
}
// 先打印左子树,交给子函数
inOrder(root.left);
// 打印根
System.out.print(root.val + " ");
// 最后打印右子树
inOrder(root.right);
}
/**
* 传入一颗二叉树的根节点root。就能按照后序遍历左右根的方式进行输出
* @param root
*/
public void postOrder(TreeNode root) {
if (root == null) {
return;
}
// 先打印左子树,交给子函数
postOrder(root.left);
// 再打印右子树
postOrder(root.right);
// 最后打印根
System.out.print(root.val + " ");
}
}
2.6二叉树的遍历问题(迭代)
1.前序遍历
易错点:深度优先是借助栈的数据结构,所以压栈时,如果节点左右子节点都不为空应该先压右节点,在下次循环时就可以先弹出左节点。
public List<Integer> preOrder(TreeNode root){
List<Integer> ret=new ArrayList<>();
if(root==null){
return ret;
}
Deque<TreeNode> stack=new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()){
//先访问根节点
TreeNode cur= stack.pop();
ret.add(cur.val);
//将右子树先压入栈中
if(cur.right!=null){
stack.push(cur.right);
}
//再处理左子树
if(cur.left!=null){
stack.push(cur.left);
}
}
return ret;
}
}
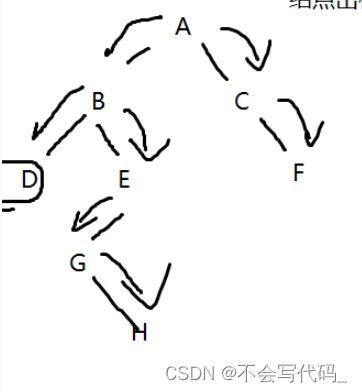
2.中序遍历
核心思路:左根右,先一路向左走到底,碰到第一个左子树为空的根节点出栈
public List<Integer> inorderTraversal(TreeNode root){
List<Integer> ret=new ArrayList<>();
if(root==null){
return ret;
}
Deque<TreeNode> stack=new ArrayDeque<>();
TreeNode cur=root;
//以下两个条件一个不满足都不可以停止循环
while(cur!=null||!stack.isEmpty()){
//先一路向左走到底
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
//cur已经为空,弹出栈顶元素,遇到第一个左子树为空的节点
cur= stack.pop();
ret.add(cur.val);
//继续访问右子树
cur=cur.right;
}
return ret;
}
}
总结:1.第一个大的while加上cur!=null的原因是此时根节点不入栈,但栈是空的,所以表示循环还没有结束。但是cur=cur.right可能出现空节点,此时cur=null但是栈不等于空,所以他俩只要一个条件不满足循环都还要继续。
2.一开始根节点不能先入栈,要一路走到底。
3.内层while循环就是为了一路向左子树走到底
3.后序遍历
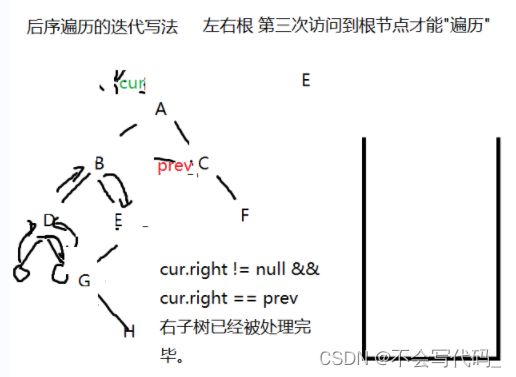
难点:如何判断右树也走完了?

完全访问结束的节点:例如图中的prev先置为null,因为一开始一个元素也没有处理过,当cur位于D时,左右子树都为空,此时D元素弹出栈,prev就等于D节点。

public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ret=new ArrayList<>();
if(root==null){
return ret;
}
TreeNode cur=root;
Deque<TreeNode> stack=new ArrayDeque<>();
//上一个被完全处理的节点,左右子树都已经被访问完毕
//最开始肯定一个都没处理,所以为空
TreeNode prev=null;
while(cur!=null||!stack.isEmpty()){
//1.一路向左走到底
while(cur!=null){
stack.push(cur);
cur=cur.left;
}
//2.查看栈顶元素
cur=stack.pop();
if(cur.right==null||cur.right==prev){
ret.add(cur.val);
prev=cur;
cur=null;
}else{
stack.push(cur);
cur=cur.right;
}
}
return ret;
}
}
易错点:1.cur在处理过后一定要置空,否则又会进入while循环,还是刚刚处理过的节点,变成死循环
2.7二叉树常用方法(都是遍历衍生问题)
1.计算二叉树中节点个数
/**
*传入一颗以root为根节点的二叉树,就能求出结点个数为多少
* */
public int getNodes(TreeNode root){
//边界
if(root==null){
return 0;
}
//此时根节点不为空,根节点至少都有一个
//至于根节点的左右子树还有有多少个节点
//我们根据语义,把剩下节点数交给子方法去处理
//总的节点个数=根节点+左子树所有节点+右子树所有节点
return 1+getNodes(root.left)+getNodes(root.right);
//最简洁的代码 三目运算符
//return root==null?0:1+getNodes(root.left)+getNodes(root.right);
}
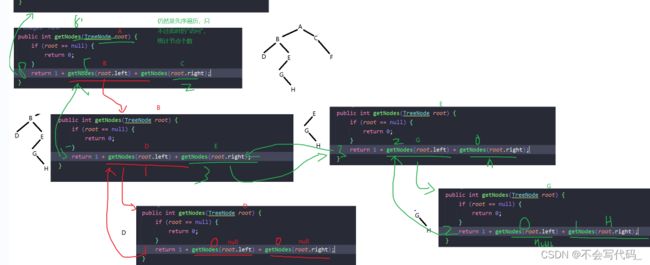
递归展开图:
首先传入A节点,A节点不为空,走到return语句,分别传入左节点B和有节点C进入子方法,并且节点个数+1。再看B节点传入下一个子方法,左右节点D,E不为空,同理走到return方法,并把B节点的左右节点传入,节点个数+1。当把D节点传入子方法时,它的左右节点都为null,所以传入子方法后返回值为0。其他节点以此类推。
2.统计一颗二叉树叶节点(度为0的节点)的个数
/**
* 传入一颗以root为根节点的二叉树,就能求出所有叶子结点
* */
public int getLeafNodes(TreeNode root){
//边界,空树
if(root==null){
return 0;
}
//边界,只有一个根节点
//走到这说明存在根节点
if(root.left==null&&root.right==null){
return 1;
}
//root不为空并且左右不为空,root肯定不是叶子节点
//根绝语义剩下的节点计算只能交给子方法
//总叶子结点=左树中叶子结点个数+右树中叶子节点个数
return getLeafNodes(root.left)+getLeafNodes(root.right);
}
3.求当前二叉树第k层节点个数(重点掌握)
核心思路:拆分问题,比如当k=3时,我们在A节点思考问题就是求第三层节点个数,同时可以转化为A的左树在B节点求B树的第二层节点数加上A的右树C节点求第二层节点个数

/**
* 传入一颗以root为根的二叉树,计算出第k层节点个数,k在取值范围内
* */
public int getKLevelNodes(TreeNode root,int k){
//边界,空树和k不合法
if(root==null||k<=0){
return 0;
}
//边界,根节点只有一层
if(k==1){
return 1;
}
//拆分问题
//求以root为根的第k层节点个数=root.left为根第k-1层个数
//加上以root.right为根的k-1层个数
return getKLevelNodes(root.left,k-1)+getKLevelNodes(root.right,k-1);
}
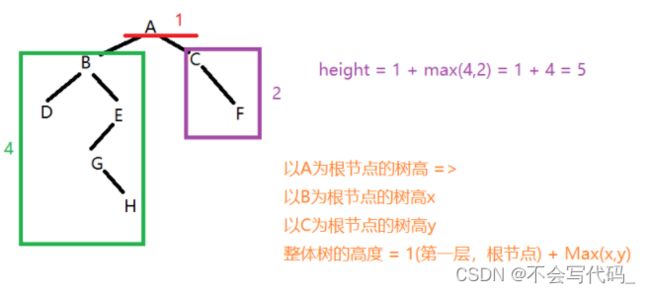
4.求当前二叉树的高度
核心思想:拆分问题,拆成1(根节点高度)+左右子树为根节点的树高最大值
/**
* 传入一颗以root为根的二叉树,计算出树的高度
* */
public int height(TreeNode root){
//边界
if(root==null){
return 0;
}
//1就是当前树的树根所在第一层
//树高=根节点第一层+max(左子树树高,右子树树高)
return 1+Math.max(height(root.left),height(root.right));
}
5.判断当前二叉树是否包含val值
注意事项:泛型中的比较需要借助equals方法。
/**
* 传入一颗以root为根的二叉树,判断是否包含val
* */
public boolean contains(TreeNode root,E val){
//边界
if(root==null){
return false;
}
//当前树根的值和传入值相等
//注意泛型使用equals方法进行比较
if(root.val.equals(val)){
return true;
}
//继续在左子树或者右子树找val
//只要有一个子树有就可以,不能是&&
return contains(root.left,val)||contains(root.right,val);
}
6.二叉树的层序遍历(借助队列)
/**
* 借助队列,实现二叉树的层序遍历
* */
public void levelOrder(TreeNode<E> root){
Deque<TreeNode<E>> queue=new LinkedList<>();
queue.offer(root);
//循环终止条件就是队列为空
while(!queue.isEmpty()){
//取出当前层的节点个数,每当进行下一层遍历时
//队列中就存储了该层的所有元素
int n=queue.size();
for (int i = 0; i < n; i++) {
TreeNode<E> node=queue.poll();
System.out.print(node.val+" ");
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
}
}
练习:层序遍历统计二叉树节点个数
/**
* 使用层序遍历统计一颗二叉树的节点个数
* */
public int getNodesNonRecursion(TreeNode root){
if(root==null){
return 0;
}
int size=0;
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int n=queue.size();
for (int i = 0; i < n; i++) {
TreeNode node=queue.poll();
//出队一个,计数器加一
size++;
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
}
return size;
}
三、常见面试题(简单)
3.1 leetcode 144号问题
两个易错点:
1.返回值是个List的集合,每遍历一个元素就把这个元素加入到集合中,不是简单的ruturn输出
2.new这个集合应该在方法外部,否则递归每次产生一个新的集合就只会返回根节点。(下图反映的就是这个问题,错误示例,集合中只会有根节点)
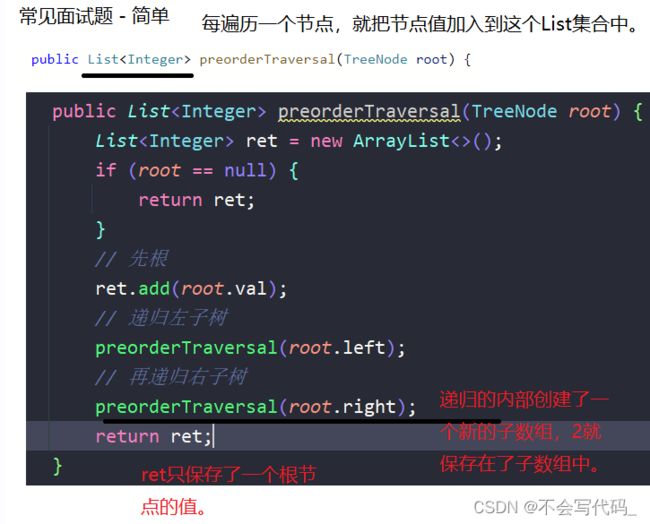
我们必须把每个节点保存在一个集合中,因此集合的声明不可以放在递归函数内部
//不可以在循环内部创建数组
List<Integer> ret=new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if (root == null) {
return ret;
}
//先根
ret.add(root.val);
//递归左子树
preorderTraversal(root.left);
//递归右子树
preorderTraversal(root.right);
return ret;
}
}
3.2 leetcode100 判断两颗二叉树是否相同(重点)
添加链接描述

核心思路:还是要根据语义来写递归。比如这道题方法:给一个根节点然后判断这棵树是否相同,那我们就先处理根节点,然后根节点的左右子树就交给子方法处理。
 还有一个易错点需要注意:一定要先写&&的关系,如果先写||的关系,两个都为空的节点也会走||的关系,此时就会把都为null的节点判断为false。
还有一个易错点需要注意:一定要先写&&的关系,如果先写||的关系,两个都为空的节点也会走||的关系,此时就会把都为null的节点判断为false。
public boolean isSameTree(TreeNode p, TreeNode q) {
//1.边界,有一个树为空就不相同
if(p==null&&q==null){
return true;
}
//边界,两棵树都为空肯定相同
if(p==null||q==null){
return false;
}
//根据语义,根节点相同,再用子方法去解决左右节点为根节点的子树是否相同
return p.val==q.val&&isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}
}
3.3 leetcode572 是否包含subTree(重点)
添加链接描述

注意事项:为何要用100号问题辅助解决?是因为此题根据语义只能判断是否包含subRoot,可能根节点就是我们要找的子树
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
//边界都为空肯定相同
if(root==null&&subRoot==null){
return true;
}
//边界有一个树为空肯定不相同
if(root==null||subRoot==null){
return false;
}
//剩下三种情况判断是否包含
//第一种情况就是用到100号问题的方法,用根节点判断两棵树是否相同
//第二种情况就是把root左子树交给子方法判断是否包含subTree
//注意:subRoot是不变的
//第三种同理
return isSameTree(root,subRoot)||isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot);
}
public boolean isSameTree(TreeNode p, TreeNode q) {
//1.边界,有一个树为空就不相同
if(p==null&&q==null){
return true;
}
//边界,两棵树都为空肯定相同
if(p==null||q==null){
return false;
}
//根据语义,根节点相同,再用子方法去解决左右节点为根节点的子树是否相同
return p.val==q.val&&isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}
}
3.4 leetcode110 平衡二叉树的判断(重点)
添加链接描述

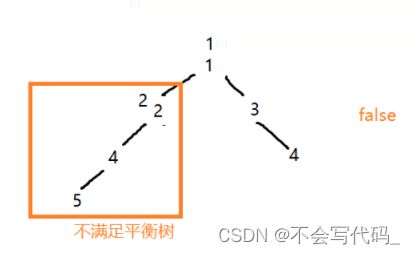
核心思路:一个树是否满足,先看根节点是否满足,通过求深度的方法,再求以根节点左右为子树的深度,再通过求绝对值方法比较出两个节点相差高度,如果根节点满足平衡二叉树之后,根节点的左右子树交给子方法去处理。
public boolean isBalanced(TreeNode root) {
//边界
if(root==null){
return true;
}
//计算根节点左树高度
int left=height(root.left);
//计算根节点右树高度
int right=height(root.right);
//计算绝对值
int abs=Math.abs(right-left);
return abs<=1&&isBalanced(root.left)&&isBalanced(root.right);
}
//计算高度的方法
public int height(TreeNode root){
if(root==null){
return 0;
}
return 1+Math.max(height(root.left),height(root.right));
}
}
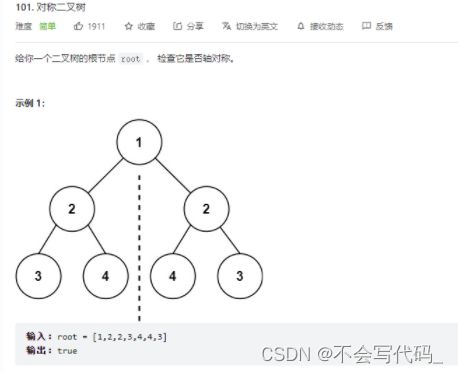
3.5 leetcode101 对称二叉树
添加链接描述
边界条件:空树是一切的树!!!!!用来作为边界条件
此时会发现一个方法不够用,原方法只能传入一个根节点判断是否是镜像树,所以此时还要引用一个方法来判断左右子树是否对称
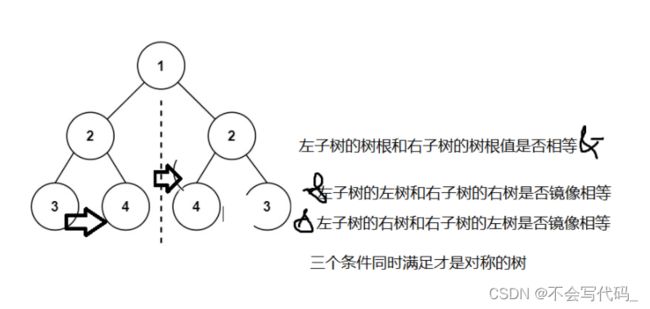
/**
* 传入一个节点判断是否是镜像树
* @author hide_on_bush
* @date 2022/5/14
*/
public class Num101_IsSymmetric {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
}
//传入两个根节点,判断两个树是否镜像是相等的
return isMirror(root.left, root.right);
}
/**
*传入一颗树的树根t1和t2,就能判断这两棵树是否镜像
* t1.val==t2.val
* */
private boolean isMirror(TreeNode t1, TreeNode t2) {
//边界 空树是一切的树
if (t1 == null && t2 == null) {
return true;
}
if (t1 == null || t2 == null) {
return false;
}
return t1.val==t2.val&&isMirror(t1.left,t2.right)&&isMirror(t1.right,t2.left);
}
}
注意和100号sameTree问题的区别:
sameTree是结构和数值完全相同,相同的结构的树不一定是对称的树。
Mirror结构一定是相同的,但是数值不一定相同

使用二叉树的层序遍历解决:
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
}
Deque<TreeNode> queue = new LinkedList<>();
queue.offer(root.left);
queue.offer(root.right);
while (!queue.isEmpty()) {
//每次都必须两个元素同时入队,同时出队
TreeNode t1 = queue.poll();
TreeNode t2 = queue.poll();
//可能有空节点入队
if (t1 == null && t2 == null) {
continue;
}
//找反例
if (t1 == null || t2 == null) {
return false;
}
if(t1.val!=t2.val){
return false;
}
//继续入队,对称入队
queue.offer(t1.left);
queue.offer(t2.right);
//继续入队
queue.offer(t1.right);
queue.offer(t2.left);
}
return true;
}
}
四、常见面试题(中等+困难)
4.1 leetcode958 二叉树的完全性检验
添加链接描述
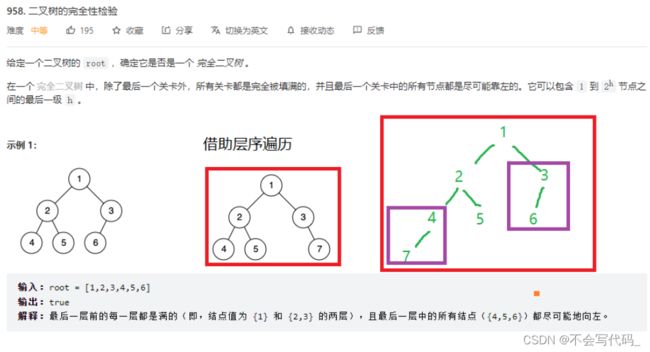
核心思想:首先要理解什么是完全二叉树(2.3中有阐述)

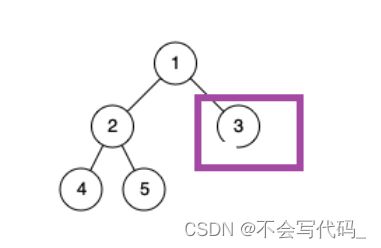
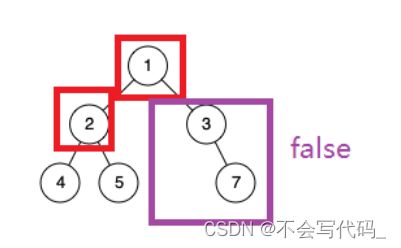
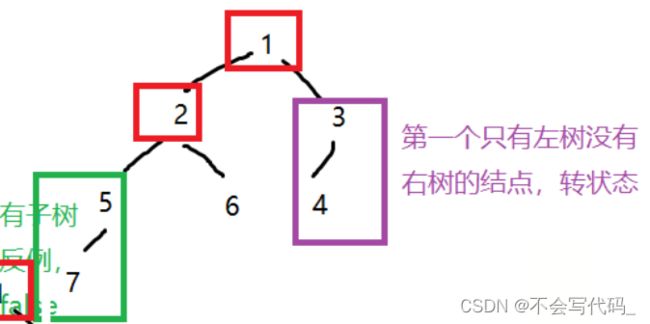
例如上图:首先位于第一阶段,遍历了1和2节点,当遍历到3节点时,就切换状态,变为第二阶段。

找反例:
总结:
1.掌握标志位的使用
2.找反例的方法
3.题目中说明节点个数是1——100所以不用判空
4.易错点:容易忽略遇到叶子节点也要转阶段的情况

public boolean isCompleteTree(TreeNode root) {
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
//判断是否是第二阶段
boolean isSecondStep=false;
//层序循环终点
while(!queue.isEmpty()){
//进入第一阶段
TreeNode cur=queue.poll();
if(!isSecondStep){
//第一个阶段必须所有节点都有左右子树
if(cur.left!=null&&cur.right!=null){
//都符合第一阶段,入队左右子树
queue.offer(cur.left);
queue.offer(cur.right);
}else if(cur.left!=null){
//此时遇到只有左子树没有右子树的节点,进入第二阶段
isSecondStep=true;
queue.offer(cur.left);
}else if(cur.right!=null){
//只有右树没有左树,找到反例
return false;
}else{
//还有一种情况转阶段就是碰到叶子节点
//可以画图看看,易错点
//左树空,右树也空
isSecondStep=true;
}
}else{
//上面if分支所有语句结束
//此时处在第二阶段,所有节点都必须为叶子节点
if(cur.left!=null||cur.right!=null){
//不是叶子节点,反例
return false;
}
}
}
//遍历完所有节点还没找到反例,就说明是完全二叉树
return true;
}
}
4.2 leetcode236 寻找公共祖先
添加链接描述

核心思路:
1.首先要弄清什么是最近公共祖先,并且确定使用什么方法去遍历。(如上图示例)
2.画图找技巧,例如当p=6,q=7时。

3.通过大量画图可以确定,如果一个节点是p和q的lca,那么p和q只可能出现在3个位置,第一种情况:p和q其中一个在lca,另一个在lca左子树;第二种情况:p和q其中一个在lca,另一个在lca右子树;第三种情况:p和q都不在lca,p和q分别在lca的左右子树中;

4.以上三步就确定了我们写代码的边界条件:


板书5_15有递归展开图
/**
* 寻找最近公共祖先
* @author hide_on_bush
* @date 2022/5/16
*/
public class Num236_Lca {
//最近公共祖先
private TreeNode lca;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//丛树中每个节点开始遍历找p,q
findNode(root, p, q);
return lca;
}
/**
* 以当前根节点出发,能否找到p或者q,找到一个return true
* */
private boolean findNode(TreeNode root, TreeNode p, TreeNode q) {
if(root==null){
return false;
}
//返回1时说明左子树中找到一个节点
int left=findNode(root.left,p,q)?1:0;
//返回1时说明右子树中找到一个节点
int right=findNode(root.right,p,q)?1:0;
//根节点就是p或者q中的一个
int mid=(root==p||root==q)?1:0;
if(left+right+mid==2){
//此时p和q出现在以root为根的两个位置,这个root一定是lca
lca=root;
}
//大于0只找到一个节点
return (left+mid+right)>0;
}
}
4.3 nowCoder根据前序遍历与中序遍历构造二叉树
ACM编程模式
白板编程,就是给你了一张大白纸,此时所有的方法,类定义,输入输出都需要我们自己来实现。

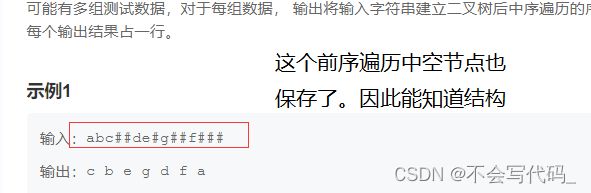
还需要注意一些细节,例如下题:
1.需要多次输入
2.输出的每个结果都需要打上空格
3.输入输出各占一行


解析:输入的是先序遍历,输出的是中序遍历,先序遍历是根左右。
画出树的结构: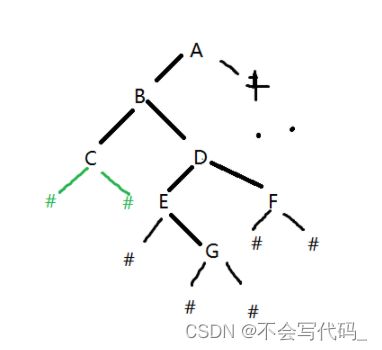
根据图写出中序遍历的结果:对比题目中输出结果一致,说明还原的是正确的。
![]()
递归展开图在5_15的板书
import java.util.Scanner;
/**
* ACM编程模式
* @author hide_on_bush
* @date 2022/5/17
*/
/**
* 根节点定义
* */
class TreeNode{
//题目要求数据类型是字符
char val;
TreeNode left;
TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}
public class KY11_BuildTree {
//先序遍历处理到第几个字符
private static int index=0;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
//题目要求多次输入
while (scanner.hasNextLine()) {
//接收多组输入
String str = scanner.nextLine();
//题目要求,根据字符串建立二叉树,并返回根节点
TreeNode root=preOrderBuild(str);
//题目要去输出该二叉树中序遍历的结果
inOrder(root);
//输出一个结果换行
System.out.println();
//继续读取下一个字符串
index=0;
}
}
/**
* 二叉树的中序遍历
* */
private static void inOrder(TreeNode root) {
if(root==null){
return;
}
//左
inOrder(root.left);
//根
System.out.print(root.val+" ");
//右
inOrder(root.right);
}
/**
* 根据传入的字符串str,按照先序遍历方式还原二叉树,返回二叉树根节点
* */
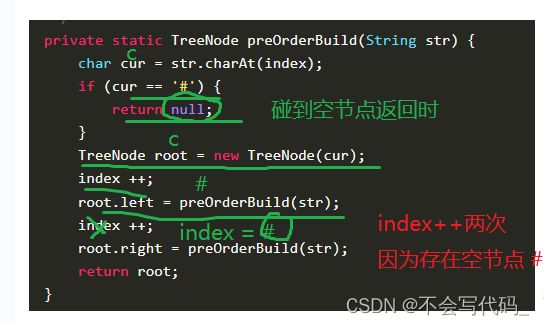
private static TreeNode preOrderBuild(String str) {
//读取字符串第一个字符
//abc##de#g##f###
char cur=str.charAt(index);
if(cur=='#'){
//空树,无需创造节点
return null;
}
//题目要求创建二叉树
//首先要先创建这个根节点
TreeNode root=new TreeNode(cur);
//第一个字符处理完要处理下一个
index++;
//根据语义,第一个字符之后的字符串交给子方法处理(构建左子树)
root.left=preOrderBuild(str);
//处理了第一个和第二个字符,剩下的交给子方法(构建右子树)
index++;
root.right=preOrderBuild(str);
return root;
}
}
4.4 leetcode105前序与中序遍历构造二叉树
添加链接描述

先思考一个问题:只给其中一种遍历方式,不给空节点,能否确定一棵树?
答案肯定是不行的。会有好几种情况

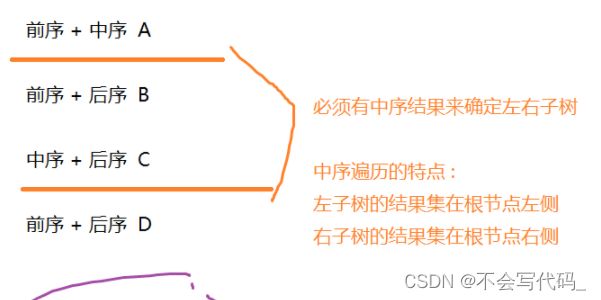
中序遍历的特点
BST:二分搜索树
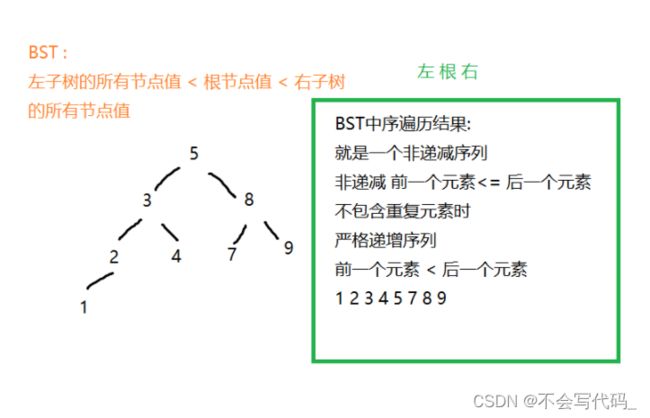
根据前序遍历和中序遍历特点(下图解释),用题目中例子模拟画图找规律:图中前序遍历的"3"一定是这棵树的根节点,再从中序遍历中得知,“9"一定在根节点"3"的左树,“15 20 7"在右树。” 9"这个数字通过中序遍历观察,左右都为空,所以9是个叶子结点。再通过前序访问到"20”,根据前序知道它是右树的根节点,再根据中序遍历结果发现’‘20’'是右子树根节点。剩下画法以此类推。


递归展开图在5_15板书中
/**
* 表示当前处理到先序遍历结果的第几个节点
*/
private int index = 0;
public TreeNode buildTree(int[] preorder, int[] inorder) {
//不用判空
return builderTreeHelper(preorder,inorder,0,inorder.length-1);
}
/**
* 从前序遍历中取出根节点,借助中序遍历[left...right)还原二叉树,返回树根的根节点
* */
private TreeNode builderTreeHelper(int[] preorder, int[] inorder, int left, int right) {
//边界条件
//空区间
if(left>right){
return null;
}
//边界:前序遍历中根节点已经全部访问结束。没有新节点
if(index==preorder.length){
return null;
}
//从前序遍历中取出根节点
TreeNode root=new TreeNode(preorder[index]);
//遍历下一次要处理的根节点
index++;
//从前序遍历得到的根节点在中序遍历中的索引位置
int pos=find(root.val,inorder);
//中序遍历中根节点左侧左子树交个子函数处理
root.left=builderTreeHelper(preorder,inorder,left,pos-1);
root.right=builderTreeHelper(preorder,inorder,pos+1,right);
return root;
}
/**
* 在中序遍历中找到根节点所对应的位置
* */
private int find(int val,int[] inOrder){
//遍历数组
for (int i = 0; i < inOrder.length;i++) {
if(inOrder[i]==val){
return i;
}
}
return -1;
}
}
4.5 leetcode106中序和后序遍历结果构建二叉树
/**
* 给定中序和后序遍历结果构建二叉树
* @author hide_on_bush
* @date 2022/6/22
*/
public class Num106_InOrderAndPostOrder {
//后序遍历倒置处理到第几个节点
private int index=0;
public TreeNode buildTree(int[] inorder, int[] postorder) {
//倒置后序遍历结果
reverse(postorder);
return buildTreeHelper(postorder,inorder,0,inorder.length-1);
}
private TreeNode buildTreeHelper(int[] postorder, int[] inorder, int left, int right) {
if(left>right){
return null;
}
if(index==postorder.length){
return null;
}
TreeNode root=new TreeNode(postorder[index]);
index++;
//从前序遍历找到的根节点找到对应中序遍历的索引
int pos=find(root.val,inorder);
root.right=buildTreeHelper(postorder,inorder,pos+1,right);
root.left=buildTreeHelper(postorder,inorder,left,pos-1);
return root;
}
private int find(int val, int[] inorder) {
for (int i = 0; i < inorder.length; i++) {
if(inorder[i]==val){
return i;
}
}
//不会返回-1,题中要求后序的结果在中序都能找到
return -1;
}
private void reverse(int[] postorder) {
int left=0;
int right=postorder.length-1;
while(left<right){
int tmp=postorder[left];
postorder[left]=postorder[right];
postorder[right]=tmp;
left++;
right--;
}
}
}
4.3和4.4两个问题总结(重点)
1.为什么4.3中可以通过前序遍历结果构建出二叉树,而4.4中必须要前序遍历结果和中序遍历结果才可以构建二叉树?
2.为什么4.3中的index++需要加两次,而4.4中只需要index++一次?
包含空节点,如果不index++会一直停留在空null

4.6nowCoder JZ36二分搜索树与双向链表
添加链接描述
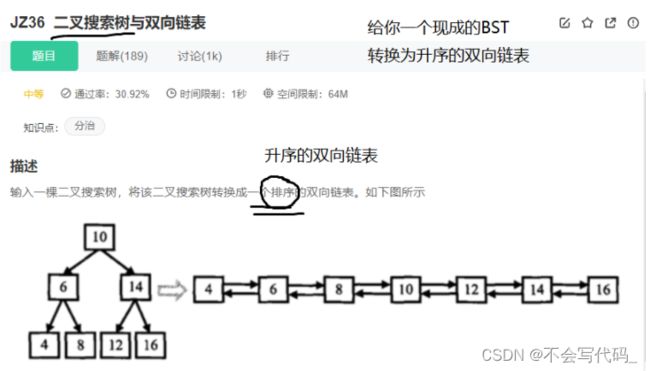
根据题目要求将树的节点想象成链表的节点

解题思路:把握递归语义
第一步:

第二步:

第三步:
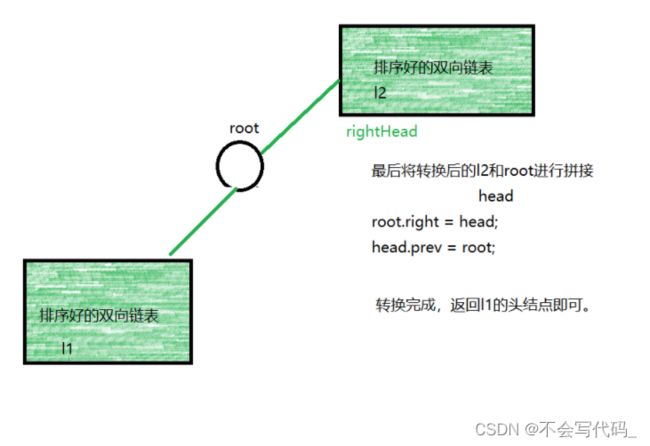
递归展开图在5_16的板书中
/**
* 传入一个BST根节点,就能转变为链表,并返回链表头节点
* @author hide_on_bush
* @date 2022/6/23
*/
public class NowCoder_Bst2List {
public TreeNode Convert(TreeNode pRootOfTree) {
//边界条件
if(pRootOfTree==null){
return null;
}
//1.将左子树转换为排序后的双向链表
TreeNode leftHead=Convert(pRootOfTree.left);
//2.找到左链表的尾结点和当前根节点拼接
TreeNode leftTail=leftHead;
//遍历链表
while(leftTail!=null&&leftTail.right!=null){
leftTail=leftTail.right;
}
//此时走到了左链表的尾结点,拼接链表
//可能存在左子树为空的情况
if(leftTail!=null){
leftTail.right=pRootOfTree;
pRootOfTree.left=leftTail;
}
//3.将右子树转化为双向链表
TreeNode rightHead=Convert(pRootOfTree.right);
//拼接右链表,只需要和头节点拼接即可
if(rightHead!=null){
pRootOfTree.right=rightHead;
rightHead.left=pRootOfTree;
}
//返回链表头节点,还需要再判断一次左子树是否为空
return leftHead==null?pRootOfTree:leftHead;
}
}
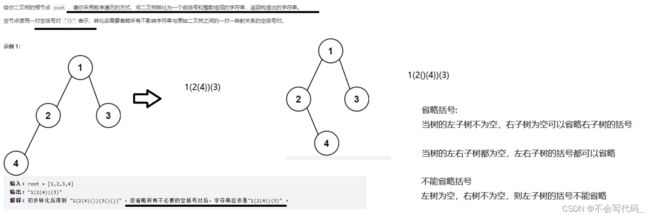
4.7二叉树创建字符串
/**
* 传入一棵二叉树根节点就能转换为字符串
* @author hide_on_bush
* @date 2022/6/23
*/
public class Num606_Tree2Str {
StringBuilder sb=new StringBuilder();
public String tree2str(TreeNode root) {
if(root==null){
return "";
}
//1.处理根节点
sb.append(root.val);
//2.处理左子树
if(root.left!=null){
sb.append("(");
tree2str(root.left);
sb.append(")");
}else{
//左子树为空右子树不为空补上()
if(root.right!=null){
sb.append("()");
}
}
//3.处理右子树
if(root.right!=null){
sb.append("(");
tree2str(root.right);
sb.append(")");
}
return sb.toString();
}
}