Java集合与数据结构——二叉树02
文章目录
- Java集合与数据结构——二叉树(二)初阶面试题
-
- 二叉树的前中后遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 获取二叉树的高度
- 获取二叉树的最大深度
- 求整颗二叉树的叶子节点数量
- 遍历思路:
- 子问题思路:
- 查找二叉树中 对应 val 值 的节点
- 判断两颗二叉树是否相同
- 另一棵树的子树
- 判断平衡二叉树
Java集合与数据结构——二叉树(二)初阶面试题
二叉树的前中后遍历
前序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> ret = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null){
return ret;
}
ret.add(root.val);
preorderTraversal(root.left);
preorderTraversal(root.right);
return ret;
}
}
中序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> ret = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null){
return ret;
}
preorderTraversal(root.left);
ret.add(root.val);
preorderTraversal(root.right);
return ret;
}
}
后序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> ret = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null){
return ret;
}
preorderTraversal(root.left);
preorderTraversal(root.right);
ret.add(root.val);
return ret;
}
}
获取二叉树的高度
获取二叉树的最大深度
public int gethigh(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = gethigh(root.left);
int rightHeight = gethigh(root.right);
return (Math.max(leftHeight, rightHeight))+1;
// 可用三目操作符来进行比较
// return (leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1 ) ;
}
求整颗二叉树的叶子节点数量
遍历思路:
遍历二叉树的每一个节点,如果该节点的左子树和右子树 都为空,那么该节点就为叶子节点,我们要计算叶子节点的数量,定义一个 leafSize ,当节点符合叶子节点的要求时 leafSize ++.
static int leafSize = 0;
public void getleafSize(TreeNode root) {
if(root == null){
return;
}
if((root.left == null && root.right == null ){
leafSize++;
}
getleafSize(root.left);
getleafSize(root.right);
}
子问题思路:
我们将求二叉树的叶子节点数量这个问题,看成求 二叉树的 左子树的叶子节点 + 右子树的叶子节点
当 root == null 时 返回0
当 root.right == null && root.left == null 时,返回1
public int getLeafSize2(TreeNode root) {
if(root == null){
return 0;
}
if(root.right == null && root.left == null){
return 1;
}
return getLeafSize2(root.left)+getLeafSize2(root.right);
}
子问题思路:
求第K层 有多少个节点
k=3 时, root 为第一层,我们求第三层相当于求 root.left 的第二层+ root.right 的第二层
同理可得我们最后求的是
root.left.left 的第一层 + root.left.right 的第一层 + root.right.left 的第一层 + root.right.right 的第一层
我们只需要判断此时 k==1 时的节点 是否为空就可以得到第K层的节点,这同时也体现了递归的思路。
我们可以将返回值这样写
return getLevelSize(root.left,k-1) + getLevelSize (root.right,k-1)
public int getLevelSize(TreeNode root,int k){
if(root == null){
return 0;
}
if(k==1){
return 1;
}
return getLevelSize(root.left,k-1)+getLevelSize(root.right,k-1);
}
查找二叉树中 对应 val 值 的节点
不考虑重复节点!!!
// 查找二叉树中 对应 val 值 的节点
TreeNode find(TreeNode root , char val){
if(root == null){
return null;
}
if(root.val == val){
return root;
}
TreeNode ret = find(root.left, val);
if(ret != null){
return ret;
}
ret = find(root.right,val);
if(ret != null){
return ret;
}
return null;
}
判断两颗二叉树是否相同
思路:
考虑 一个为空 一个不为空
两个都为空
两个都不为空时,值不一样
两个都不为空时,首个根的值是一样的
之后我们用递归来判断这两个根节点的左子树和右子树是否相同
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p != null && q == null){
return false;
}
if(p == null && q !=null){
return false;
}
if(p == null && q == null){
return true;
}
if(p.val != q.val){
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
}
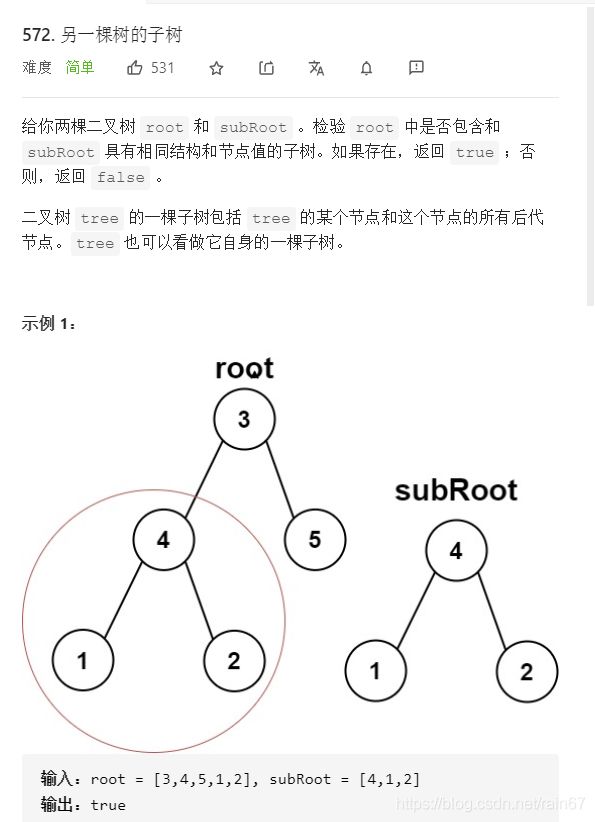
另一棵树的子树
我们来看一组树与子树
思路:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSameTree(TreeNode root, TreeNode subRoot){
if(root == null && subRoot != null){
return false;
}
if(subRoot == null && root != null){
return false;
}
if(subRoot == null && root == null){
return true;
}
if(root.val != subRoot.val){
return false;
}
return isSameTree(root.left,subRoot.left) && isSameTree(root.right,subRoot.right);
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root == null || subRoot == null){
return false;
}
if(isSameTree(root,subRoot)== true){
return true;
}
if(isSubtree(root.left,subRoot)) return true;
if(isSubtree(root.right,subRoot)) return true;
return false;
}
}
判断平衡二叉树
什么是平衡二叉树呢?
这颗二叉树的每一个节点的左右子树的高度差绝对值不超过1
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return (Math.max(leftHeight, rightHeight))+1;
}
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
int rightHeight = maxDepth(root.right);
int leftHeight = maxDepth(root.left);
return
Math.abs(rightHeight-leftHeight)<2 && isBalanced(root.left) && isBalanced(root.right);
}
}
上述的这种解法 时间复杂度太大了,遍历了每一个节点,在遍历节点的同时还要计算这个节点的深度,相当于右遍历了一遍,所以就是时间复杂度为 O(n^2)
时间复杂度太大了,我们换一种思路。
public int maxHeight(TreeNode root){
if(root==null){
return 0;
}
int leftHeight = maxHeight(root.left);
int rightHeight = maxHeight(root.right);
// 只要根的左树 或者右树 不满足,那么就会一直返回 -1,最后返回的就是一个负数,那么只要返回的不是正数就不是平衡二叉树
if(leftHeight>=0 && rightHeight>=0 && Math.abs(leftHeight-rightHeight)<2){
return Math.max(leftHeight,rightHeight)+1;
}else{
return -1;
}
}
public boolean isBalanced(TreeNode root) {
if(root==null){
return true;
}
return maxHeight(root)>=0;
这种解法时间复杂度为 O(n).
这一篇就结束了,今天二叉树就讲到这里,希望大家多多练习,谢谢大家的阅读与欣赏…
二叉树03------进阶编程练习 敬请期待~~