【opencv450-samples】图像配准 image_alignment.cpp

/*
* 本示例演示函数的使用
* findTransformECC 实现图像对齐ECC算法
*
*
* 演示加载图像（默认为 fruits.jpg），并根据给定的运动类型人工创建模板图像。
 当给定两幅图像时，第一幅图像是输入图像，第二幅图像定义模板图像。
 在后一种情况下，您还可以解析经纱的初始化。
输入和输出扭曲文件由原始扭曲（变换）元素组成
*
* 作者：G. Evangelidis，INRIA，格勒诺布尔，法国
* M. Asbach，Fraunhofer IAIS，德国圣奥古斯丁
*/

平移运动：

 欧式运动：euclidean

仿射运动：

透视扭曲运动：

源码：

 

/*
* This sample demonstrates the use of the function
* findTransformECC that implements the image alignment ECC algorithm
*
*
* The demo loads an image (defaults to fruits.jpg) and it artificially creates
* a template image based on the given motion type. When two images are given,
* the first image is the input image and the second one defines the template image.
* In the latter case, you can also parse the warp's initialization.
*
* Input and output warp files consist of the raw warp (transform) elements
*
* Authors: G. Evangelidis, INRIA, Grenoble, France
*          M. Asbach, Fraunhofer IAIS, St. Augustin, Germany
*/
#include 
#include 
#include 
#include 
#include 

#include 
#include 
#include 
#include 
#include 


using namespace cv;
using namespace std;

static void help(const char** argv);
static int readWarp(string iFilename, Mat& warp, int motionType);
static int saveWarp(string fileName, const Mat& warp, int motionType);
static void draw_warped_roi(Mat& image, const int width, const int height, Mat& W);

#define HOMO_VECTOR(H, x, y)\
    H.at(0,0) = (float)(x);\
    H.at(1,0) = (float)(y);\
    H.at(2,0) = 1.;

#define GET_HOMO_VALUES(X, x, y)\
    (x) = static_cast (X.at(0,0)/X.at(2,0));\
    (y) = static_cast (X.at(1,0)/X.at(2,0));


const std::string keys =
"{@inputImage    | fruits.jpg    | input image filename }"
"{@templateImage |               | template image filename (optional)}"
"{@inputWarp     |               | input warp (matrix) filename (optional)}"
"{n numOfIter    | 50            | ECC's iterations }"
"{e epsilon      | 0.0001        | ECC's convergence epsilon }"
"{o outputWarp   | outWarp.ecc   | output warp (matrix) filename }"
"{m motionType   | homography        | type of motion (translation, euclidean, affine, homography) }"
"{v verbose      | 1             | display initial and final images }"
"{w warpedImfile | warpedECC.png | warped input image }"
"{h help | | print help message }"
;


static void help(const char** argv)
{

    cout << "\nThis file demonstrates the use of the ECC image alignment algorithm. When one image"
        " is given, the template image is artificially formed by a random warp. When both images"
        " are given, the initialization of the warp by command line parsing is possible. "
        "If inputWarp is missing, the identity transformation initializes the algorithm. \n" << endl;

    cout << "\nUsage example (one image): \n"
        << argv[0]
        << " fruits.jpg -o=outWarp.ecc "
        "-m=euclidean -e=1e-6 -N=70 -v=1 \n" << endl;

    cout << "\nUsage example (two images with initialization): \n"
        << argv[0]
        << " yourInput.png yourTemplate.png "
        "yourInitialWarp.ecc -o=outWarp.ecc -m=homography -e=1e-6 -N=70 -v=1 -w=yourFinalImage.png \n" << endl;

}
//读取扭曲矩阵
static int readWarp(string iFilename, Mat& warp, int motionType) {

    // it reads from file a specific number of raw values:
    // 9 values for homography, 6 otherwise 它从文件中读取特定数量的原始值：单应性为 9 个值，否则为 6 个//
    CV_Assert(warp.type() == CV_32FC1);
    int numOfElements;
    if (motionType == MOTION_HOMOGRAPHY)//运动类型
        numOfElements = 9;
    else
        numOfElements = 6;

    int i;
    int ret_value;

    ifstream myfile(iFilename.c_str());
    if (myfile.is_open()) {
        float* matPtr = warp.ptr(0);//获取扭曲矩阵指针
        for (i = 0; i < numOfElements; i++) {
            myfile >> matPtr[i];
        }
        ret_value = 1;
    }
    else {
        cout << "Unable to open file " << iFilename.c_str() << endl;
        ret_value = 0;
    }
    return ret_value;
}
//保存扭曲矩阵
static int saveWarp(string fileName, const Mat& warp, int motionType)
{
    // it saves the raw matrix elements in a file
    CV_Assert(warp.type() == CV_32FC1);

    const float* matPtr = warp.ptr(0);//获取扭曲矩阵指针 
    int ret_value;//返回值： 1-保存成功

    ofstream outfile(fileName.c_str());//输出文件流
    if (!outfile) {
        cerr << "error in saving "
            << "Couldn't open file '" << fileName.c_str() << "'!" << endl;
        ret_value = 0;
    }
    else {//save the warp's elements  保存扭曲矩阵元素  https://www.jianshu.com/p/bb9c73b4a44b
        outfile << matPtr[0] << " " << matPtr[1] << " " << matPtr[2] << endl; //空格隔开一行三个
        outfile << matPtr[3] << " " << matPtr[4] << " " << matPtr[5] << endl;
        if (motionType == MOTION_HOMOGRAPHY) { //运动类型  平移（MOTION_TRANSLATION） 欧氏（MOTION_EUCLIDEAN） 仿射（MOTION_AFFINE） 单应性（MOTION_HOMOGRAPHY）
            outfile << matPtr[6] << " " << matPtr[7] << " " << matPtr[8] << endl;
        }
        ret_value = 1;
    }
    return ret_value;

}

//绘制扭曲的ROI 四边形边框
static void draw_warped_roi(Mat& image, const int width, const int height, Mat& W)
{
    Point2f top_left, top_right, bottom_left, bottom_right;
    //3x1矩阵
    Mat  H = Mat(3, 1, CV_32F);
    Mat  U = Mat(3, 1, CV_32F);
    //变换矩阵
    Mat warp_mat = Mat::eye(3, 3, CV_32F);
    //赋值
    for (int y = 0; y < W.rows; y++)
        for (int x = 0; x < W.cols; x++)
            warp_mat.at(y, x) = W.at(y, x);

    //warp the corners of rectangle 扭曲矩形的角点

    // top-left     H: [1,1,1]
    HOMO_VECTOR(H, 1, 1);
    /** @brief 执行广义矩阵乘法。
    函数 cv::gemm 执行类似于 BLAS 级别 3 中的 gemm 函数的广义矩阵乘法。例如，
    `gemm(src1, src2, alpha, src3, beta, dst, GEMM_1_T + GEMM_3_T)`
    对应于
    \f[\texttt{dst} = \texttt{alpha} \cdot \texttt{src1} ^T \cdot \texttt{src2} + \texttt{beta} \cdot \texttt{src3} ^T\f]

    如果是复数（双通道）数据，则执行复数矩阵乘法。

    该函数可以替换为矩阵表达式。例如，上面的调用可以替换为：
    @代码{.cpp}
        dst = alpha*src1.t()*src2 + beta*src3.t();
    @endcode
    @param src1 首先相乘的输入矩阵可以是实数（CV_32FC1，CV_64FC1）或复数（CV_32FC2，CV_64FC2）。
    @param src2 与 src1 相同类型的第二个相乘输入矩阵。
    @param 矩阵乘积的 alpha 权重。
    @param src3 添加到矩阵乘积的第三个可选增量矩阵；它应该与 src1 和 src2 具有相同的类型。
    @param src3 的 beta 权重。
    @param dst 输出矩阵；它具有适当的大小和与输入矩阵相同的类型。
    @param flags 操作标志 (cv::GemmFlags)
    @sa mulTransposed ，变换
    */
    gemm(warp_mat, H, 1, 0, 0, U);
    GET_HOMO_VALUES(U, top_left.x, top_left.y);

    // top-right
    HOMO_VECTOR(H, width, 1);
    gemm(warp_mat, H, 1, 0, 0, U);
    GET_HOMO_VALUES(U, top_right.x, top_right.y);

    // bottom-left
    HOMO_VECTOR(H, 1, height);
    gemm(warp_mat, H, 1, 0, 0, U);
    GET_HOMO_VALUES(U, bottom_left.x, bottom_left.y);

    // bottom-right
    HOMO_VECTOR(H, width, height);
    gemm(warp_mat, H, 1, 0, 0, U);
    GET_HOMO_VALUES(U, bottom_right.x, bottom_right.y);//单应性变换后的右下角点

    // draw the warped perimeter 绘制弯曲的周长
    line(image, top_left, top_right, Scalar(255));
    line(image, top_right, bottom_right, Scalar(255));
    line(image, bottom_right, bottom_left, Scalar(255));
    line(image, bottom_left, top_left, Scalar(255));
}

//https://www.jianshu.com/p/bb9c73b4a44b 
int main(const int argc, const char* argv[])
{

    CommandLineParser parser(argc, argv, keys);
    parser.about("ECC demo");

    parser.printMessage();
    help(argv);

    string imgFile = parser.get(0);//场景图像路径
    string tempImgFile = parser.get(1);//模板图像路径
    string inWarpFile = parser.get(2);//输入的扭曲矩阵文件

    int number_of_iterations = parser.get("n");//迭代次数
    double termination_eps = parser.get("e");//终止精度
    string warpType = parser.get("m");//运动变换类型
    int verbose = parser.get("v");//是否输出cout内容 
    string finalWarp = parser.get("o");//最终的扭曲矩阵
    string warpedImFile = parser.get("w");//扭曲的图像文件
    if (!parser.check())
    {
        parser.printErrors();
        return -1;
    }
    //运动变换类型
    if (!(warpType == "translation" || warpType == "euclidean"
        || warpType == "affine" || warpType == "homography"))
    {
        cerr << "Invalid motion transformation" << endl;
        return -1;
    }

    int mode_temp;
    if (warpType == "translation")
        mode_temp = MOTION_TRANSLATION;//平移（MOTION_TRANSLATION）：图像可以被移位（x，y）来获得第二个图像，我们只需要估算两个参数x和y。
    else if (warpType == "euclidean")
        mode_temp = MOTION_EUCLIDEAN;//欧氏（MOTION_EUCLIDEAN）：图像的旋转和移位版本。所以有三个参数x，y和角度。
    else if (warpType == "affine")
        mode_temp = MOTION_AFFINE;//仿射（MOTION_AFFINE）：仿射变换是旋转、平移（移位）、缩放和剪切的组合，该变换有六个参数。当正方形经历仿射变换时，平行线保持平行，但是以直角相交的线不再保持正交。
    else
        mode_temp = MOTION_HOMOGRAPHY;//单应性（MOTION_HOMOGRAPHY）：上述所有变换都是2D变换。它们不考虑3D效果。另一方面，单应性变换可以解释一些3D效果（但不是全部）。该变换有8个参数。使用单应性转换时的正方形可以更改为任何四边形。


    Mat inputImage = imread(samples::findFile(imgFile), IMREAD_GRAYSCALE);//读取灰度空间图像
    if (inputImage.empty())
    {
        cerr << "Unable to load the inputImage" << endl;
        return -1;
    }

    Mat target_image;
    Mat template_image;

    if (tempImgFile != "") {
        inputImage.copyTo(target_image);
        template_image = imread(samples::findFile(tempImgFile), IMREAD_GRAYSCALE);//模板图像
        if (template_image.empty()) {
            cerr << "Unable to load the template image" << endl;
            return -1;
        }

    }
    else { //apply random warp to input image 对输入图像应用随机扭曲//
        resize(inputImage, target_image, Size(216, 216), 0, 0, INTER_LINEAR_EXACT);//缩放原图
        Mat warpGround;
        RNG rng(getTickCount());
        double angle;
        switch (mode_temp) {//对原图缩放后进行随机变换 得到模板
        case MOTION_TRANSLATION://平移运动
            warpGround = (Mat_(2, 3) << 1, 0, (rng.uniform(10.f, 20.f)),
                0, 1, (rng.uniform(10.f, 20.f)));//随机平移矩阵
            warpAffine(target_image, template_image, warpGround,
                Size(200, 200), INTER_LINEAR + WARP_INVERSE_MAP);//进行平移。  
            break;
        case MOTION_EUCLIDEAN://欧式运动
            angle = CV_PI / 30 + CV_PI * rng.uniform((double)-2.f, (double)2.f) / 180;

            warpGround = (Mat_(2, 3) << cos(angle), -sin(angle), (rng.uniform(10.f, 20.f)),
                sin(angle), cos(angle), (rng.uniform(10.f, 20.f)));//随机欧式变换矩阵
            warpAffine(target_image, template_image, warpGround,
                Size(200, 200), INTER_LINEAR + WARP_INVERSE_MAP);//平移+旋转
            break;
        case MOTION_AFFINE://仿射变换

            warpGround = (Mat_(2, 3) << (1 - rng.uniform(-0.05f, 0.05f)),
                (rng.uniform(-0.03f, 0.03f)), (rng.uniform(10.f, 20.f)),
                (rng.uniform(-0.03f, 0.03f)), (1 - rng.uniform(-0.05f, 0.05f)),
                (rng.uniform(10.f, 20.f)));//随机仿射变换矩阵
            warpAffine(target_image, template_image, warpGround,
                Size(200, 200), INTER_LINEAR + WARP_INVERSE_MAP);
            break;
        case MOTION_HOMOGRAPHY://单应性变换  透视变换 https://zhuanlan.zhihu.com/p/60482480
            warpGround = (Mat_(3, 3) << (1 - rng.uniform(-0.05f, 0.05f)),
                (rng.uniform(-0.03f, 0.03f)), (rng.uniform(10.f, 20.f)),
                (rng.uniform(-0.03f, 0.03f)), (1 - rng.uniform(-0.05f, 0.05f)), (rng.uniform(10.f, 20.f)),
                (rng.uniform(0.0001f, 0.0003f)), (rng.uniform(0.0001f, 0.0003f)), 1.f);//随机3x3单应性变换矩阵
            warpPerspective(target_image, template_image, warpGround,
                Size(200, 200), INTER_LINEAR + WARP_INVERSE_MAP);//透视变换： 随机扭曲原图得到模板图像
            break;
        }
    }
    /** @brief 对图像应用仿射变换。
    CV_EXPORTS_W void warpAffine( InputArray src, OutputArray dst,
                              InputArray M, Size dsize,
                              int flags = INTER_LINEAR,
                              int borderMode = BORDER_CONSTANT,
                              const Scalar& borderValue = Scalar());
        函数 warpAffine 使用指定的矩阵变换源图像：

        \f[\texttt{dst} (x,y) = \texttt{src} ( \texttt{M} _{11} x + \texttt{M} _{12} y + \texttt{M} _{13 }, \texttt{M} _{21} x + \texttt{M} _{22} y + \texttt{M} _{23})\f]

        当设置标志 #WARP_INVERSE_MAP 时。否则，先用#invertAffineTransform 反转变换，然后代入上面的公式，而不是M。该函数不能就地操作。

        @param src 输入图像。
        @param dst 输出图像，其大小为 dsize 且类型与 src 相同。
        @param M \f$2\times 3\f$ 变换矩阵。
        @param dsize 输出图像的大小。
        @param 标志插值方法的组合（请参阅#InterpolationFlags）和可选标志 #WARP_INVERSE_MAP，这意味着 M 是逆变换（ \f$\texttt{dst}\rightarrow\texttt{src}\f$ ）。
        @param borderMode 像素外推方法（参见#BorderTypes）；当borderMode=#BORDER_TRANSPARENT时，表示目标图像中与源图像中的“异常值”对应的像素未被函数修改。
        @param borderValue 值在恒定边框的情况下使用；默认情况下，它是 0。

        @sa warpPerspective，调整大小，重新映射，getRectSubPix，变换
         */


         /** @example samples/cpp/warpPerspective_demo.cpp
         示例程序显示使用 cv::getPerspectiveTransform 和 cv::warpPerspective 进行图像变形
         */

         /** @brief 对图像应用透视变换。
         CV_EXPORTS_W void warpPerspective( InputArray src, OutputArray dst,
                                       InputArray M, Size dsize,
                                       int flags = INTER_LINEAR,
                                       int borderMode = BORDER_CONSTANT,
                                       const Scalar& borderValue = Scalar());
         函数 warpPerspective 使用指定的矩阵变换源图像：

         \f[\texttt{dst} (x,y) = \texttt{src} \left ( \frac{M_{11} x + M_{12} y + M_{13}}{M_{31} x + M_ {32} y + M_{33}} ,
              \frac{M_{21} x + M_{22} y + M_{23}}{M_{31} x + M_{32} y + M_{33}} \right )\f]

         当设置标志 #WARP_INVERSE_MAP 时。否则，先用 invert 反转变换，然后代入上面的公式，而不是 M。该函数不能就地操作。

         @param src 输入图像。
         @param dst 输出图像，其大小为 dsize 且类型与 src 相同。
         @param M \f$3\times 3\f$ 变换矩阵。
         @param dsize 输出图像的大小。
         @param 标志插值方法（#INTER_LINEAR 或 #INTER_NEAREST）和可选标志 #WARP_INVERSE_MAP 的组合，它将 M 设置为逆变换（
         \f$\texttt{dst}\rightarrow\texttt{src}\f$）。
         @param borderMode 像素外推方法（#BORDER_CONSTANT 或 #BORDER_REPLICATE）。
         @param borderValue 值在恒定边框的情况下使用；默认情况下，它等于 0。

         @sa warpAffine，调整大小，重新映射，getRectSubPix，perspectiveTransform
          */
    const int warp_mode = mode_temp; //变换模式

    // 初始化或加载扭曲矩阵initialize or load the warp matrix
    Mat warp_matrix;
    if (warpType == "homography")
        warp_matrix = Mat::eye(3, 3, CV_32F);//透视变换矩阵
    else
        warp_matrix = Mat::eye(2, 3, CV_32F);//仿射变换矩阵

    if (inWarpFile != "") {
        int readflag = readWarp(inWarpFile, warp_matrix, warp_mode);//扭曲矩阵文件
        if ((!readflag) || warp_matrix.empty())
        {
            cerr << "-> Check warp initialization file" << endl << flush;
            return -1;
        }
    }
    else {

        printf("\n ->Performance Warning: Identity warp ideally assumes images of "
            "similar size. If the deformation is strong, the identity warp may not "
            "be a good initialization. \n");

    }

    if (number_of_iterations > 200)
        cout << "-> Warning: too many iterations " << endl;

    if (warp_mode != MOTION_HOMOGRAPHY) //仿射变换矩阵2x3
        warp_matrix.rows = 2;

    // start timing
    const double tic_init = (double)getTickCount();//开始计时
    double cc = findTransformECC(template_image, target_image, warp_matrix, warp_mode,
        TermCriteria(TermCriteria::COUNT + TermCriteria::EPS,
            number_of_iterations, termination_eps));//计算模板图像与原图像的 扭曲变换矩阵

    if (cc == -1)
    {//执行中断    检查扭曲矩阵初始化  以及 图像尺寸
        cerr << "The execution was interrupted. The correlation value is going to be minimized." << endl;
        cerr << "Check the warp initialization and/or the size of images." << endl << flush;
    }

    // end timing
    const double toc_final = (double)getTickCount();//结束计时
    const double total_time = (toc_final - tic_init) / (getTickFrequency());//总时间
    if (verbose) {
        cout << "Alignment time (" << warpType << " transformation): "
            << total_time << " sec" << endl << flush;//
        //  cout << "Final correlation: " << cc << endl << flush;

    }

    // 保存最终的扭曲矩阵save the final warp matrix
    saveWarp(finalWarp, warp_matrix, warp_mode);

    if (verbose) {
        cout << "\nThe final warp has been saved in the file: " << finalWarp << endl << flush;
    }

    //保存最终扭曲的图像 save the final warped image
    Mat warped_image = Mat(template_image.rows, template_image.cols, CV_32FC1);
    if (warp_mode != MOTION_HOMOGRAPHY)//仿射变换
        warpAffine(target_image, warped_image, warp_matrix, warped_image.size(),
            INTER_LINEAR + WARP_INVERSE_MAP);
    else//透视变换
        warpPerspective(target_image, warped_image, warp_matrix, warped_image.size(),
            INTER_LINEAR + WARP_INVERSE_MAP);//利用计算的扭曲矩阵 扭曲源图像 得到warped_image扭曲后的图像

    //save the warped image
    imwrite(warpedImFile, warped_image);

    // display resulting images
    if (verbose)
    {

        cout << "The warped image has been saved in the file: " << warpedImFile << endl << flush;

        namedWindow("image", WINDOW_AUTOSIZE);
        namedWindow("template", WINDOW_AUTOSIZE);
        namedWindow("warped image", WINDOW_AUTOSIZE);
        namedWindow("error (black: no error)", WINDOW_AUTOSIZE);

        moveWindow("image", 20, 300);
        moveWindow("template", 300, 300);
        moveWindow("warped image", 600, 300);
        moveWindow("error (black: no error)", 900, 300);

        // draw boundaries of corresponding regions
        Mat identity_matrix = Mat::eye(3, 3, CV_32F);//单位矩阵

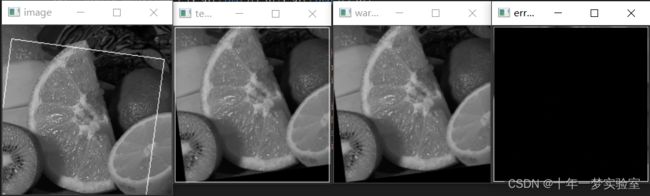
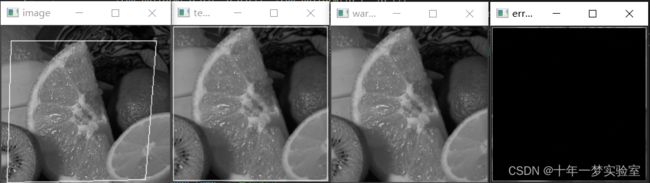
        draw_warped_roi(target_image, template_image.cols - 2, template_image.rows - 2, warp_matrix);//绘制扭曲的周边（四条边）
        draw_warped_roi(template_image, template_image.cols - 2, template_image.rows - 2, identity_matrix);//绘制模板图像的周边

        Mat errorImage;
        subtract(template_image, warped_image, errorImage);//模板图像与扭曲后的图像相减
        double max_of_error;
        minMaxLoc(errorImage, NULL, &max_of_error);//最大误差像素点

        // show images
        cout << "Press any key to exit the demo (you might need to click on the images before)." << endl << flush;

        imshow("image", target_image);//显示目标图像
        waitKey(200);
        imshow("template", template_image);//显示模板图像
        waitKey(200);
        imshow("warped image", warped_image);//显示扭曲的图像
        waitKey(200);
        imshow("error (black: no error)", abs(errorImage) * 255 / max_of_error);//误差图像灰度化
        waitKey(0);

    }

    // done
    return 0;
}