Deep Residual Learning for Image Recognition论文翻译(非google翻译)
Deep Residual Learning for Image Recognition
- 基于深度残差学习的图像识别
-
- 摘要
- 1 引言(Introduction)
- 2 相关工作(RelatedWork)
- 3 Deep Residual Learning
-
- 3.1 残差学习(Residual Learning)
- 3.2 通过快捷方式进行恒等映射(Identity Mapping by Shortcuts)
- 3.3 网络体系结构(Network Architectures)
- 3.4 实现(Implementation)
- 4 实验(Experiments)
-
- 4.1 ImageNet分类(ImageNet Classification)
- 4.2 CIFAR-10与分析(CIFAR-10 and Analysis)
- 4.3 基于PASCAL和MS-COCO的目标检测(Object Detection on PASCAL and MS COCO)
论文翻译pdf及翻译markdown文件:论文原版及翻译及笔记
resnet代码实现及代码流程图和讲解:resnet代码实现及代码流程图和讲解
基于深度残差学习的图像识别
摘要
更深层次的神经网络更难训练。(批注:提出问题)我们提出了一个残差学习框架,以简化对比以前使用的网络进行更深的网络训练。我们根据层输入显式地将层重新表示为学习残差函数( learning residual functions),而不是学习未定义函数。我们提供了综合的经验证据,表明这些残差网络更易于优化,并且可以从大幅度增加的深度中获得精度。(批注:随着深度的增加,精度也会提升)在ImageNet数据集上,我们估计残差网络的深度可达152层–是vgg网络的8倍深[41],但仍然具有较低的复杂性。这些残差网的集合在图像集上的误差达到了3.57%。 这个结果获得了ILSVRC2015的分类任务第一名,我们还用CIFAR-10数据集分析了100层和1000层的网络。
表示的深度对于许多视觉识别任务是非常重要的。仅仅由于我们的表示非常深入,我们在coco对象检测数据集上得到了28%的相对改进。 深度残差网络是我们参加ILSVRC & COCO 2015 竞赛上所使用模型的基础,并且我们在ImageNet检测、ImageNet定位、COCO检测以及COCO分割上均获得了第一名的成绩。
1 引言(Introduction)
(批注:摘要的一个详细解释)
深层卷积神经网络[22,21]导致了图像分类[21,50,40]的一系列突破。深层网络自然地将低/中/高层次特征[50]和分类器以端到端的多层方式集成在一起,而特征的“层次”可以通过堆叠层的数量((深度)来丰富。最近的证据[41,44]表明,网络深度至关重要,在富有挑战性的ImageNet数据集[36]上的领先结果[41,44,13,16]都利用了“非常深”[41]模型,深度为16[41]至30[16]。许多其他非平凡(nontrivial)的视觉识别任务[8,12,7,32,27]也从非常深的模型中获益良多。
在深度重要性的驱动下,出现了一个问题:学习更好的网络就像堆积更多的层一样容易吗?回答这个问题的一个障碍是众所周知的梯度消失/爆炸[1,9]的问题,它从一开始就阻碍了收敛(hamper convergence )。然而,这个问题在很大程度上是通过标准化初始化[23,9,37,13]和中间归一化层(batch normalization)[16]来解决的,这使得数十层的网络在反向传播的随机梯度下降(SGD)上能够收敛。
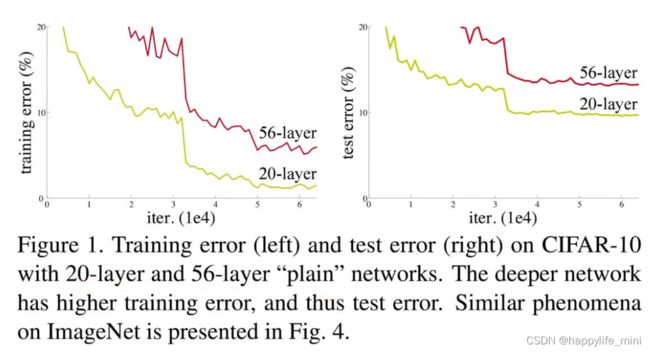
当更深的网络能够开始收敛时,就会暴露出一个退化问题:随着网络深度的增加,准确性达到饱和(这可能不足为奇),然后迅速退化。出乎意料的是,这种退化不是由过度拟合引起的,在[10,41]中有阐释,并由我们的实验充分验证了,将更多层添加到适当深度的模型中会导致更高的训练误差。(**批注:**ovefitting是训练比较好而测试不好,但现在情况是更深的网络训练的也不是很好)图1显示了一个典型示例。
图1、20层和56层“朴素”网络的CIFAR-10上的训练错误(左)和测试错误(右)。网络越深,训练误差越大,测试误差越大。图4中给出了ImageNet上的类似现象。
(训练精度的)退化表明,并非所有网络结构都同样容易优化。让我们考虑一个较浅的网络和一个与其对应的更深的结构(批注:更深的网络指的是在浅层网络再加一些层上去),它会在其上添加更多层。对于构建更深层的模型,我们可以找到一种解决方案:添加的层是恒等映射,而其他层是从学习的浅层模型中复制的。该构造解决方案的存在表明,较深的模型不会产生比浅模型更高的训练误差。(批注:如果浅层网络训练的不错,深层网络效果不应该变差,所以在之后加入恒等映射的层,理论不变差,但是实际结果变差了)但是实验表明,我们现有的求解器无法找到解决方案比构造的解决方案好或更好(或在可行时间内无法做到)。
在本文中,我们通过引入深度残差学习框架(deep residual learning framework)来解决退化问题。我们不是希望每个堆叠的层都直接适合所需的基础映射,而是显式地让这些层拟合一个残差映射(residual mapping)。 假设所需的底层映射为 H(x),我们让堆叠的非线性层来拟合另一个映射: F(x):=H(x)−x。 因此原来的映射转化为: F(x)+x。我们假设优化残差映射比优化原始的未参考的映射容易。在极端情况下,如果恒等映射是最优的,则将残差推至零比用一堆非线性层拟合恒等映射更容易。(批注:核心思想,假如已经有一个模型学得了x,在之后加入新的层,假如原来新加入的层要学习的是H(x),现在不学H(x),而换成学习H(x)-x,那么其实新加入的层学习的是真实值与之前学得的值的残差)
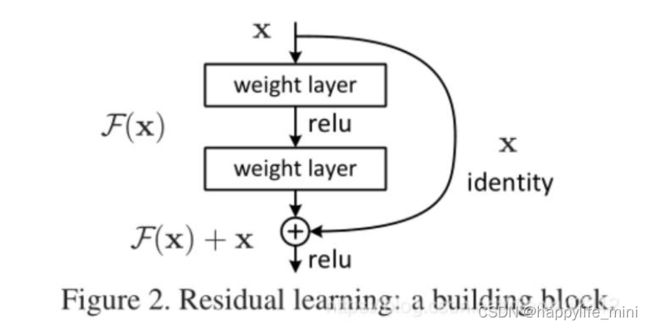
公式 F(x)+x 可以通过前馈神经网络( feedforward neural networks )的**“快捷连接(shortcut connections)”**来实现(图2)。(批注:在上个世纪90年代已经被提出)shortcut connections[2,34,49]是跳过一个或多个层的连接。在本例中,shortcut connections只执行恒等映射,它们的输出被添加到叠加层的输出中(图2)。**恒等捷径连接既不增加额外的参数,也不增加计算的复杂性。**整个网络仍然可以使用反向传播的SGD进行端到端的训练,并且可以使用公共库(例如caffe[19])来实现,而无需修改求解器( solvers)。
图2、残差学习:一个积木块
我们在ImageNet[36]上进行了综合实验,以说明退化问题并对我们的方法进行评估。结果表明:
1) 我们的极深残差网络易于优化,但对应的“朴素”网(即简单的层叠层)随着深度的增加,训练误差较大;
2) 我们的深层残差网可以很容易地从深度的大幅度增加中获得精度增益,比以前的网络产生的结果要好得多。
CIFAR-10数据集上也出现了类似的现象,这表明了我们提出的方法的优化难度和效果并不仅仅是对于一个特定数据集而言的。我们在这个数据集上展示了经过成功训练的100层以上的模型,并探索了1000层以上的模型。
在ImageNet分类集[36]上,我们利用极深的残差网得到了很好的结果。我们的152层剩余网是迄今为止在ImageNet上出现的最深的网络,但其复杂度仍然低于vgg网络[41]。我们的组合在ImageNet测试集上有3.57%的前5错误( top-5 error),并在ILSVRC 2015分类竞赛中获得了第一名。他在其他识别任务上也有很好的泛化能力,使我们在ILSVRC中的图像网络检测、图像网络定位、coco检测和coco分割方面获得了第一名。这一强有力的证据表明,残差学习原理是通用的,我们期望它适用于其他视觉和非视觉问题。
2 相关工作(RelatedWork)
(批注:概述之前别人已经做的一些相关工作)
**残差表示。**在图像识别中,VLAD[18]是用残差向量对字典进行编码的表示,Fisher向量[30]可以表示为VLAD的概率版本[18]。两者都是图像检索和分类的有力表示法[4,48]。对于矢量量化,编码剩余向量[17]比编码原始矢量更有效。
在低水平视觉和计算机图形学中,对于求解偏微分方程(PDEs),广泛使用的多重网格方法[3]在多尺度上将系统重新定义为子问题,其中每个子问题负责较粗和较细尺度之间的残差解( residual solution )。多重网格的另一种选择是分层基预处理( hierarchical basis preconditioning)[45,46],它依赖于在两个尺度之间表示残差向量的变量。[3,45,46]已证明这些求解器比不知道解的残差性质的标准求解器收敛得快得多。这些方法表明,一个好的配方或预处理可以简化优化。
快捷连接。 捷径连接[2, 34, 49] 已经经过了很长的一段实践和理论研究过程。一个训练多层感知器(MLPs)的早期实践是添加一个线性层,从网络输入连接到输出[34,49]。在[44,24]中,一些中间层直接连接到辅助分类器,用于解决消失/爆炸梯度(的问题)。[39,38,31,47]的论文提出了用捷径连接实现集中层响应、梯度和传播误差的方法。在[44]中,“Inception”层是由一个捷径分支和几个更深的分支组成的。
与此同时,“ 高速网“(”highway networks”)[42,43]将捷径连接与门控函数[15]结合起来。这些门依赖于数据,并且有参数,而我们的恒等快捷连接( identity shortcuts )是无参数的。当门控捷径“关闭”(接近于零)时,公路网中的层表示非残差函数。相反,我们的公式总是学习残差函数;我们的恒等快捷连接永远不会关闭,所有信息都会被传递出去,而附加的残差函数将被学习。此外,高速网络在深度极深(例如,超过100层)的情况下,没有表现出精确性的提高。
3 Deep Residual Learning
3.1 残差学习(Residual Learning)
让我们把H(x)看作是由几个层叠层(不一定是整个网)组成的底层映射,用x表示这些层中的第一个层的输入。如果假设多个非线性层可以渐近逼近复杂函数[28],则等于假设它们可以渐近逼近残差函数,即H(X)−x(假设输入和输出具有相同的维度)。因此,与其期望叠加层近似H(X),我们不如显式地让这些层近似一个残差函数F(x):=H(x)−x。原来的函数因此变成F(x)+x。虽然这两种形式都应该能够渐近地近似于所期望的函数(如假设),但学习的容易程度可能是不同的。
该种**重新表示( reformulation)**是由有关退化问题的反直觉现象所驱动的(图1,左)。正如我们在介绍中所讨论的,如果可以将添加的层构造为恒等映射,则更深层次的模型应该具有不大于其浅层结构的训练错误。退化问题表明求解者很难用多个非线性层逼近恒等映射。利用残差学习重构,如果恒等映射是最优的,则求解者可以简单地将多个非线性层的权值推向零,以逼近恒等映射。
在实际情况下,恒等映射不太可能是最优的,但是我们的重新表达对于这个问题的预处理是有帮助的。如果最优函数更接近于恒等映射而不是零映射,则求解者应该更容易找到与恒等映射有关的扰动(perturbations),而不是将其作为新的扰动来学习。我们通过实验(图7)证明了学习的残差函数一般都有较小的响应,说明恒等映射提供了合理的预条件。
3.2 通过快捷方式进行恒等映射(Identity Mapping by Shortcuts)
我们对每几个层叠的层次采用残差学习。图2中展示出了一个积木块(building block )。形式上,在本文中,我们考虑了一个积木块被定义为:
y = F(x, {Wi}) + x. (1)
这里x和y是考虑的层的输入和输出向量。函数![]() 表示要学习的残差映射。 图2中的例子包含两层,
表示要学习的残差映射。 图2中的例子包含两层,![]() ,其中σ代表ReLU,为了简化省略了偏置项。F+x操作由一个快捷连接和元素级(element-wise)的加法来表示。在加法之后我们再执行另一个非线性操作(例如, σ(y),如图2)。
,其中σ代表ReLU,为了简化省略了偏置项。F+x操作由一个快捷连接和元素级(element-wise)的加法来表示。在加法之后我们再执行另一个非线性操作(例如, σ(y),如图2)。
公式(1)中的shortcut连接没有增加额外的参数和计算复杂度。这不仅在实践中很有吸引力,而且在我们比较普通网络和残差网络时也很重要。 我们可以在参数、深度、宽度以及计算成本都相同的基础上对两个网络进行公平的比较(除了可以忽略不计的元素级的加法)。
在等式(1)中,x和F的维数必须相等。如果情况并非如此(例如,在更改输入/输出通道时),我们可以通过快捷连接执行线性投影Ws ,以匹配维度:
y = F(x, {Wi}) +Wsx. (2)
在等式(2)中,我们还可以使用方阵Ws。但是,我们将通过实验证明,恒等映射对于解决退化问题是足够的,而且是经济的,因此只有在匹配维数时才使用Ws。
残差函数F的形式是灵活的。本文的实验涉及一个函数F,它有两个或三个层(图5),然而它可能有更多的层。但如果F只有一个单层,则公式1类似于线性层:y=w1x+x,对此我们没有发现任何优势。
我们还注意到,虽然为了简单起见,上述表示法是关于全连通层的,但它们适用于卷积层。函数F(x,{wi})可以表示多个卷积层。元素级加法是在两个特征映射上相应通道上执行的。.
3.3 网络体系结构(Network Architectures)
我们测试了各种普通/残差网络,并观察到一致的现象。为了提供讨论的实例,我们对ImageNet的两个模型进行了如下描述。
Plain网络。 我们的plain网络结构(图3,中)主要受VGG网络 (图.3,左)的启发。卷积层主要为3*3的滤波器,并遵循以下两点要求:(i) 输出特征映射尺寸相同的层含有相同数量的滤波器;(ii) 如果特征尺寸减半,则滤波器的数量增加一倍来保证每层的时间复杂度相同。我们直接用步长为2的卷积层进行下采样。网络以一个全局平均池层和一个带有Softmax的1000路全连接层结束。在图3(中),有权值的层的总数为34 。
图3 对应于ImageNet的网络框架举例。 左:VGG-19模型 (196亿个FLOPs)作为参考。中:plain网络,含有34个参数层(36 亿个FLOPs)。右:残差网络,含有34个参数层(36亿个FLOPs)。虚线表示的shortcuts增加了维度。Table 1展示了更多细节和其它变体。
值得注意的是,与vgg网[41](图3,左)相比,我们的模型具有更少的滤波器和更低的复杂度。我们的34层基线(baseline)有36亿FLOPs乘加),仅为VGG-19(196亿FLOPs)的18%。
**残差网络。**基于上述plain网络,我们插入快捷连接(图3,右)将网络转换为对应的残差版本。当输入和输出尺寸相同时(图3中的实线快捷连接),可以直接使用恒等快捷键(公式1)。 当维度增加时(表3中的虚线部分),考虑两个选项:
(A) shortcut仍然使用恒等映射,在增加的维度上使用0来填充,这样做不会增加额外的参数;
(B) 使用公式2的映射shortcut来使维度保持一致(通过11的卷积)。 对于这两个选项,当shortcut跨越两种尺寸的特征图时,均使用stride为2的卷积。**(批注:1 * 1的特征图可以任意改变深度,例如,32 32* 64的特征图,经过256个1* 1* 64的卷积核,最终得到32* 32*256的特征图)**
3.4 实现(Implementation)
我们对ImageNet的实现遵循了[21,41]中的做法。 调整图像的大小使它的短边长度随机的从[256,480] 中采样来进行尺寸扩展( scale augmentation)[41]。 从图像或其水平翻转中随机抽取224×224 crop,并减去每个像素平均(the per-pixel mean)[21]。使用了[21]中的标准颜色增强。我们遵循[16],在每次卷积之后,在激活之前采用批归一化(BN)[16]。我们像[13]一样初始化权重,从零开始训练所有plain/残差网。我们使用小批量大小为256的SGD。学习速率从0.1开始,当误差稳定时除以10,并且 整个模型进行60∗10^4次迭代训练。(批注:迭代次数通常会根据batch size的大小进行改变,所以现在一般说为训练多少遍数据集)我们使用的权重衰减为0.0001,动量为0.9。(批注:现在比较标准的参数初始化)我们不使用Dropout[14],按照[16]的做法。
在测试中,为了进行比较,我们采取标准的10-crop测试。 为了取得最好的效果,我们采用了[41,13]中的全卷积形式,并且在多尺度上平均分数(图像被调整大小,使较短的一面为{224,256,386,480,640}(批注:不同的分辨率))。
4 实验(Experiments)
4.1 ImageNet分类(ImageNet Classification)
我们在ImageNet 2012分类数据集[36]上评估了我们的方法,该数据集包含1000个类。模型在128万张训练图像上进行了训练,在50k张验证图像上进行了评估。我们还获得了测试服务器报告的100k张测试图像的最终结果。我们评估了前1位和前5位的错误率(top-1 and top-5 error rates)。
**普通的网络。**我们首先评估18层和34层普通网络。34层普通网在图3(中)。18层普通网具有类似的形式.详细的体系结构见表1。
表1. 对应于ImageNet的结构框架。括号中为构建块的参数(同样见Fig.5),数个构建块进行堆叠。下采样由stride为2的conv3_1、conv4_1和conv5_1 来实现。
(批注:对于更深的网络结构如50,101,152层的resnet,使用的更深的瓶颈设计bottleneck,用1* 1的卷积修改通道数)
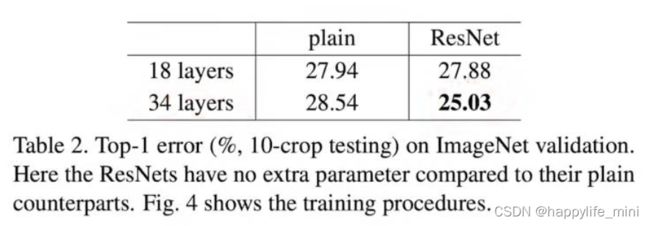
表2的结果表明,较深的34层普通网比较浅的18层普通网具有更高的验证误差。为了揭示原因。在图4(左)中,我们在训练过程中比较他们的训练/验证错误。我们在整个训练过程中观察到了34层普通网的退化问题—它在整个训练过程中训练误差较大,尽管18层普通网的解空间( solution space)是34层普通网的子空间。
表2、ImageNet验证上的Top-1错误(%,10-crop 测试)。在这里,与普通的对等网相比,残差网没有额外的参数。图4展示了培训过程。
我们认为这种优化困难不太可能是由梯度消失引起的。这些简单的网络使用BN[16]进行训练,从而确保前向传播的信号具有非零方差。我们还验证了使用BN的向后传播梯度具有健康的行为(norms)。所以无论向前还是向后信号都不会消失。事实上,34层普通网仍然能够达到具有竞争力的精度(表3),这表明求解器在某种程度上可以工作。我们推测深普通网可能具有指数级别的低收敛速度,从而影响训练误差的减小【3–我们已经试验了更多的训练迭代(3×),并仍然观察到退化问题,这表明这个问题不可能通过简单地使用更多的迭代来解决】。这种优化困难的原因将在今后进行研究。
**残差网络。**接下来,我们评估18层和34层残差网(ResNet).基线结构与上述普通网相同,只是要求在每对3×3过滤器中添加一个快捷连接,如图3(右)所示。在第一个比较中(表2和图4右),我们使用所有快捷方式为恒等映射,以及使用零填充增加维度(选项A)。因此,与普通的对应网络相比,它们没有额外的参数。
图4、关于ImageNet的训练。细曲线表示训练误差,粗体曲线表示中心crop的验证误差。左:18层和34层的普通网络。右:18层和34层残差网络。在此图中,与普通网络相比,残差网络没有(增加)额外的参数。
我们从表2和图4中有三个主要的观察结果。首先,使用残差学习的情况与之前(普通网)相反----34层ResNet优于18层 ResNet(2.8%).更重要的是,34层ResNet的训练误差要小得多,并且可以推广到验证数据。这表明,在这种情况下,退化问题得到了很好的解决,并且我们设法从增加的深度中获得了精度增益。(批注:红色的较细的线表示的是训练误差,之所以训练误差会大于测试误差,是因为在训练中使用大量数据增强,使得训练误差较大,而测试的时候未做数据增强,噪音比较低;在线的下坡位置是学习率的下降,学习率乘以0.1,在获得一定收敛后减小学习率,对数据进行更精确的训练,但现在应用较少,因为在何时修改是不确定的。现在用cos(x)的曲线作为学习率的下降速度,取得了比较好的结果。)
第二,与普通的对应网络相比,34层ResNet使Top-1误差减少了3.5%(表2),这是成功地减少了训练误差(图2)的结果(图4右 VS 左))。这一比较验证了残差学习在极深系统上的有效性。
最后,我们还注意到,18层普通/残差网具有大致相等的精确率(表2),但18层ResNet的收敛速度更快(图4右 VS 左)。当网络“不太深”(比如这里的18层)时,当前的SGD解决程序仍然能够为普通网络找到好的解决方案。在这种情况下,ResNet通过在早期阶段提供更快的收敛速度来简化优化。
恒等快捷键 VS **投影快捷键( Projection Shortcuts)。**我们已经证明,无参数的恒等快捷键有助于训练。接下来我们研究投影快捷键(公式2。在表3中,我们比较了三个选项:
(A)零填充快捷键用于增加维度,所有快捷方式都是无参数的(与表2和图4右相同);
(B)投影快捷键用于增加尺寸,而其他快捷键是恒等快捷键;
©所有快捷键都是投影快捷键。
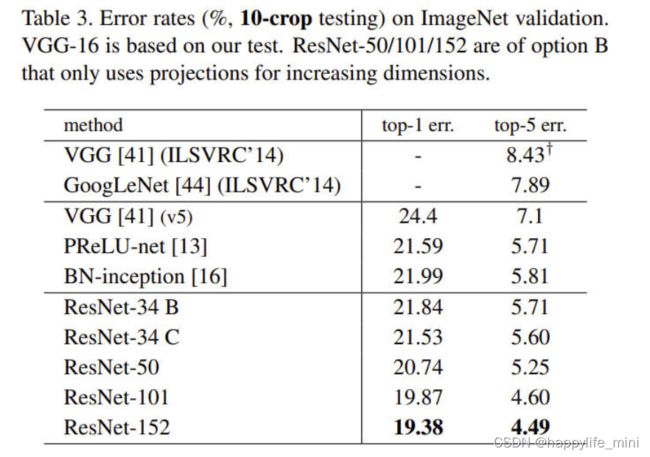
表3、对ImageNet验证的错误率(%,10-crop测试)。vgg-16是基于我们的测试。ResNet-50/101/152属于方案B ,它只对增加的维度使用投影(快捷键)。
表3显示,所有这三个选项都比普通的对应方案要好得多。B比A稍好,我们认为,这是因为A中零填充的维度实际上并没有(使用)残差学习。C比B略好,我们把这归因于许多(13个)投影快捷键引入的额外参数。但是a/b/c之间的小差异表明,投影快捷键对于解决退化问题并不重要。因此,在本文的其余部分中,我们不使用选项c以降低计算/时间复杂度和模型大小。恒等快捷键对于不增加下面介绍的瓶颈架构(bottleneck architectures)的复杂性特别重要。(批注:投影短连接会增大计算复杂度,现在resnet都是使用B方案,即用1* 1卷积做一次投影)
更深层次的瓶颈架构。(批注:构建更深的resnet)接下来,我们将描述我们针对ImageNet的更深层次的网络。由于考虑到我们负担得起的训练时间,我们将积木块(building block)修改为瓶颈设计(bottleneck design)。对于每个残差函数F,我们使用一个由3层组成的堆栈,而不是2层(图5)。这三层分别是1×1、3×3和1×1卷积,其中1×1层负责减小然后增加(恢复)维数,使3×3层成为输入/输出维数较小的瓶颈(批注:减少计算)。图5给出了一个例子,其中两种设计都具有相似的时间复杂度。
图5、ImageNet的一个更深层次的残差函数F。左图:如图3所示的用于ResNet-34的一个及积木块(在56×56特征图上)。右:ResNet-50/101/152的“瓶颈”积木块。
无参数的恒等快捷键对于瓶颈架构尤其重要。如果是图5(右)中的同恒等快捷键用投影快捷键代替,可以看出时间复杂度和模型大小加倍,因为快捷方式连接到两个高维端点。因此,恒等快捷键为瓶颈设计提供了更有效的模型。
50层ResNet:我们将34层网络中的每个2层块替换为这个3层瓶颈块,从而形成一个50层ResNet(表1)。我们使用选项B来增加维度。这种模式有38亿次FLOPs。
**101层和152层 ResNet:**我们使用更多的三层块来构造101层和152层的ResNet(表1)。值得注意的是,虽然深度明显增加,但152层 ResNet((113亿次 FLOPs)的复杂性仍然低于vgg-16/19网(153/196亿次 FLOPs)。
50/101/152层ResNet比34层网有相当大程度的准确率提升(表3和表4)。我们没有观察到退化的问题,因此,我们可以享受从大大增加的深度中获得的显著的精确性。所有评价指标都能看到深度的好处(表3和表4)。
表4、ImageNet验证集上单模型结果的错误率(%)(除了†报告了测试集)。
**和最先进的方法比较。**在表4中,我们将与之前最好的单模型结果进行比较。我们的基线34层ResNet已经达到了非常竞争的准确性。我们的152层 ResNet的单模型Top-5验证误差为4.49%。这个单一模型的结果优于所有以前的集成结果(表5)。我们将六个不同深度的模型组合成一个整体(在提交时只有两个152层网络)。这将得到了测试集上3.57%的Top-5错误(表5).这一项目获得了2015年ILSVRC的第一名。
4.2 CIFAR-10与分析(CIFAR-10 and Analysis)
我们在CIFAR-10数据集[20]进行了更多的研究,该数据集包括50个训练图像和10个类别的10k测试图像。我们在训练集上进行了实验训练,并在测试集上进行了评估。我们的重点是极深网络的行为,而不是推进最先进的结果,所以我们故意使用简单的架构如下。
普通/残差结构遵循图3(中/右)中的形式。网络输入32×32图像,每像素被减去每像素平均( with the per-pixel mean subtracted)。第一层为3×3卷积层。然后,我们在尺寸为{32,16,8}的特征映射上分别使用3×3卷积的共6n层叠加,每个特征地图大小都有2n层。滤波数分别为{16,32,64}。下采样是以2的步长的卷积来执行的。网络以全局平均池、10路全连接层和softmax为结束。共有6n+2层加权层。下表概述了该体系结构:
当使用快捷连接时,它们被连接到3×3层的对上(总共3n条捷径)。在这个数据集中,我们在所有情况下都使用恒等快捷键(即选项A),因此,我们的残差模型的深度、宽度和参数与对应的普通模型完全相同。
我们使用权重衰减为0.0001,动量为0.9,采用了在[13]中的权值初始化在[13]和bn[16],但没有使用Dropout。这些模型是在两个GPU上训练的,小批量大小为128。我们的学习速度为0.1,在第32K和48K次迭代时除以10,在64k迭代时终止训练,这是由45k/5k训练/验证的分割决定。我们按照[24]中的简单数据增强进行训练:每边填充4个像素,从填充图像或水平翻转中随机抽取32×32帧。对于测试,我们只评估原始32×32图像的单一图像。
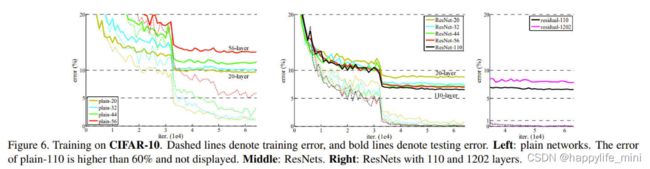
我们比较n={3,5,7,9},从而形成的20,32,44和56层网络。图6(左)显示了普通网的行为。深普通网随着深度增大,深度训练误差较大。这个现象类似于ImageNet(图4左)和mnist(见[42])上的现象,这表明这种优化困难是一个基本问题。
图6、在CIFAR-10上的训练。虚线表示训练错误,粗体线表示测试错误。左:普通网络。普通-110的误差大于60%,不显示。中间:残差网。右:有110层和1202层的残差网。
我们进一步探索了当n=18时获得的110层ResNet。在这种情况下,我们发现初始学习速率0.1太大,以致无法开始收敛。因此,我们使用0.01的学习速率为训练热身,直到训练误差小于80%(约400次迭代),然后将学习速率改为0.1继续训练。学习计划的其余部分和以前一样。这个110层网络能够很好地收敛(图6, 中)。它的参数比 FitNet[35]和 Highway42等其他深而瘦的网络少,但却是最先进的结果之一(6.43%,表6)。
表6、CIFAR-10测试集的分类错误。所有方式都有数据增强。对于ResNet-110,我们运行5次,显示“最佳(平均±STD)”,如[43]中。
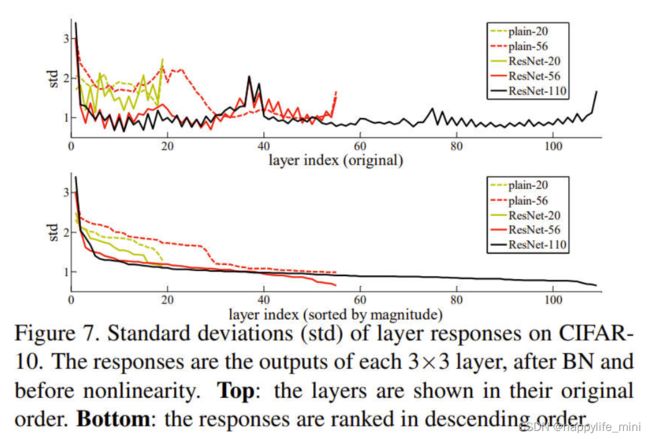
**层响应分析。**图7显示层响应的标准差(std)。响应为每个3×3层的输出,它在BN之后,在其它非线性(relu/加法)之前。对于ResNet,本分析揭示了残差函数的响应强度。图7表明残差网的响应一般比普通网的小。这些结果支持了我们的基本动机(第3.1节),即残差函数一般比非残差函数更接近于零。我们还注意到,较深的ResNet的响应幅度较小,如图7中ResNet-20、56和110之间的比较所示。当有更多的层时,单个的一层残差网倾向于对信号进行较少的修改。(**批注:假如后面更深的层没有使得模型变得更好,由于有残差连接的存在,所以新加的层不会学到任何东西,权值都是靠近0;**意思就是说就算有1000层的东西,但是也就前100层有用,而后面900层基本上没有什么东西可以学习,这个现象在图上有所显示,但是由于普通网络和resnet用的相同的参数,普通网络根本没有训练好,所以无法对比)
图7、CIFAR-10层响应的标准差(STD)。响应是每个3×3层的输出,在BN之后,在非线性之前。顶部:各层按原来的顺序显示。底部:响应按降序排列。
**探索超过1000层(的网络)。**我们探索了一个超过1000层的深度模型。我们设置n=200得到1202层网络,该网络就像上面所描述的那样被训练。我们的方法不存在优化困难,该1000层网络的训练误差小于0.1%(图6,右)。它的测试误差仍然相当好(7.93%,表6)。
但在这些激进的深层次模型上,仍存在一些有待解决的问题。这个1202层网络的测试结果比我们的110层网络差,尽管两者都有相似的训练误差。我们认为这是因为过拟合。对于这个小数据集,1202层网络可能不必要地大(19.4M)。在此数据集使用强正则化,如maxout[10]或dropout[14],可以获得最佳结果([10,25,24,35]。但在本文中,我们使用的是无 maxout/无漏的方法,只需通过深而瘦的结构设计来实现正则化,而不分散对优化的困难的关注。但是,与更强的正则化相结合可以提高结果,这是我们今后研究的方向。
4.3 基于PASCAL和MS-COCO的目标检测(Object Detection on PASCAL and MS COCO)
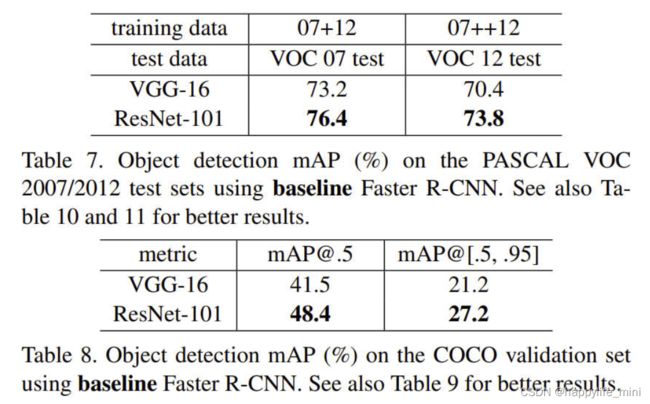
该方法对其它识别任务具有较好的泛化性能。表7和表8显示了PASCAL VOC 2007 and 2012[5]和COCO[26]的目标检测基线结果。我们采用Faster R-CNN[32]作为检测方法。在这里,我们对用ResNet-101替换VGG-16[41]的改进感兴趣。使用这两种模型的检测实现(见附录)是相同的,因此收益只能归功于更好的网络。最值得注意的是,在具有挑战性的coco数据集上,我们得到了coco标准度量的6.0%的增长(map@[.5,.95]),,这是一个28%的相对改进。这一收益完全归功于所学习的表述(learned representations)。
表7、在Pascal voc 2007/2012测试集上使用基线Faster R-CNN的目标检测 mAP(%)。更好的结果见10和11。
表8、在coco验证集上 使用基线Faster R-CNN的目标检测mAP(%)。另见表9,以获得更好的结果。
(批注:mAP是在目标检测上最常用的用于衡量锚框精度的指标,越高越好)
基于深度剩余网,我们在ILSVRC的几个项目中获得了第一名:Imagenet检测,ImageNet定位,coco检测和coco分割。详情见附录。
References(参考文献)
[1] Y. Bengio, P. Simard, and P. Frasconi. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on NeuralNetworks, 5(2):157–166, 1994.
[2] C. M. Bishop. Neural networks for pattern recognition. Oxford university press, 1995.
[3] W. L. Briggs, S. F. McCormick, et al. A Multigrid Tutorial. Siam, 2000.
[4] K. Chatfield, V. Lempitsky, A. Vedaldi, and A. Zisserman. The devil is in the details: an evaluation of recent feature encoding methods. In BMVC, 2011.
[5] M. Everingham, L. Van Gool, C. K. Williams, J. Winn, and A. Zis-serman. The Pascal Visual Object Classes (VOC) Challenge. IJCV, pages 303–338, 2010.
[6] S. Gidaris and N. Komodakis. Object detection via a multi-region & semantic segmentation-aware cnn model. In ICCV, 2015.
[7] R. Girshick. Fast R-CNN. In ICCV, 2015.
[8] R. Girshick, J. Donahue, T. Darrell, and J. Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In CVPR, 2014.
[9] X. Glorot and Y. Bengio. Understanding the difficulty of training deep feedforward neural networks. In AISTATS, 2010.
[10] I. J. Goodfellow, D. Warde-Farley, M. Mirza, A. Courville, and Y. Bengio. Maxout networks. arXiv:1302.4389, 2013.
[11] K. He and J. Sun. Convolutional neural networks at constrained time cost. In CVPR, 2015.
[12] K. He, X. Zhang, S. Ren, and J. Sun. Spatial pyramid pooling in deep convolutional networks for visual recognition. In ECCV, 2014.
[13] K. He, X. Zhang, S. Ren, and J. Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In ICCV, 2015.
[14] G. E. Hinton, N. Srivastava, A. Krizhevsky, I. Sutskever, and R. R. Salakhutdinov. Improving neural networks by preventing coadaptation of feature detectors. arXiv:1207.0580, 2012.
[15] S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.
[16] S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
[17] H. Jegou, M. Douze, and C. Schmid. Product quantization for nearest neighbor search. TPAMI, 33, 2011.
[18] H. Jegou, F. Perronnin, M. Douze, J. Sanchez, P. Perez, and C. Schmid. Aggregating local image descriptors into compact codes. TPAMI, 2012.
[19] Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S. Guadarrama, and T. Darrell. Caffe: Convolutional architecture for fast feature embedding. arXiv:1408.5093, 2014.
[20] A. Krizhevsky. Learning multiple layers of features from tiny images. Tech Report, 2009.
[21] A. Krizhevsky, I. Sutskever, and G. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012.
[22] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel. Backpropagation applied to hand-written zip code recognition. Neural computation, 1989.
[23] Y.LeCun, L.Bottou, G.B.Orr, andK.-R.Müller. Efficientbackprop. In Neural Networks: Tricks of the Trade, pages 9–50. Springer, 1998.
[24] C.-Y. Lee, S. Xie, P. Gallagher, Z. Zhang, and Z. Tu. Deeply-supervised nets. arXiv:1409.5185, 2014.
[25] M. Lin, Q. Chen, and S. Yan. Network in network. arXiv:1312.4400, 2013.
[26] T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollár, and C. L. Zitnick. Microsoft COCO: Common objects in context. In ECCV. 2014.
[27] J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In CVPR, 2015.
[28] G. Montúfar, R. Pascanu, K. Cho, and Y. Bengio. On the number of linear regions of deep neural networks. In NIPS, 2014.
[29] V. Nair and G. E. Hinton. Rectified linear units improve restricted boltzmann machines. In ICML, 2010.
[30] F. Perronnin and C. Dance. Fisher kernels on visual vocabularies for image categorization. In CVPR, 2007.
[31] T. Raiko, H. Valpola, and Y. LeCun. Deep learning made easier by linear transformations in perceptrons. In AISTATS, 2012.
[32] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: Towards real-time object detection with region proposal networks. In NIPS, 2015.
[33] S. Ren, K. He, R. Girshick, X. Zhang, and J. Sun. Object detection networks on convolutional feature maps. arXiv:1504.06066, 2015.
[34] B. D. Ripley. Pattern recognition and neural networks. Cambridge university press, 1996.
[35] A. Romero, N. Ballas, S. E. Kahou, A. Chassang, C. Gatta, and Y. Bengio. Fitnets: Hints for thin deep nets. In ICLR, 2015.
[36] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, et al. Imagenet large scale visual recognition challenge. arXiv:1409.0575, 2014.
[37] A. M. Saxe, J. L. McClelland, and S. Ganguli. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv:1312.6120, 2013.
[38] N. N. Schraudolph. Accelerated gradient descent by factor-centering decomposition. Technical report, 1998.
[39] N. N. Schraudolph. Centering neural network gradient factors. In Neural Networks: Tricks of the Trade, pages 207–226. Springer,1998.
[40] P. Sermanet, D. Eigen, X. Zhang, M. Mathieu, R. Fergus, and Y. Le- Cun. Overfeat: Integrated recognition, localization and detection using convolutional networks. In ICLR, 2014.
[41] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015.
[42] R. K. Srivastava, K. Greff, and J. Schmidhuber. Highway networks. arXiv:1505.00387, 2015.
[43] R. K. Srivastava, K. Greff, and J. Schmidhuber. Training very deep networks. 1507.06228, 2015.
[44] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. Going deeper with convolutions. In CVPR, 2015.
[45] R. Szeliski. Fast surface interpolation using hierarchical basis functions. TPAMI, 1990.
[46] R. Szeliski. Locally adapted hierarchical basis preconditioning. In SIGGRAPH, 2006.
[47] T. Vatanen, T. Raiko, H. Valpola, and Y. LeCun. Pushing stochastic gradient towards second-order methods–backpropagation learning with transformations in nonlinearities. In Neural Information Processing, 2013.
[48] A. Vedaldi and B. Fulkerson. VLFeat: An open and portable library of computer vision algorithms, 2008.
[49] W. Venables and B. Ripley. Modern applied statistics with s-plus. 1999.
[50] M. D. Zeiler and R. Fergus. Visualizing and understanding convolutional neural networks. In ECCV, 2014.