SVM的简单理解

1、基本知识
决策边界，或称为决策面，其目的是将两种类别的进行分开。

决策边界如何定义？训练集上的正负样本到决策边界的距离保持最大。

支撑向量是什么？可以理解为当前样本下，支撑当前决策边界的样本，如何支撑向量不变，继续增加训练样本，决策边界不会发生变化。

松弛因子ei（大于0），对约束进行放松，允许噪声点的存在，这个很重要，因为大部分情况下样本都是近似可分（即使在使用核函数的情况下），松弛因子的存在使寻找的决策边界更优。

惩罚项C（大于0），控制松弛因子ei的作用情况，当C很大，ei发挥的作用小，也就是松弛的少，当C很小，ei发挥的在作用大，松弛的多

SVM的目标函数与约束怎么来？
假设决策边界函数$g(x)=wx+b$,则样本点到$g(x)的距离为$
$$\frac{|g(x)|}{||w||}$$在SVM中只关注支撑样本点，然后取距离它们最远的平面为决策边界，转为数学公式为：$$max(min(\frac{|g(x)|}{||w||}))$$,可以简化成：$$max(\frac{1}{||w||})$$ $$s.t.y_i\ast g(x_i)\ge 1$$怎么来的呢？一般有$y_i=-1或1，|g(x)|\ge 1$所以推导得到

2、基本原理
假设给定样本集$D=(x_1,y_1),((x_2,y_2),\cdot \cdot \cdot ，((x_n,y_n)$,$y_i\in \{-1,1\}$样本容量为n，SVM的目的是寻找一个最佳分类面将两个类分开，这个分类分类面可以通过下述方程描述：
$$w^{T}x+b=0$$
$w$表示平面的方向；$b$表示偏离量，决定平面与原点的距离。

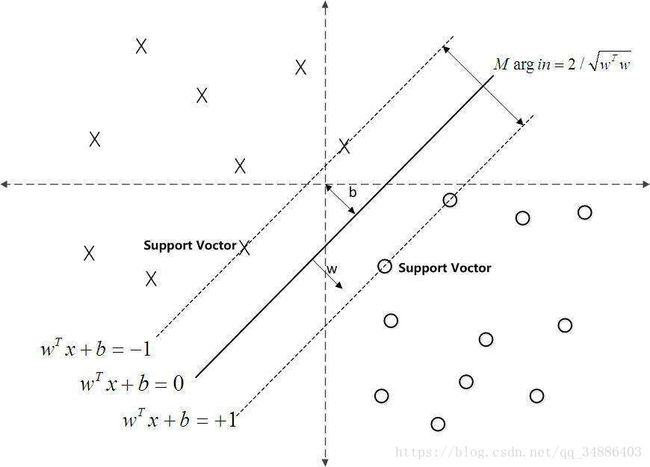
从上图可以看出左侧x点距离平面的距离是小于-1，二右侧的圆点到平面的距离是大于1的。由于$y_i$为-1或1，即可以用公式$y_i(wx+b)\ge +1$,当是支撑向量时，等号成立，即$wx+b=1$和$wx+b=-1$，将这两个平面的距离记为$\gamma$,SVM的核心就是尽量是间隔距离$\gamma$最大化。
记$wx+b=1$上的为正样本$x_{+}$，在$wx+b=-1$上的是负样本$x_{-}$，根据向量的加减法规则，$x_{+}$减去$x_{-}$得到的向量在最佳超平面的法向量$w$方向的投影即使距离$\gamma$:
$$\gamma =(x_{+}-x_{-})\frac{w}{||w||}=\frac{w{x}_{+}}{||w||}-\frac{w{x}_{-}}{||w||}$$
又有$w{x}_{+}=1-b$,$w{x}_{-}=-1-b$
所以得
$$\gamma =\frac{2}{||w||}$$
就是说距离$\gamma$决策面的法向量有关，要找到最大间隔的决策边界，只需找到满足约束条件下参数$w,b$使得$\gamma$最大，即有：

$$\{\begin{array}{r}ma{x}_{w,b}\frac{2}{||w||}\\ s.t{y}_i(wx+b)\ge +1\end{array}$$
一般转化为求最小值：
$$\{\begin{array}{r}mi{n}_{w,b}\frac{1}{2}||w|{|}^2\\ s.t{y}_i(wx+b)\ge +1\end{array}$$
这就是基本的SVM

---

结合之前提及到惩罚项C和松弛因子ei，优化的目标变为下述：

$$\{\begin{array}{r}mi{n}_{w,b}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^n{e}_i\\ s.t{y}_i(wx+b)\ge 1-e_i,i=1,2\cdot \cdot \cdot ,n\\ e_i\ge 0\end{array}$$
这是我们一般情况下使用的SVM