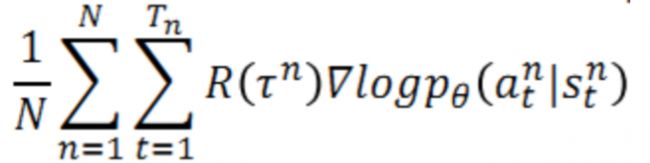李宏毅深度强化学习笔记

增强学习（RL）的一些基本概念：

RL的基本组成：

1-actor：即操纵/需要学习的对象，如飞机大战里的飞机

2-environment：外部环境，如飞机大战里除了飞机以外的所有东西，他们均为游戏内部设定

3-reward：回报，如飞机大战中打死一个飞机得到的分数

其中1是我们自己控制的，可以学习。2，3均无法控制。

三者相互作用的过程：

其中s为环境的状态state，a为actor的行动action。

某一次游戏/实验中的状态和行动组成的集合叫做轨迹$\tau :=\{(s_1,a_1),...,(s_t,a_t),...\}$

Policy：

一般用$\pi$表示，指的是给定环境的某状态s之后actor采取的行动a(的概率分布)。由于一般a都不是一个确定的值而是一个随机变量，所以Policy实际是一个概率分布。

在将RL和神经网络（NN）结合之后，Policy一般可以理解为一个参数为$\theta$的NN。其输入为状态s，输出为给定s之后对应的行动的概率分布的某个抽样。

轨迹的概率：

直观上，某个轨迹$\tau :=\{(s_1,a_1),...,(s_t,a_t),...\}$出现的概率，自然是给定的初始状态为$s_1$的概率$p(s_1)$，乘上给定$s_1$之后actor输出的action为$a_1$的概率$p_{\theta }(a_1|s_1)$的概率，乘以给定当前环境的状态$s_1$以及actor采取行动$a_1$之后环境的状态变为$s_2$的概率。乘以…即

$p_{\theta }(a_1|s_1)$：有了$s_1$之后采取的$a_1$不是固定的，而是随机的，符合一个概率分布。即NN的输出是一个概率分布，而真正采取到的action $a_1$是从这个分布中抽样得到的。

$p(s_2|s_1,a_1)$: 有了第一个画面$s_1$以及player的行为$a_1$之后游戏本身转化为的另一个画面$s_2$。这个东西由游戏本身决定，一般来说不是确定的，否则这个游戏就太过无聊了。

我们能控制的是前者，后者是游戏设定好的。

Expected Reward：

我们的目标就是最大化某次完整的实验(Episode)所得到的轨迹$\tau$对应的reward的总和。但由于状态s和行动a都是随机的，所以需要针对这些随机性取期望，即我们最大化的实际上是下面的Expected Reward：

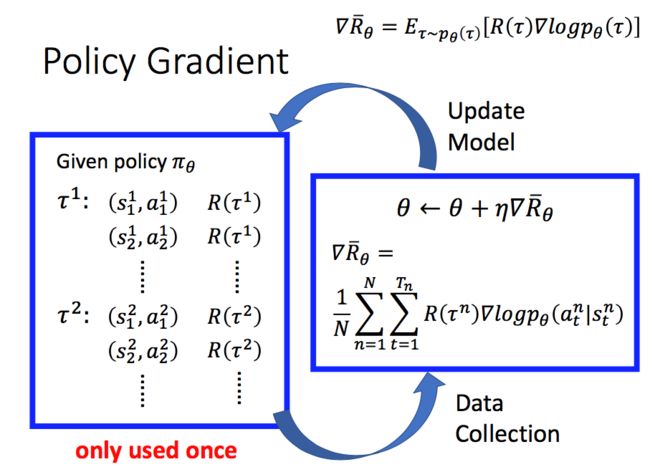
Policy gradient:

使用类似于GD的方法来优化上述目标函数：

其中倒数第二行的约等号是用样本平均代替期望值；

最后一行根据的是$p_{\theta }({\tau }^n)$的计算公式以及该公式中的一部分和$\theta$无关，所以求梯度后是0.

最后一行的直观：如果给定某个s时采取行为a得到的reward是正的，那么就要增加给定s时采取行为a的概率$p_{\theta }(a|s)$。

在实际应用中，为了更合理，需要对$R({\tau }^n)$进行一定的调整，一般通过添加基准线和考虑各个时间点的收益权重(添加权重因子)来将$R({\tau }^n)$转化为$A^{\theta }(s_t,a_t)$

---

On-policy$\to$Off-policy

回忆Policy gradient中梯度的最终结果

因此在用policy gradient迭代更新时，每迭代一次得到一个新的$\theta$之后，就需要用新的policy $\theta$与环境做互动很多次得到样本数据，才能再次更新$\theta$:

非常非常耗时。

接下来要提到的On-policy$\to$Off-policy就是为了解决这个计算量太大的问题。

首先介绍两者的概念：

On-policy：和环境交互的agent与学习的agent是同一个（比如阿光自己在和别人下棋，一边下棋一边学习）

Off-policy：上述的两个agent不是同一个（比如阿光在看两外两个人下棋，在一边学习）

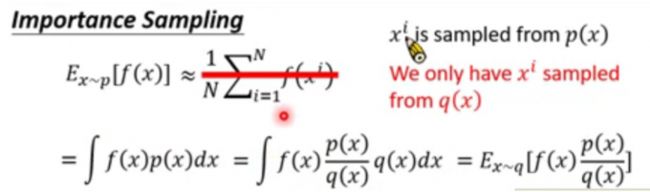
Importance Sampling：

为了实现On-policy$\to$Off-policy首先需要介绍一个更一般的数学概念Importance Sampling。他把关于一个概率分布求期望转化为了关于另一个概率分布取期望：

虽然理论上来说上述相等是严格的，但实际上我们计算期望的方式其实是样本平均，所以要想让两个样本平均近似相等，需要的一个要求就是$p,q$两个分布的差距不太大。

利用上述思想，就可以完成on policy到off policy的转化：

利用${\pi }_{\theta }^{\prime }$来进行采样，将采集的样本拿来训练$\theta$ ，由于$\theta \prime$是固定的，采集的样本可以被重复使用，即用一个${\theta }^{\prime }$采集到的样本进行多次$\theta$的更新。

PPO:

上面提到，为了保证On-policy$\to$Off-policy的准确性，需要$\theta ,{\theta }^{\prime }$两个分布非常相似。所以在真正用policy gradient优化时，目标函数需要在原来的基础上加一个惩罚项，即$\beta KL(\theta ,{\theta }^{\prime })$用来控制两个分布的差距。其中$\beta$是惩罚系数，可以手动调整。KL的意思是KL divergence

因此对于PPO，真正来优化的目标函数不是Expected Reward${\bar{R}}_{\theta }$，而是下面的：

注：

1-从${\bar{R}}_{\theta }$到$J^{{\theta }^{\prime }}(\theta )$的转化也需要一些技术细节，这里省略了中间过程。

2-这里的KL($\theta ,{\theta }^{\prime }$)并不是指做为分布时两个参数的KL divergence（做为分布时两者的KL divergence实验中是无法得到的），而是指两者behaviour上的距离，即根据两者的历史行为算出经验上的KL divergence。

实际算法如下：