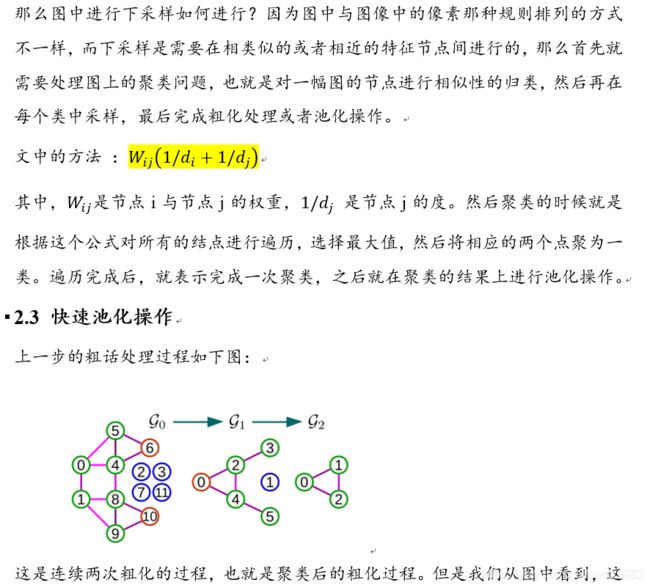
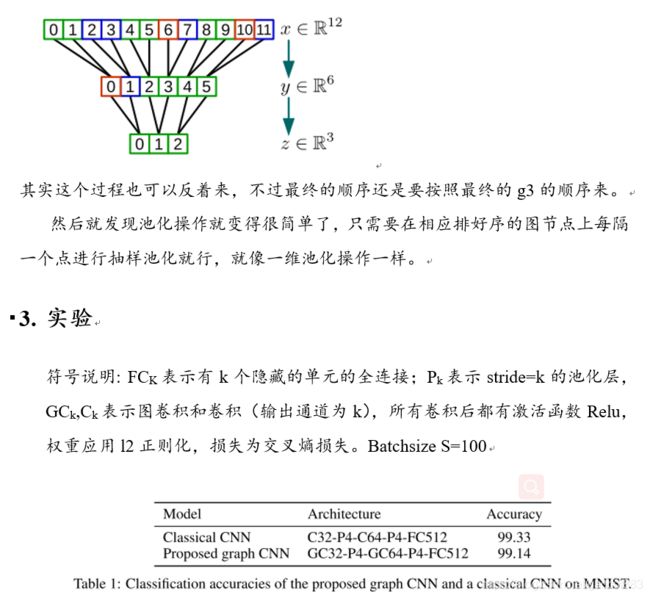
论文阅读笔记（6）: GNN-快速局部光谱滤波

• 实验：
  代码论文中有，这里只是解读部分代码：

# -*- coding: utf-8 -*- 
# author: cuihu
# time : 2021/4/10 15:07
# task:  本文图神经网络网的使用，详细请看论文
# 《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》

import sys
sys.path.append("./lib")
from lib import models, graph, coarsening, utils
import numpy as np
import matplotlib.pyplot as plt
import sklearn.metrics
import sklearn.neighbors
import matplotlib.pyplot as plt
import scipy.sparse
import scipy.sparse.linalg
import scipy.spatial.distance
import numpy as np

# step 1 step 1 step 1 step 1 step 1 step 1 step 1 step 1 step 1 step 1
# :建立数据。

d = 100    # Dimensionality.
n = 10000  # Number of samples.
c = 5      # Number of feature communities.

# Data matrix, structured in communities (feature-wise).
# 一共3类。
X = np.random.normal(0, 1, (n, d)).astype(np.float32)
X += np.linspace(0, 1, c).repeat(d // c)

# Noisy non-linear target.
w = np.random.normal(0, .02, d)
t = X.dot(w) + np.random.normal(0, .001, n)
t = np.tanh(t)
# plt.figure(figsize=(15, 5))
# plt.plot(t, '.')
# # plt.show()
# Classification.
y = np.ones(t.shape, dtype=np.uint8)
y[t > t.mean() + 0.4 * t.std()] = 0
y[t < t.mean() - 0.4 * t.std()] = 2
print('Class imbalance: ', np.unique(y, return_counts=True)[1])
# [3592 3057 3351]
# 划分数据集：
n_train = n // 2
n_val = n // 10

X_train = X[:n_train]
X_val   = X[n_train:n_train+n_val]
X_test  = X[n_train+n_val:]

y_train = y[:n_train]
y_val   = y[n_train:n_train+n_val]
y_test  = y[n_train+n_val:]

##### step2 ##### step2 ##### step2 ##### step2 ##### step2 ##### step2
# 根据数据集的特性建立图，也就是相应的邻接矩阵，这里使用的方法像素之间的欧式距离。
def distance_scipy_spatial(z, k=4, metric='euclidean'):
    """Compute exact pairwise distances."""
    d = scipy.spatial.distance.pdist(z, metric) # 得到100x100的距离矩阵。
    d = scipy.spatial.distance.squareform(d)
    # k-NN graph.
    idx = np.argsort(d)[:, 1:k+1] # 对列排序，找到前k个最小的节点序列。
    d.sort()
    d = d[:, 1:k+1] #前k小的距离矩阵。
    return d, idx

def adjacency(dist, idx):
    """Return the adjacency matrix of a kNN graph."""
    M, k = dist.shape
    assert M, k == idx.shape
    assert dist.min() >= 0

    # Weights. 对距离进行处理。
    sigma2 = np.mean(dist[:, -1])**2
    dist = np.exp(- dist**2 / sigma2)

    # Weight matrix.
    I = np.arange(0, M).repeat(k)  # M X K  一共M个点。
    J = idx.reshape(M*k) # 顶点编号就行排序。
    V = dist.reshape(M*k) # 相应的距离进行排序。
    W = scipy.sparse.coo_matrix((V, (I, J)), shape=(M, M))
    # W[I[k], J[k]] = v[k] ，一共M X K 个值，按照这种位置存放。

    # No self-connections.
    W.setdiag(0) # 对角为0

    # Non-directed graph.
    bigger = W.T > W
    W = W - W.multiply(bigger) + W.T.multiply(bigger) # 使矩阵对称。

    assert W.nnz % 2 == 0
    assert np.abs(W - W.T).mean() < 1e-10
    assert type(W) is scipy.sparse.csr.csr_matrix
    return W

# 以上两个函数一个是计算距离并返回最近的k个顶点的编号以及距离的值。
# adjacency 是用来从上一步得到距离和顶点编号来求邻接矩阵的A的。
dist, idx = graph.distance_scipy_spatial(X_train.T, k=10, metric='euclidean')
# 计算特征之间的距离。
A = graph.adjacency(dist, idx).astype(np.float32)

assert A.shape == (d, d)
print('d = |V| = {}, k|V| < |E| = {}'.format(d, A.nnz)) # 返回顶点的数量和邻接矩阵非0值。
# d = |V| = 100, k|V| < |E| = 1324
# plt.spy(A, markersize=2, color='black')
# plt.show()

### step3 ### step3 ### step3 ### step3 ### step3 ### step3 ### step3 ### step3
# 粗化处理，因为需要进行池化操作，为了实现论文中的方法，需要进行粗化和排序，添加
# 伪节点。
# 粗化函数 coarsen :
import numpy as np
import scipy.sparse

# 粗化的函数。
def coarsen(A, levels, self_connections=False):
    """
    Coarsen a graph, represented by its adjacency matrix A, at multiple
    levels.
    """
    graphs, parents = metis(A, levels) # metis方法进行粗化。
    perms = compute_perm(parents)

    for i, A in enumerate(graphs):
        M, M = A.shape

        if not self_connections:
            A = A.tocoo()
            A.setdiag(0)

        if i < levels:
            A = perm_adjacency(A, perms[i])

        A = A.tocsr()
        A.eliminate_zeros()
        graphs[i] = A

        Mnew, Mnew = A.shape
        print('Layer {0}: M_{0} = |V| = {1} nodes ({2} added),'
              '|E| = {3} edges'.format(i, Mnew, Mnew-M, A.nnz//2))

    return graphs, perms[0] if levels > 0 else None


def metis(W, levels, rid=None):
    """
    Coarsen a graph multiple times using the METIS algorithm.

    INPUT
    W: symmetric sparse weight (adjacency) matrix
    levels: the number of coarsened graphs

    OUTPUT
    graph[0]: original graph of size N_1
    graph[2]: coarser graph of size N_2 < N_1
    graph[levels]: coarsest graph of Size N_levels < ... < N_2 < N_1
    parents[i] is a vector of size N_i with entries ranging from 1 to N_{i+1}
        which indicate the parents in the coarser graph[i+1]
    nd_sz{i} is a vector of size N_i that contains the size of the supernode in the graph{i}

    NOTE
    if "graph" is a list of length k, then "parents" will be a list of length k-1
    """

    N, N = W.shape #邻接矩阵
    if rid is None:
        rid = np.random.permutation(range(N))  # 随机打乱N个节点的次序。
    parents = []
    degree = W.sum(axis=0) - W.diagonal()
    graphs = []
    graphs.append(W)
    #supernode_size = np.ones(N)
    #nd_sz = [supernode_size]
    #count = 0

    #while N > maxsize:
    for _ in range(levels):

        #count += 1

        # CHOOSE THE WEIGHTS FOR THE PAIRING
        # weights = ones(N,1)       # metis weights
        weights = degree            # graclus weights
        # weights = supernode_size  # other possibility
        weights = np.array(weights).squeeze()

        # PAIR THE VERTICES AND CONSTRUCT THE ROOT VECTOR
        idx_row, idx_col, val = scipy.sparse.find(W) # 非零元素的索引和值。
        perm = np.argsort(idx_row)   #对行索引进行排序。
        rr = idx_row[perm]
        cc = idx_col[perm]  # rr cc 就是非零元素的坐标。
        vv = val[perm]  # 相应的值。
        cluster_id = metis_one_level(rr,cc,vv,rid,weights)  # rr is ordered
        parents.append(cluster_id)

        # COMPUTE THE EDGES WEIGHTS FOR THE NEW GRAPH
        nrr = cluster_id[rr]   #新的图的rr，cc ，将原来的相应的节点用聚类编号代替。
        ncc = cluster_id[cc]   #也就是减少了一半。
        nvv = vv
        Nnew = cluster_id.max() + 1
        # CSR is more appropriate: row,val pairs appear multiple times
        W = scipy.sparse.csr_matrix((nvv,(nrr,ncc)), shape=(Nnew,Nnew))  #新图的邻接矩阵。
        # W(nrr(k), ncc(k)) = nvv(k)
        W.eliminate_zeros()
        # Add new graph to the list of all coarsened graphs
        graphs.append(W)
        N, N = W.shape

        # COMPUTE THE DEGREE (OMIT OR NOT SELF LOOPS)
        degree = W.sum(axis=0)

        ss = np.array(W.sum(axis=0)).squeeze()  #度的列表。
        rid = np.argsort(ss) # 子图需要排序。

    return graphs, parents # 粗化的图和每一个图中结点对应的聚类列表。

# Coarsen a graph given by rr,cc,vv.  rr is assumed to be ordered
def metis_one_level(rr,cc,vv,rid,weights):
    '''进行一次粗化，返回的是粗化的节点的粗化编号（父节点编号）'''
    nnz = rr.shape[0]
    N = rr[nnz-1] + 1  # rr[nnz-1] 的值最大行索引，也就是节点数量。

    marked = np.zeros(N, np.bool) # 是否聚类过的标记。
    rowstart = np.zeros(N, np.int32) # 开始位置？？。
    rowlength = np.zeros(N, np.int32) # 长度。
    cluster_id = np.zeros(N, np.int32) #聚类选择的点？？

    oldval = rr[0]
    count = 0
    clustercount = 0

    #
    for ii in range(nnz):
        rowlength[count] = rowlength[count] + 1 #统计N个结点的度也就是长度。
        if rr[ii] > oldval: #判断是否换了结点。
            oldval = rr[ii]
            rowstart[count+1] = ii #每个节点开始的索引。
            count = count + 1

    for ii in range(N):
        tid = rid[ii] # 打乱的N个节点。0 - N-1
        if not marked[tid]: #默认都是没有被聚类的。
            wmax = 0.0 # 最大的权重。
            rs = rowstart[tid] #边开始的位置。
            marked[tid] = True
            bestneighbor = -1
            for jj in range(rowlength[tid]): #行的非零元素的长度。
                nid = cc[rs+jj] # 另一个点的索引。开始的索引+长度就是所有的边，用它找出对应的节点的索引。
                # 判断这个节点是否被标记过了。

                # 计算该聚类的点。
                if marked[nid]: # 已经被标记了。
                    tval = 0.0
                else:
                    tval = vv[rs+jj] * (1.0/weights[tid] + 1.0/weights[nid])

                if tval > wmax:
                    wmax = tval
                    bestneighbor = nid  # 找出聚类的点。

            cluster_id[tid] = clustercount # 聚类编号。从0开始排。

            if bestneighbor > -1:
                cluster_id[bestneighbor] = clustercount #对应的那个点，也是同样的聚类编号。
                marked[bestneighbor] = True #并且标记成已聚类。

            clustercount += 1

    return cluster_id # N个点的聚类编号列表。

graphs, perm = coarsening.coarsen(A, levels=3, self_connections=False)
# plt.spy(graphs[3], markersize=2, color='black')
# plt.show() # 查看粗化的结果。

以上是数据预处理和使用部分代码。
GNN 部分代码：

基类：

class base_model(object):
    
    def __init__(self):
        self.regularizers = []
    
    # High-level interface which runs the constructed computational graph.
    
    def predict(self, data, labels=None, sess=None):
        loss = 0
        size = data.shape[0]
        predictions = np.empty(size)
        sess = self._get_session(sess)
        for begin in range(0, size, self.batch_size):
            end = begin + self.batch_size
            end = min([end, size])
            
            batch_data = np.zeros((self.batch_size, data.shape[1]))
            tmp_data = data[begin:end,:]
            if type(tmp_data) is not np.ndarray:
                tmp_data = tmp_data.toarray()  # convert sparse matrices
            batch_data[:end-begin] = tmp_data
            feed_dict = {self.ph_data: batch_data, self.ph_dropout: 1}
            
            # Compute loss if labels are given.
            if labels is not None:
                batch_labels = np.zeros(self.batch_size)
                batch_labels[:end-begin] = labels[begin:end]
                feed_dict[self.ph_labels] = batch_labels
                batch_pred, batch_loss = sess.run([self.op_prediction, self.op_loss], feed_dict)
                loss += batch_loss
            else:
                batch_pred = sess.run(self.op_prediction, feed_dict)
            
            predictions[begin:end] = batch_pred[:end-begin]
            
        if labels is not None:
            return predictions, loss * self.batch_size / size
        else:
            return predictions
        
    def evaluate(self, data, labels, sess=None):
        """
        Runs one evaluation against the full epoch of data.
        Return the precision and the number of correct predictions.
        Batch evaluation saves memory and enables this to run on smaller GPUs.

        sess: the session in which the model has been trained.
        op: the Tensor that returns the number of correct predictions.
        data: size N x M
            N: number of signals (samples)
            M: number of vertices (features)
        labels: size N
            N: number of signals (samples)
        """
        t_process, t_wall = time.process_time(), time.time()
        predictions, loss = self.predict(data, labels, sess)
        #print(predictions)
        ncorrects = sum(predictions == labels)
        accuracy = 100 * sklearn.metrics.accuracy_score(labels, predictions)
        f1 = 100 * sklearn.metrics.f1_score(labels, predictions, average='weighted')
        string = 'accuracy: {:.2f} ({:d} / {:d}), f1 (weighted): {:.2f}, loss: {:.2e}'.format(
                accuracy, ncorrects, len(labels), f1, loss)
        if sess is None:
            string += '\ntime: {:.0f}s (wall {:.0f}s)'.format(time.process_time()-t_process, time.time()-t_wall)
        return string, accuracy, f1, loss

    def fit(self, train_data, train_labels, val_data, val_labels):
        t_process, t_wall = time.process_time(), time.time()
        sess = tf.Session(graph=self.graph)  # 调用图。
        shutil.rmtree(self._get_path('summaries'), ignore_errors=True)
        writer = tf.summary.FileWriter(self._get_path('summaries'), self.graph)
        shutil.rmtree(self._get_path('checkpoints'), ignore_errors=True)
        os.makedirs(self._get_path('checkpoints'))
        path = os.path.join(self._get_path('checkpoints'), 'model')
        sess.run(self.op_init) # 初始化。

        # Training.
        accuracies = []
        losses = []
        indices = collections.deque()
        num_steps = int(self.num_epochs * train_data.shape[0] / self.batch_size)
        for step in range(1, num_steps+1):

            # Be sure to have used all the samples before using one a second time.
            if len(indices) < self.batch_size:
                indices.extend(np.random.permutation(train_data.shape[0]))
            idx = [indices.popleft() for i in range(self.batch_size)]

            batch_data, batch_labels = train_data[idx,:], train_labels[idx]
            if type(batch_data) is not np.ndarray:
                batch_data = batch_data.toarray()  # convert sparse matrices
            feed_dict = {self.ph_data: batch_data, self.ph_labels: batch_labels, self.ph_dropout: self.dropout}
            learning_rate, loss_average = sess.run([self.op_train, self.op_loss_average], feed_dict)

            # Periodical evaluation of the model.
            if step % self.eval_frequency == 0 or step == num_steps:
                epoch = step * self.batch_size / train_data.shape[0]
                print('step {} / {} (epoch {:.2f} / {}):'.format(step, num_steps, epoch, self.num_epochs))
                print('  learning_rate = {:.2e}, loss_average = {:.2e}'.format(learning_rate, loss_average))
                string, accuracy, f1, loss = self.evaluate(val_data, val_labels, sess)
                accuracies.append(accuracy)
                losses.append(loss)
                print('  validation {}'.format(string))
                print('  time: {:.0f}s (wall {:.0f}s)'.format(time.process_time()-t_process, time.time()-t_wall))

                # Summaries for TensorBoard.
                summary = tf.Summary()
                summary.ParseFromString(sess.run(self.op_summary, feed_dict))
                summary.value.add(tag='validation/accuracy', simple_value=accuracy)
                summary.value.add(tag='validation/f1', simple_value=f1)
                summary.value.add(tag='validation/loss', simple_value=loss)
                writer.add_summary(summary, step)
                
                # Save model parameters (for evaluation).
                self.op_saver.save(sess, path, global_step=step)

        print('validation accuracy: peak = {:.2f}, mean = {:.2f}'.format(max(accuracies), np.mean(accuracies[-10:])))
        writer.close()
        sess.close()
        
        t_step = (time.time() - t_wall) / num_steps
        return accuracies, losses, t_step

    def get_var(self, name):
        sess = self._get_session()
        var = self.graph.get_tensor_by_name(name + ':0')
        val = sess.run(var)
        sess.close()
        return val

    # Methods to construct the computational graph.
    def build_graph(self, M_0):
        """Build the computational graph of the model."""
        self.graph = tf.Graph()
        with self.graph.as_default():
            # Define operations and tensors in `self.graph`.
            # 添加tensor和操作到计算图中。
            # Inputs.
            with tf.name_scope('inputs'):
                self.ph_data = tf.placeholder(tf.float32, (self.batch_size, M_0), 'data')
                self.ph_labels = tf.placeholder(tf.int32, (self.batch_size), 'labels')
                self.ph_dropout = tf.placeholder(tf.float32, (), 'dropout')

            # Model.
            op_logits = self.inference(self.ph_data, self.ph_dropout)  # 相当于前向传播。
            # 等于是建立了图。
            # 定义操作。
            self.op_loss, self.op_loss_average = self.loss(op_logits, self.ph_labels, self.regularization)
            self.op_train = self.training(self.op_loss, self.learning_rate,
                    self.decay_steps, self.decay_rate, self.momentum) # 进行训练，返回当前学习率。
            self.op_prediction = self.prediction(op_logits)

            # Initialize variables, i.e. weights and biases.
            self.op_init = tf.global_variables_initializer()  # 初始化参数。
            
            # Summaries for TensorBoard and Save for model parameters.
            self.op_summary = tf.summary.merge_all()
            self.op_saver = tf.train.Saver(max_to_keep=5)
        
        self.graph.finalize()   # 完成建图，保证整个图没有新的操作加进去。
    
    def inference(self, data, dropout):
        """
        It builds the model, i.e. the computational graph, as far as
        is required for running the network forward to make predictions,
        i.e. return logits given raw data.

        data: size N x M
            N: number of signals (samples)
            M: number of vertices (features)
        training: we may want to discriminate the two, e.g. for dropout.
            True: the model is built for training.
            False: the model is built for evaluation.
        """
        # TODO: optimizations for sparse data
        logits = self._inference(data, dropout)
        return logits
    
    def probabilities(self, logits):
        """Return the probability of a sample to belong to each class."""
        with tf.name_scope('probabilities'):
            probabilities = tf.nn.softmax(logits)
            return probabilities

    def prediction(self, logits):
        """Return the predicted classes."""
        with tf.name_scope('prediction'):
            prediction = tf.argmax(logits, axis=1)
            return prediction

    def loss(self, logits, labels, regularization):
        """Adds to the inference model the layers required to generate loss."""
        with tf.name_scope('loss'):
            with tf.name_scope('cross_entropy'):
                labels = tf.to_int64(labels)
                cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=labels)
                cross_entropy = tf.reduce_mean(cross_entropy) #均值损失
            with tf.name_scope('regularization'):
                regularization *= tf.add_n(self.regularizers)  #规范
            loss = cross_entropy + regularization
            
            # Summaries for TensorBoard.生成摘要。
            tf.summary.scalar('loss/cross_entropy', cross_entropy)
            tf.summary.scalar('loss/regularization', regularization)
            tf.summary.scalar('loss/total', loss)
            with tf.name_scope('averages'): #求均值。
                averages = tf.train.ExponentialMovingAverage(0.9)  #指数移动平均。
                op_averages = averages.apply([cross_entropy, regularization, loss])
                # 求平均值。
                tf.summary.scalar('loss/avg/cross_entropy', averages.average(cross_entropy))
                tf.summary.scalar('loss/avg/regularization', averages.average(regularization))
                tf.summary.scalar('loss/avg/total', averages.average(loss))
                with tf.control_dependencies([op_averages]):
                    loss_average = tf.identity(averages.average(loss), name='control')
            return loss, loss_average
    
    def training(self, loss, learning_rate, decay_steps, decay_rate=0.95, momentum=0.9):
        """Adds to the loss model the Ops required to generate and apply gradients."""
        with tf.name_scope('training'):
            # Learning rate.
            global_step = tf.Variable(0, name='global_step', trainable=False)
            if decay_rate != 1:
                learning_rate = tf.train.exponential_decay(
                        learning_rate, global_step, decay_steps, decay_rate, staircase=True)
            tf.summary.scalar('learning_rate', learning_rate)
            # Optimizer.
            if momentum == 0:
                optimizer = tf.train.GradientDescentOptimizer(learning_rate)
                #optimizer = tf.train.AdamOptimizer(learning_rate=0.001)
            else:
                optimizer = tf.train.MomentumOptimizer(learning_rate, momentum) # 优化器。
            grads = optimizer.compute_gradients(loss) #计算梯度。
            op_gradients = optimizer.apply_gradients(grads, global_step=global_step) # 更新权重。
            # Histograms.
            for grad, var in grads:
                if grad is None:
                    print('warning: {} has no gradient'.format(var.op.name))
                else:
                    tf.summary.histogram(var.op.name + '/gradients', grad)
            # The op return the learning rate.
            with tf.control_dependencies([op_gradients]):
                op_train = tf.identity(learning_rate, name='control')
            return op_train

    # Helper methods.

    def _get_path(self, folder):
        path = os.path.dirname(os.path.realpath(__file__))
        return os.path.join(path, '..', folder, self.dir_name)

    def _get_session(self, sess=None):
        """Restore parameters if no session given."""
        if sess is None:
            sess = tf.Session(graph=self.graph)
            filename = tf.train.latest_checkpoint(self._get_path('checkpoints'))
            self.op_saver.restore(sess, filename)
        return sess

    def _weight_variable(self, shape, regularization=True):
        initial = tf.truncated_normal_initializer(0, 0.1)
        var = tf.get_variable('weights', shape, tf.float32, initializer=initial)
        if regularization:
            self.regularizers.append(tf.nn.l2_loss(var))
        tf.summary.histogram(var.op.name, var)
        return var

    def _bias_variable(self, shape, regularization=True):
        initial = tf.constant_initializer(0.1)
        var = tf.get_variable('bias', shape, tf.float32, initializer=initial)
        if regularization:
            self.regularizers.append(tf.nn.l2_loss(var))
        tf.summary.histogram(var.op.name, var)
        return var

    def _conv2d(self, x, W):
        return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

gnn:

class cgcnn(base_model):
    """
    Graph CNN which uses the Chebyshev approximation.

    The following are hyper-parameters of graph convolutional layers.
    They are lists, which length is equal to the number of gconv layers.
        F: Number of features.
        K: List of polynomial orders, i.e. filter sizes or number of hopes.
        p: Pooling size.
           Should be 1 (no pooling) or a power of 2 (reduction by 2 at each coarser level).
           Beware to have coarsened enough.

    L: List of Graph Laplacians. Size M x M. One per coarsening level.

    The following are hyper-parameters of fully connected layers.
    They are lists, which length is equal to the number of fc layers.
        M: Number of features per sample, i.e. number of hidden neurons.
           The last layer is the softmax, i.e. M[-1] is the number of classes.
    
    The following are choices of implementation for various blocks.
        filter: filtering operation, e.g. chebyshev5, lanczos2 etc.
        brelu: bias and relu, e.g. b1relu or b2relu.
        pool: pooling, e.g. mpool1.
    
    Training parameters:
        num_epochs:    Number of training epochs.
        learning_rate: Initial learning rate.
        decay_rate:    Base of exponential decay. No decay with 1.
        decay_steps:   Number of steps after which the learning rate decays.
        momentum:      Momentum. 0 indicates no momentum.

    Regularization parameters:
        regularization: L2 regularizations of weights and biases.
        dropout:        Dropout (fc layers): probability to keep hidden neurons. No dropout with 1.
        batch_size:     Batch size. Must divide evenly into the dataset sizes.
        eval_frequency: Number of steps between evaluations.

    Directories:
        dir_name: Name for directories (summaries and model parameters).
    """
    def __init__(self, L, F, K, p, M, filter='chebyshev5', brelu='b1relu', pool='mpool1',
                num_epochs=20, learning_rate=0.1, decay_rate=0.95, decay_steps=None, momentum=0.9,
                regularization=0, dropout=0, batch_size=100, eval_frequency=200,
                dir_name=''):
        super().__init__()
        
        # Verify the consistency w.r.t. the number of layers.
        assert len(L) >= len(F) == len(K) == len(p)  # 每一层的拉普拉斯，parent。。。。
        assert np.all(np.array(p) >= 1)
        p_log2 = np.where(np.array(p) > 1, np.log2(p), 0)
        assert np.all(np.mod(p_log2, 1) == 0)  # Powers of 2.
        assert len(L) >= 1 + np.sum(p_log2)  # Enough coarsening levels for pool sizes.
        
        # Keep the useful Laplacians only. May be zero.
        M_0 = L[0].shape[0]
        j = 0
        self.L = []
        for pp in p:
            self.L.append(L[j])
            j += int(np.log2(pp)) if pp > 1 else 0
        L = self.L
        
        # Print information about NN architecture.
        Ngconv = len(p) # 卷积层数。
        Nfc = len(M)
        print('NN architecture')
        print('  input: M_0 = {}'.format(M_0))
        for i in range(Ngconv):
            print('  layer {0}: cgconv{0}'.format(i+1))
            print('    representation: M_{0} * F_{1} / p_{1} = {2} * {3} / {4} = {5}'.format(
                    i, i+1, L[i].shape[0], F[i], p[i], L[i].shape[0]*F[i]//p[i]))
            F_last = F[i-1] if i > 0 else 1
            print('    weights: F_{0} * F_{1} * K_{1} = {2} * {3} * {4} = {5}'.format(
                    i, i+1, F_last, F[i], K[i], F_last*F[i]*K[i]))
            if brelu == 'b1relu':
                print('    biases: F_{} = {}'.format(i+1, F[i]))
            elif brelu == 'b2relu':
                print('    biases: M_{0} * F_{0} = {1} * {2} = {3}'.format(
                        i+1, L[i].shape[0], F[i], L[i].shape[0]*F[i]))
        for i in range(Nfc):
            name = 'logits (softmax)' if i == Nfc-1 else 'fc{}'.format(i+1)
            print('  layer {}: {}'.format(Ngconv+i+1, name))
            print('    representation: M_{} = {}'.format(Ngconv+i+1, M[i]))
            M_last = M[i-1] if i > 0 else M_0 if Ngconv == 0 else L[-1].shape[0] * F[-1] // p[-1]
            print('    weights: M_{} * M_{} = {} * {} = {}'.format(
                    Ngconv+i, Ngconv+i+1, M_last, M[i], M_last*M[i]))
            print('    biases: M_{} = {}'.format(Ngconv+i+1, M[i]))
        
        # Store attributes and bind operations.
        self.L, self.F, self.K, self.p, self.M = L, F, K, p, M
        self.num_epochs, self.learning_rate = num_epochs, learning_rate
        self.decay_rate, self.decay_steps, self.momentum = decay_rate, decay_steps, momentum
        self.regularization, self.dropout = regularization, dropout
        self.batch_size, self.eval_frequency = batch_size, eval_frequency
        self.dir_name = dir_name
        self.filter = getattr(self, filter)
        self.brelu = getattr(self, brelu)
        self.pool = getattr(self, pool)
        
        # Build the computational graph.
        self.build_graph(M_0)
        
    def filter_in_fourier(self, x, L, Fout, K, U, W):
        # TODO: N x F x M would avoid the permutations
        N, M, Fin = x.get_shape()
        N, M, Fin = int(N), int(M), int(Fin)
        x = tf.transpose(x, perm=[1, 2, 0])  # M x Fin x N
        # Transform to Fourier domain
        x = tf.reshape(x, [M, Fin*N])  # M x Fin*N
        x = tf.matmul(U, x)  # M x Fin*N
        x = tf.reshape(x, [M, Fin, N])  # M x Fin x N
        # Filter
        x = tf.matmul(W, x)  # for each feature
        x = tf.transpose(x)  # N x Fout x M
        x = tf.reshape(x, [N*Fout, M])  # N*Fout x M
        # Transform back to graph domain
        x = tf.matmul(x, U)  # N*Fout x M
        x = tf.reshape(x, [N, Fout, M])  # N x Fout x M
        return tf.transpose(x, perm=[0, 2, 1])  # N x M x Fout

    def fourier(self, x, L, Fout, K):
        assert K == L.shape[0]  # artificial but useful to compute number of parameters
        N, M, Fin = x.get_shape()
        N, M, Fin = int(N), int(M), int(Fin)
        # Fourier basis
        _, U = graph.fourier(L)
        U = tf.constant(U.T, dtype=tf.float32)
        # Weights
        W = self._weight_variable([M, Fout, Fin], regularization=False)
        return self.filter_in_fourier(x, L, Fout, K, U, W)

    def spline(self, x, L, Fout, K):
        N, M, Fin = x.get_shape()
        N, M, Fin = int(N), int(M), int(Fin)
        # Fourier basis
        lamb, U = graph.fourier(L)
        U = tf.constant(U.T, dtype=tf.float32)  # M x M
        # Spline basis
        B = bspline_basis(K, lamb, degree=3)  # M x K
        #B = bspline_basis(K, len(lamb), degree=3)  # M x K
        B = tf.constant(B, dtype=tf.float32)
        # Weights
        W = self._weight_variable([K, Fout*Fin], regularization=False)
        W = tf.matmul(B, W)  # M x Fout*Fin
        W = tf.reshape(W, [M, Fout, Fin])
        return self.filter_in_fourier(x, L, Fout, K, U, W)

    def chebyshev2(self, x, L, Fout, K):
        """
        Filtering with Chebyshev interpolation
        Implementation: numpy.
        
        Data: x of size N x M x F
            N: number of signals
            M: number of vertices
            F: number of features per signal per vertex # 也就是输入通道数。
        """
        N, M, Fin = x.get_shape()
        N, M, Fin = int(N), int(M), int(Fin)
        # Rescale Laplacian. Copy to not modify the shared L.
        L = scipy.sparse.csr_matrix(L)
        L = graph.rescale_L(L, lmax=2)
        # Transform to Chebyshev basis
        x = tf.transpose(x, perm=[1, 2, 0])  # M x Fin x N
        x = tf.reshape(x, [M, Fin*N])  # M x Fin*N
        def chebyshev(x):
            return graph.chebyshev(L, x, K)
        x = tf.py_func(chebyshev, [x], [tf.float32])[0]  # K x M x Fin*N
        x = tf.reshape(x, [K, M, Fin, N])  # K x M x Fin x N
        x = tf.transpose(x, perm=[3,1,2,0])  # N x M x Fin x K
        x = tf.reshape(x, [N*M, Fin*K])  # N*M x Fin*K
        # Filter: Fin*Fout filters of order K, i.e. one filterbank per feature.
        W = self._weight_variable([Fin*K, Fout], regularization=False)
        x = tf.matmul(x, W)  # N*M x Fout
        return tf.reshape(x, [N, M, Fout])  # N x M x Fout

    def chebyshev5(self, x, L, Fout, K):
        N, M, Fin = x.get_shape()
        N, M, Fin = int(N), int(M), int(Fin)
        # Rescale Laplacian and store as a TF sparse tensor. Copy to not modify the shared L.
        L = scipy.sparse.csr_matrix(L)
        L = graph.rescale_L(L, lmax=2)
        L = L.tocoo()
        indices = np.column_stack((L.row, L.col))
        L = tf.SparseTensor(indices, L.data, L.shape)
        L = tf.sparse_reorder(L)
        # Transform to Chebyshev basis
        x0 = tf.transpose(x, perm=[1, 2, 0])  # M x Fin x N
        x0 = tf.reshape(x0, [M, Fin*N])  # M x Fin*N
        x = tf.expand_dims(x0, 0)  # 1 x M x Fin*N
        def concat(x, x_):
            x_ = tf.expand_dims(x_, 0)  # 1 x M x Fin*N
            return tf.concat([x, x_], axis=0)  # K x M x Fin*N
        if K > 1:
            x1 = tf.sparse_tensor_dense_matmul(L, x0)
            x = concat(x, x1)
        for k in range(2, K):
            x2 = 2 * tf.sparse_tensor_dense_matmul(L, x1) - x0  # M x Fin*N
            x = concat(x, x2)
            x0, x1 = x1, x2
        x = tf.reshape(x, [K, M, Fin, N])  # K x M x Fin x N
        x = tf.transpose(x, perm=[3,1,2,0])  # N x M x Fin x K
        x = tf.reshape(x, [N*M, Fin*K])  # N*M x Fin*K
        # Filter: Fin*Fout filters of order K, i.e. one filterbank per feature pair.
        W = self._weight_variable([Fin*K, Fout], regularization=False)
        x = tf.matmul(x, W)  # N*M x Fout
        return tf.reshape(x, [N, M, Fout])  # N x M x Fout

    def b1relu(self, x):
        """Bias and ReLU. One bias per filter."""
        N, M, F = x.get_shape()
        b = self._bias_variable([1, 1, int(F)], regularization=False)
        return tf.nn.relu(x + b)

    def b2relu(self, x):
        """Bias and ReLU. One bias per vertex per filter."""
        N, M, F = x.get_shape()
        b = self._bias_variable([1, int(M), int(F)], regularization=False)
        return tf.nn.relu(x + b)

    def mpool1(self, x, p):
        """Max pooling of size p. Should be a power of 2."""
        if p > 1:
            x = tf.expand_dims(x, 3)  # N x M x F x 1
            x = tf.nn.max_pool(x, ksize=[1,p,1,1], strides=[1,p,1,1], padding='SAME')
            #tf.maximum
            return tf.squeeze(x, [3])  # N x M/p x F
        else:
            return x

    def apool1(self, x, p):
        """Average pooling of size p. Should be a power of 2."""
        if p > 1:
            x = tf.expand_dims(x, 3)  # N x M x F x 1
            x = tf.nn.avg_pool(x, ksize=[1,p,1,1], strides=[1,p,1,1], padding='SAME')
            return tf.squeeze(x, [3])  # N x M/p x F
        else:
            return x

    def fc(self, x, Mout, relu=True):
        """Fully connected layer with Mout features."""
        N, Min = x.get_shape()
        W = self._weight_variable([int(Min), Mout], regularization=True)
        b = self._bias_variable([Mout], regularization=True)
        x = tf.matmul(x, W) + b
        return tf.nn.relu(x) if relu else x

    def _inference(self, x, dropout):
        # Graph convolutional layers.
        x = tf.expand_dims(x, 2)  # N x M x F=1
        for i in range(len(self.p)):
            with tf.variable_scope('conv{}'.format(i+1)):
                with tf.name_scope('filter'):
                    x = self.filter(x, self.L[i], self.F[i], self.K[i])  # 这一步其实就完成了？？？？
                    # 卷积完成。
                with tf.name_scope('bias_relu'):
                    x = self.brelu(x)
                    # 激活完成。
                with tf.name_scope('pooling'):
                    x = self.pool(x, self.p[i])  # p 每次 都是2 ???
                    # 池化完成。
                    # 循环len(layers) 次。
        
        # Fully connected hidden layers.
        N, M, F = x.get_shape()  # 输入为batch，顶点数， 通道数。也就是每个顶点数据的维度。
        x = tf.reshape(x, [int(N), int(M*F)])  # N x M
        for i,M in enumerate(self.M[:-1]): # 最后几层全连接？
            with tf.variable_scope('fc{}'.format(i+1)):
                x = self.fc(x, M)
                x = tf.nn.dropout(x, dropout)
        
        # Logits linear layer, i.e. softmax without normalization.
        with tf.variable_scope('logits'):
            x = self.fc(x, self.M[-1], relu=False)
        return x