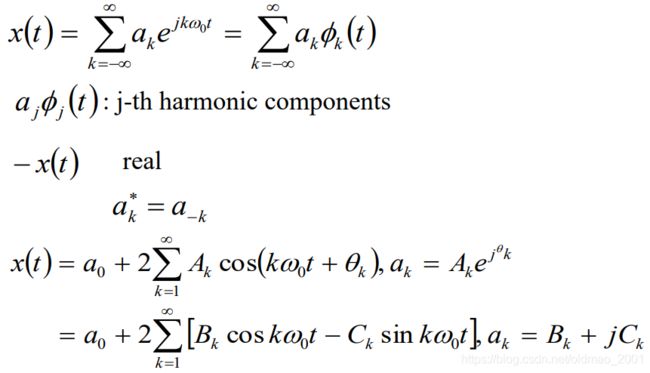番外.李宏毅学习笔记.12.GNN

前言

2020版加了一些内容，补充进来
这课是貌似是TA姜成翰讲的Graph Neural Networks
这个玩意最近挺热，基于GNN做知识图谱还有推荐系统效果貌似不错。
公式输入请参考：在线Latex公式
GNN的公共库：https://www.dgl.ai/

Introduction

GNN可以分为两部分

NN（略）

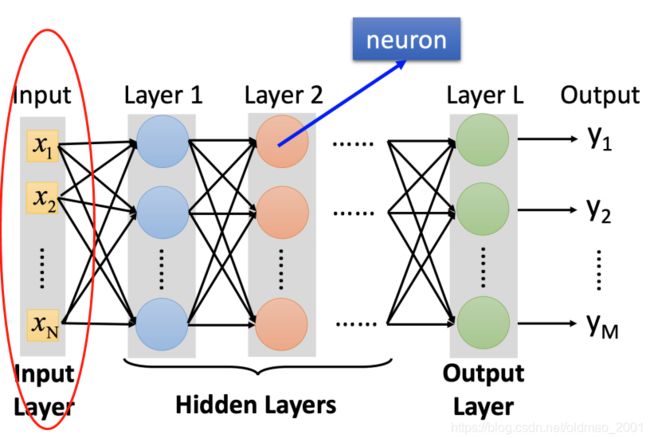
NN这块就列举了FC、CNN、RNN。以及时下最潮的变形金刚。
图这课主要举了几个例子

Graph

普通的树

化学

蛋白质表达

地铁

现在要思考的是如何把图按原来NN的思路进行输入？
就是把

变成：

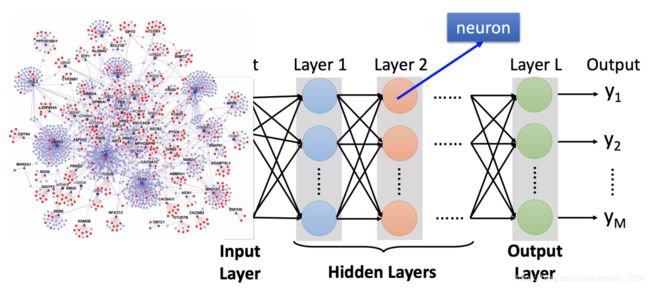
这先挖坑，后面再讲。

常见GNN应用

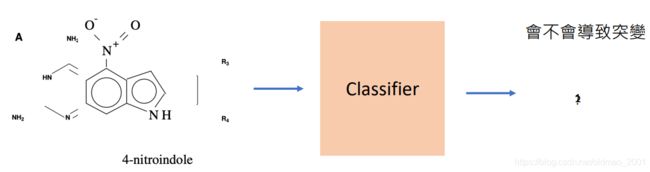
Classification

Generation

新冠靶向药的开发。
在生成的过程中可以加入很多constraint，例如：是新药，比较好合成，有效性等。

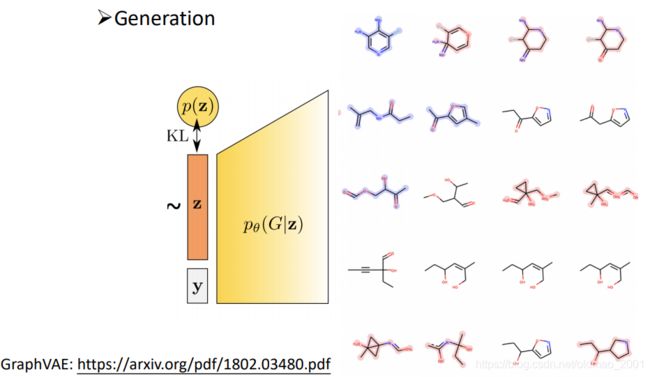
https://arxiv.org/pdf/1802.03480.pdf

结合社交网络的分类

现有数据：某烧脑侦探剧，用GNN来分类谁是凶手，输入可以是这些人的属性：姓名、性别职业什么的。

训练的模型可以干这个事情：

当然这是不够的，可以结合人物（实体）之间的关系来辅助分类，这个就是GNN的范畴。

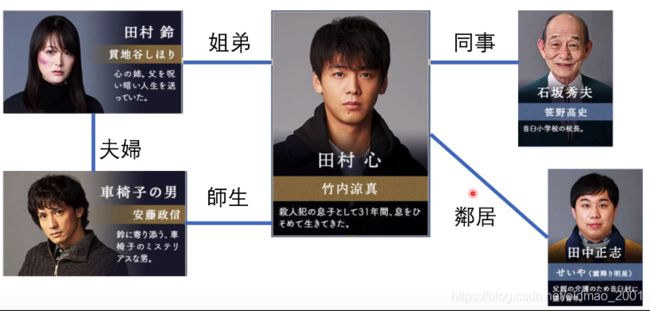
现有问题

1.How do we utilize the structures and relationship to help our model?关系杂
2.What if the graph is larger, like 20k nodes?模型大
3.What if we don‘t have the all the labels?无标签
看下面一个例子来理解，现有这样一个图结构：

蓝色是Unlabeled Node，褐色是Labeled Node
现在要推断黄圈中的节点的标签。
思想是A node can learn the structure from its neighbors（近朱者赤，近墨者黑）, but how?

借鉴CNN中的卷积操作，假设有6 x 6 image with 3 x 3 kernel

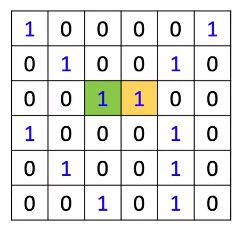
然后要对绿色和黄色的点进行特征提取，实际上是：


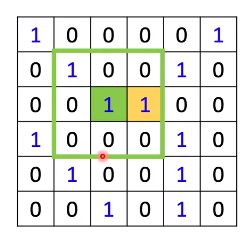
和filter相乘相加后就得到feature map。如何把卷积操作移植到Graph上？
Solution 1: Generalize the concept of convolution (corelation) to graph >> Spatial-based convolution
Solution 2: Back to the definition of convolution in signal processing>> Spectral-based convolution
第一种是把CNN的操作Generalize到GNN上。
第二种是借鉴信号处理中做法来进行卷积操作。

Roadmap

根据上面的两种Solutions，本次课程的内容如下：

Tasks, Dataset, and Benchmark

Tasks
ØSemi-supervised node classification
ØRegression
ØGraph classification
ØGraph representation learning
ØLink prediction
Common dataset
ØCORA: citation network. 2.7k nodes and 5.4k links
ØTU-MUTAG: 188 molecules with 18 nodes on average

Graph Classification: SuperPixel MNIST and CIFAR10

https://arxiv.org/pdf/2003.00982.pdf
先把图片转换为SuperPixel，然后再找出点之间的graph结构，进行识别

Regression: ZINC molecule graphs dataset

https://arxiv.org/pdf/1711.07553.pdf

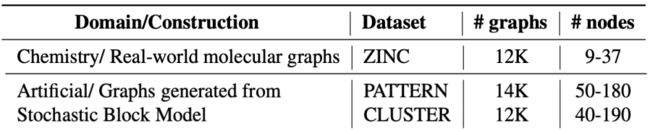
Node classification:Stochastic Block Model dataset

从已知的图结构，去找相似的pattern。左边
从图结构中做聚类。右边

Edge classification: Traveling Salesman Problem

将边进行分类，判断边是否属于最短路径中的边。

性能分析

不是层越多就是性能越好。
还可以用DropEdge得到类似抓爆的效果

Spatial-based GNN

这个是solution 1，因此是根据CNN的卷积进行移植：

要把下面的图中箭头所指的节点进行更新得到下一层的状态

注意上图中的箭头所指的节点是

Terminology:
ØAggregate: 用 neighbor feature update 下一层的 hidden state
ØReadout: 把所有 nodes 的 feature 集合起來代表整个 graph（类似LSTM把整个句子向量压缩为一个向量）

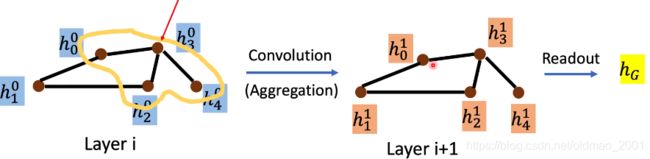
法1：NN4G (Neural Networks for Graph)09年

https://ieeexplore.ieee.org/document/4773279

然后，每个节点都做同样的操作：${\bar{w}}_i\cdot x_i$

下一层中，就把邻居的信息作为输入，更新到$v_3$，然后还要加上本身的信息。

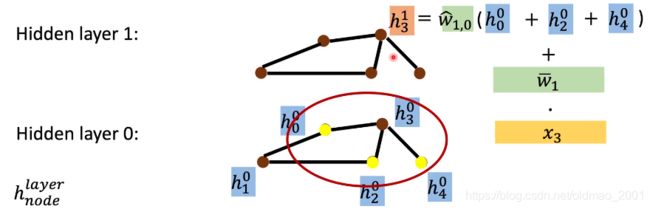
每层都计算完成后，进行Readout操作，每层都计算$X_i=MEAN(h^l)$，最后$y={\sum }_i^l{X}_i\cdot w_i$

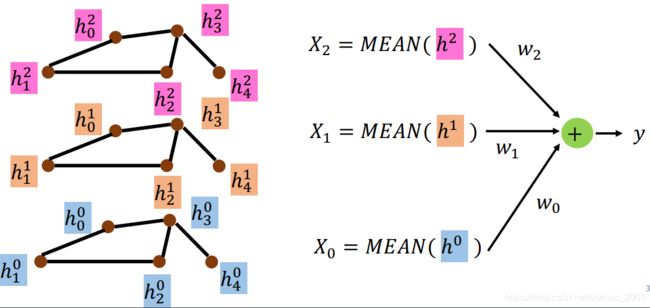
法2：DCNN (Diffusion-Convolution Neural Network )15年

https://arxiv.org/abs/1511.02136

第一层：

$$w_3^{0}MEAN(d(3,\cdot ))=1$$
上式表示把和第三个节点距离为1的节点加起来取平均，然后点乘$w_3^0$
第二层：

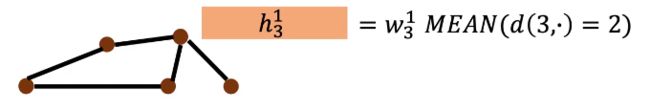
表示把和第三个节点距离为3的节点加起来取平均，然后点乘$w_3^1$，每个节点都做这个事情：

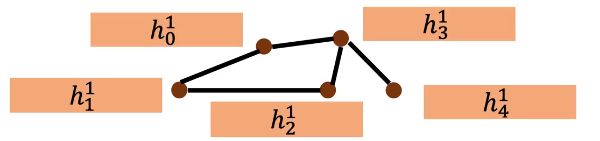
然后把每层的每个节点特征$h_i^l$堆叠起来得到$H^l$

每个节点的特征计算就把节点i对应的$h_i^l$从堆叠结果中提取出来，然后点乘w即可。

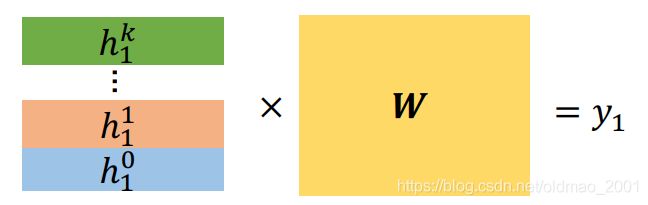
法3：MoNET (Mixture Model Networks)16年

https://arxiv.org/pdf/1611.08402.pdf
上面两个方法在处理节点和节点之间的关系的时候都是用加法，其实忽略节点之间如果边有权重，这样是不合理的，因此这个方法就是用来解决不同权重边的方法。
Define a measure on node ‘distances’
Use weighted sum (mean) instead of simply summing up (averaging) neighbor features.
具体做法如下：

$$u(x,y)=(\frac{1}{\sqrt{deg(x)}},\frac{1}{\sqrt{deg(y)}}{)}^T$$
其中$deg$代表节点的度，例如：节点3的度为3，节点0的度为2，因此$u(3,2)=(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{2}}{)}^T$
然后特征计算要根据下面公式来算：

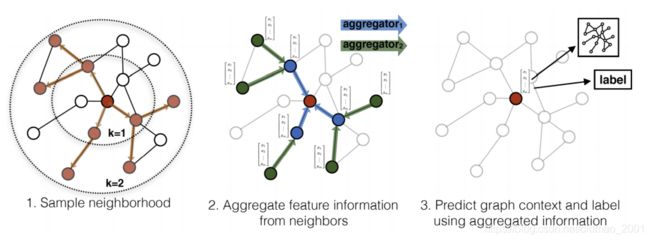
法4：GraphSAGE.18年

https://arxiv.org/pdf/1706.02216.pdf
SAmple and aggreGatE
Can work on both transductive and inductive setting
GraphSAGE learns how to embed node features from neighbors

这个方法在提取邻居信息上提出了三种方式：
AGGREGATION: mean, max-pooling, or LSTM

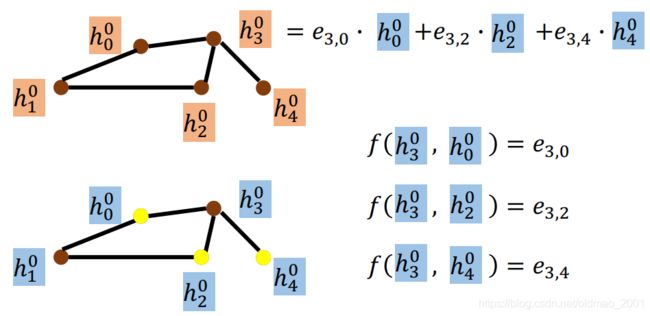
法5：GAT (Graph Attention Networks).18年

https://arxiv.org/pdf/1710.10903.pdf

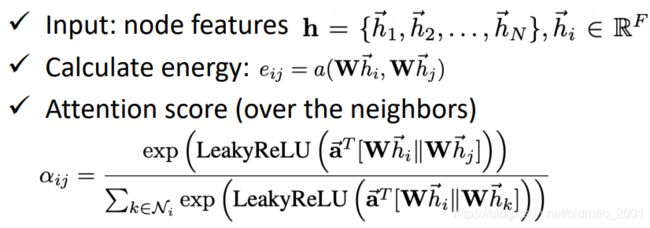
理论：GIN (Graph Isomorphism Network)

这个文章提供了证明什么方法是work的，什么方法是无用的。结论：

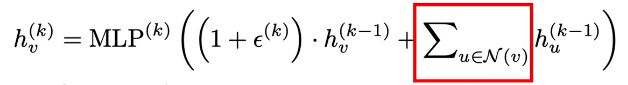
更新第k层第v个节点的时候要把它的邻居做求和，然后加上该节点与某个常数的乘积。这里提的是直接求和，不是求平均，也不是做maxpooling。为什么？
情况一，如果节点v的邻居都一样，求平均的话无法区分下面两种不同图结构。

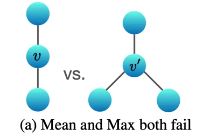
同理，还有下面两种情况：

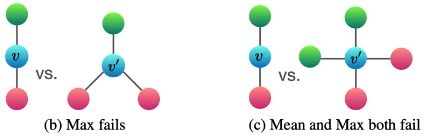
Graph Signal Processing and Spectral-based GNN

这节讲的是solution 2，就是用信号处理的方式来进行特征提取。之前讲过，直接对图中的节点做卷积是不行的，因为不能把节点的邻居和CNN中的卷积核位置一一对应，然后做运算，于是借鉴信号处理的方法，先用傅里叶变化分别处理节点和卷积核，然后相乘，然后再反傅里叶变化得到结果：

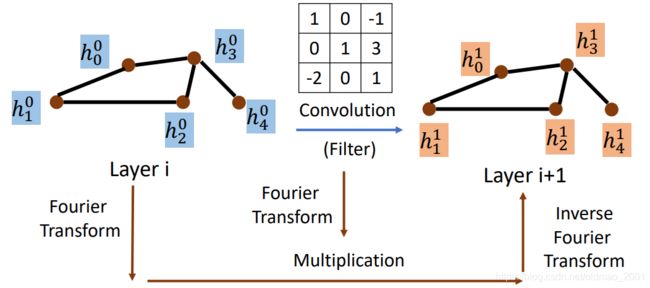
Warning of Signal And System（没看懂系列。。。）

一个信号可以看做是一个n维空间的向量，这个向量是由一组基向量合成的，下面这些TA都没解释清楚。。。

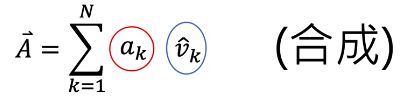
Fourier Series Representation

傅里叶级数：可以把某一个周期信号进行傅里叶展开

信号表示的两个域

可以从公式里面大概可以看出来，一个信号表示的原始形式可以经过一些变化得到另外一种表示方式（不同的Basis）。
时域信号

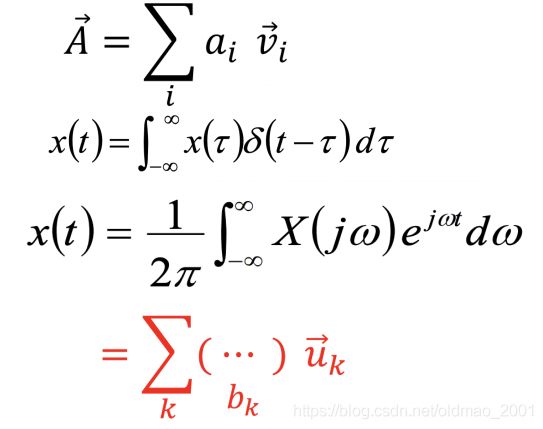
频域信号

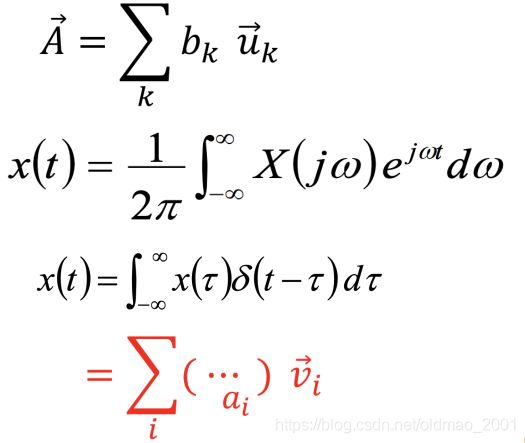
变化要借助的是傅里叶变化

Spectral Graph Theory

notation：
Graph: G=(V,E), N=|V|(节点数量)
邻接矩阵：w是相连节点的边的权重

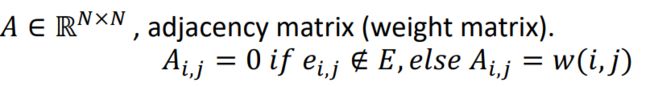
度矩阵，是一个对角（且对称）矩阵，记录了节点的邻居：

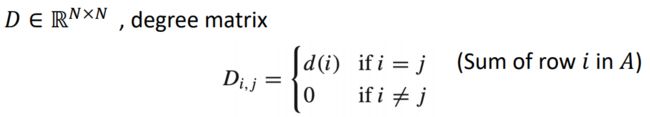
向量f(V)，代表节点上的信号

例子：

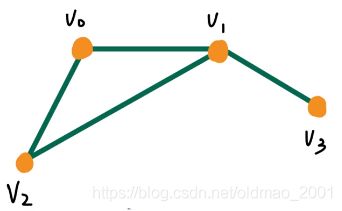
加入信号表示为，信号可以表示为节点的属性，例如路网图，那么节点表示某地区的气温之类的信息（这里信号表示可以是常量也可以是向量）：

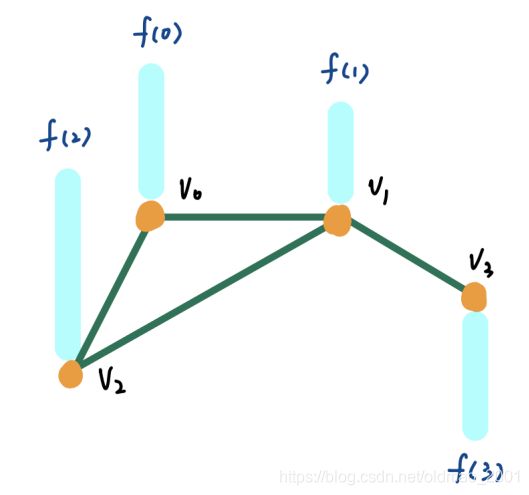
图的laplacian矩阵L，其定义是：度矩阵-邻接矩阵，度矩阵和邻接矩阵都是对称的，所以L也是对称的，而且还是半正定的矩阵。因此可以分解为：$L=U\wedge U^T$，其中U是特征向量，$\wedge$是特征值

接上面的例子。并给出具体的向量表示：

写出邻接矩阵A和度矩阵D：

然后算出拉普拉斯矩阵D-A

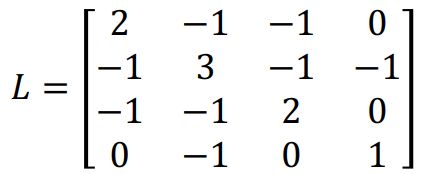
然后计算L的特征值和特征向量
由于L是半正定矩阵，所以算出来的特征值都是大于等于0的

算出来的特征向量为：

红字标出来是每个特征值对应的特征向量（一个值对一列）。
每个列可以表示到图上：

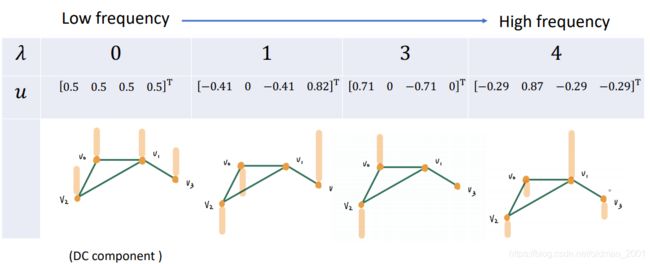
Discrete time Fourier basis

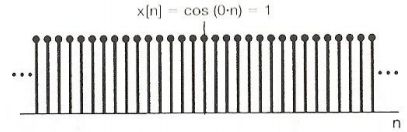
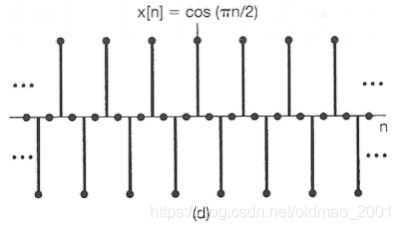
从上到下，看到频率越大，相邻两点之间的信号变化越大，最下面的相邻信号是相反的。这个概念很重要，可以用来解决GNN中的节点信号推断的问题。
把拉普拉斯矩阵作为一个运算符，对图上的信号f进行运算：$Lf$。
$$Lf=(D-A)f=Df-Af$$
用上面的图做例子，算一下$Lf$

以计算$Lf$中的a为例：a等于D中的第一行乘以f减去A的第一行乘以f。


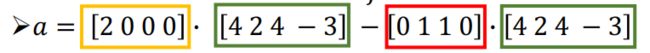
对照下图来看计算这个a的过程是什么意思：
第一个蓝色圈圈2表示$v_0$的邻居个数
第二个蓝色圈圈4表示$v_0$的信号
第三、四个蓝色圈圈分别表示$v_0$的邻居的信号

当然表示两个信号的差异的方法是取平方，因此数学上表示为：

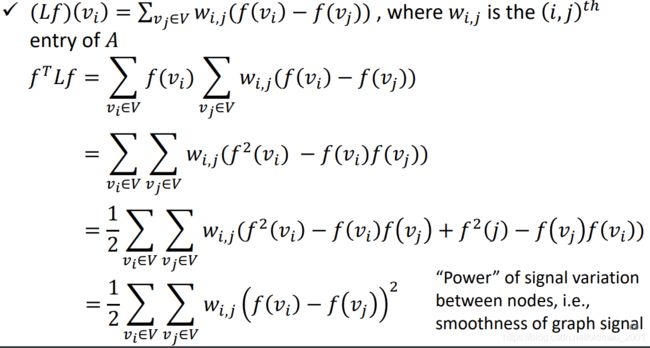
上面的$(f(v_i)-f(v_j){)}^2$表示节点i和j之间的信号能量差。能量差越小，信号越smooth，就像上面信号图一样，能量差为0就是第一个图片了。
因此：$f^{T}Lf$可以用来表示能量差。代入具体值：
$$u_i^{T}L{u}_i=u_i^T{\lambda }_i{u}_i=\lambda u_i^T{u}_i={\lambda }_i$$
这样变化以后，就得到：特征值就可以代表当前节点和相邻节点的能量差，会看上面的图：

节点0的特征值为0，所以它和他的相邻节点的能量差为0，能量差越小，越平滑，所以看到它和相邻节点的能量（频率）都同向，同大小。
看一个极端的例子，假设我们的图是一个直线，共有20个节点：

可以看到$\lambda$变大后的频率变化：

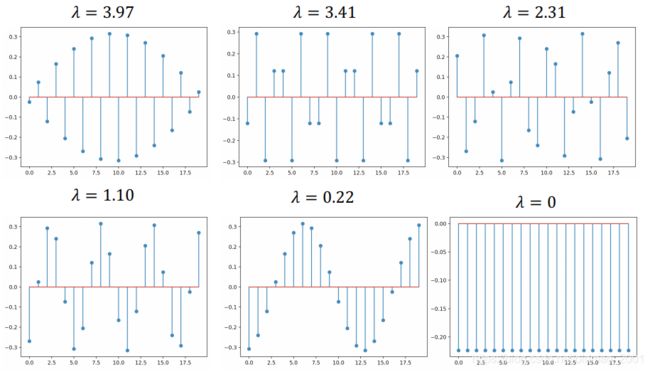
以上内容就是要为接下来的GNN中的傅里叶变化做的铺垫。
先来看普通的信号的傅里叶变化

推广到图信号的傅里叶变化：
Graph Fourier Transform of signal x:$\hat{x}=U^{T}x$
x相当于铺垫中的f；
U相当于铺垫中的特征值堆叠起来的向量


当然把上面的箭头反向回去也是可以的。（上面的箭头方向是把time domain信号转回frequency domain信号，如果反过来就是frequency domain信号转time domain信号）下面看反过来怎么搞，也是先看普通信号，再推广到图信号
下面是普通信号：求$t=t_0$时刻的时域信号强度：注意框框的颜色是对应的，最上面是表达式。

下面是图信号的frequency domain信号转time domain信号：
下面是U

下面相当于$\hat{x}$

注意上面的颜色，合成计算：

下面找出在GNN 上做filter的方式：

Filtering

先看普通的滤波怎么做：
modifying the amplitude/ phase of the different frequency components in a signal, including eliminating some frequency components entirely.
– frequency shaping, frequency selective

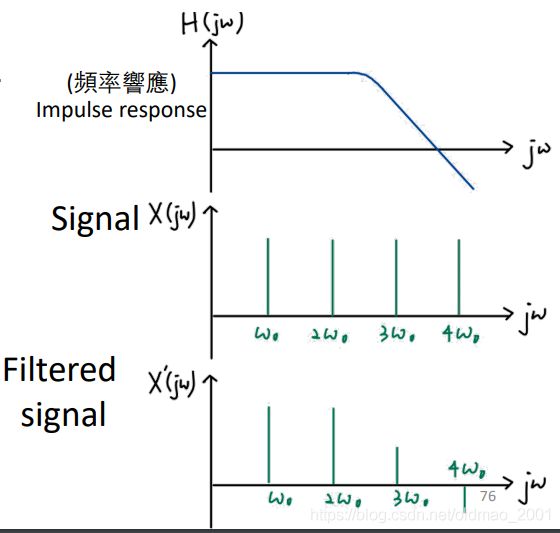
再看GNN的滤波：
Filtering: Convolution in time domain is multiplication in frequency domain.在时域的卷积相当于频域中做乘法。

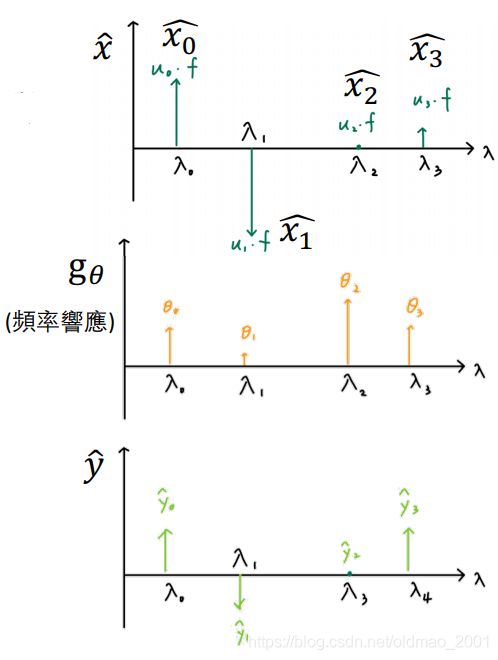
把之前的内容代入上面的公式：



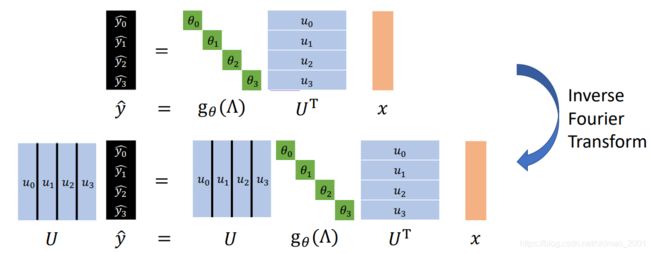
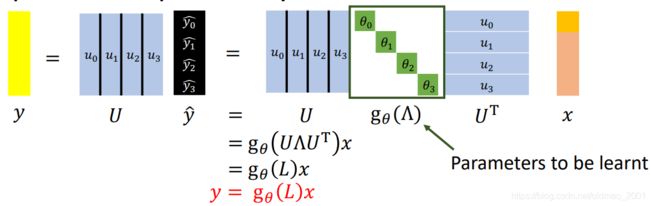
这个问题有点麻烦，在CNN中，无论输入多大，我都可以用3×3或者5×5大小的卷积核来进行卷积，这里推理出来的卷积操作需要的$g_{\theta }$的维度和输入的图的维度有关，这样在复杂度上不说了，就是失去了灵活性，没有了参数共享的优势。不同类型的图需要的卷积核不一样大。
第二个问题，由于$g_{\theta }$可以为任意函数，如果取$g_{\theta }(L)=L$，可以看到下面第一行的最后一个为0，因为当距离为1的时候，$v_0$和$v_3$不相邻


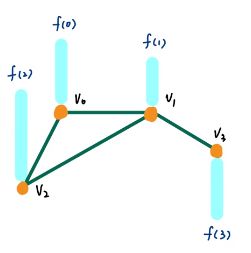
如果取$g_{\theta }(L)=L^2$，可以看到下面第一行的最后一个不为0，因为当距离为2的时候，$v_0$和所有节点相邻

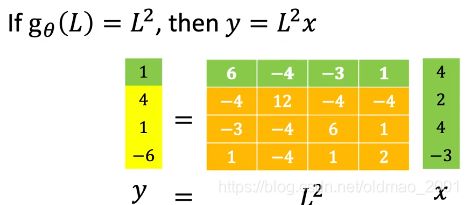
因此可以推理我们用$g_{\theta }(L)=L^N$，那么有N个节点的图在做filter运算的时候每个节点都会受到来自其他所有节点的影响。这个有点类似CNN中的感受野的概念，CNN中filter越大，看到（覆盖）的图像面积越大。
所以，第二个问题就是Not localize
两个问题的解决方案ChebNet。

ChebNet.17年

https://arxiv.org/pdf/1606.09375.pdf
思想是把$g_{\theta }(L)$定为拉普拉斯的K项多项式，使得卷积操作是K-localized（解决问题2）

而且使得要学习的参数从O(N)变成了O(K)（解决问题1）
用了这个之后，卷积操作的时间复杂度变比较高：$O(N^2)$（问题三出来了）


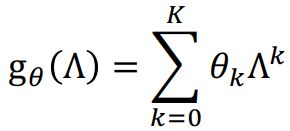
解决问题三：
Use a polynomial function that can be computed recursively from L
Chebyshev polynomial

把x替换为$\tilde{\Lambda }$

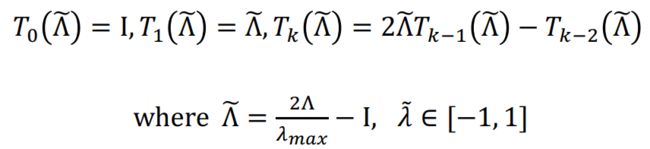
那么拉普拉斯多项式就变成：

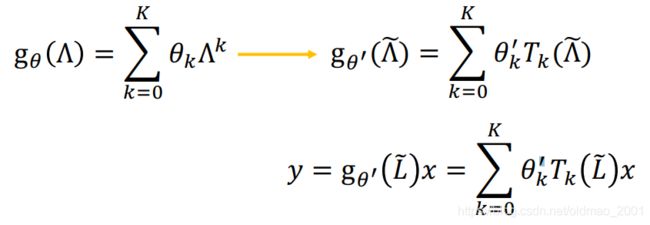
整理要filter的信号y：


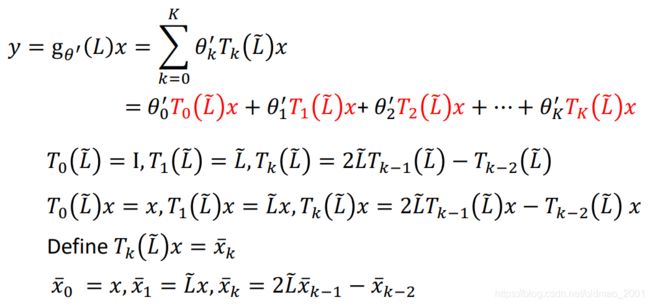
上面是递归的操作。

GCN

Graph Convolutional Networks 就是用上面的公式，设置k=1

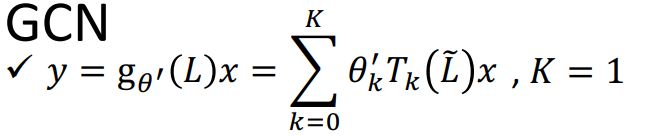
展开：

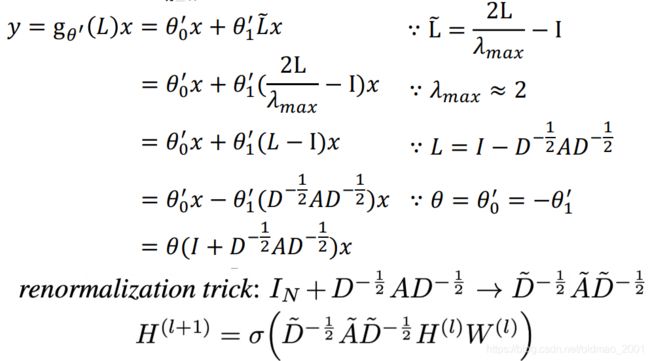
最后形式：

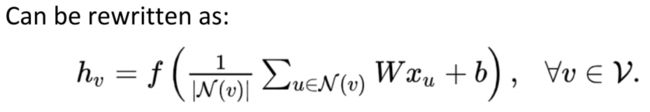
大概意思是邻居乘以w取平均，然后加上bias，经过激活函数得结果。

Graph Generation

VAE-based model: Generate a whole graph in one step
GAN-based model: Generate a whole graph in one step
Auto-regressive-based model: Generate a node or an edge in one step

VAE-based mode

https://arxiv.org/pdf/1802.03480.pdf

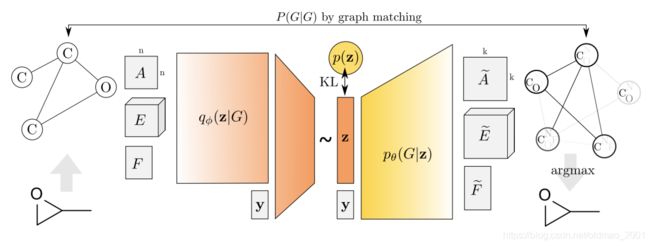
GAN-based model

https://arxiv.org/pdf/1901.00596.pdf

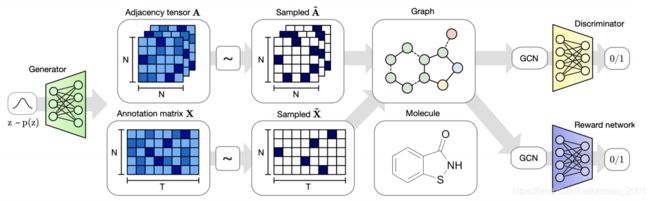
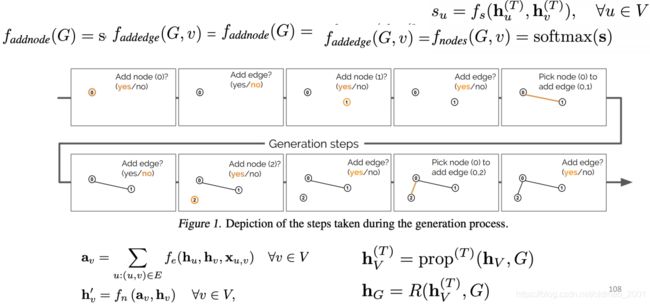
AR-based model

https://arxiv.org/pdf/1803.03324.pdf
思想一步步的来，先问是否要生成节点，然后是否要生成边，然后重复这个动作。

GNN for NLP（略）

Semantic Roles Labeling
Event Detection
Document Time Stamping
Name Entity Recognition
Relation Extraction
Knowledge Graph

Summary and Take Home Notes

GAT and GCN are the most popular GNNs
Although GCN is mathematically driven, we tend to ignore its math
GNN (or GCN) suffers from information lose while getting deeper
Many deep learning models can be slightly modified and designed to fit graph data, such as Deep Graph InfoMax, Graph Transformer, GraphBert（效果不好）.
Theoretical analysis must be dealt with in the future
GNN can be applied to a variety of tasks

Online Resources

Functions of Matrices: Theory and Computation
Signal and System by Prof. Lee:
http://speech.ee.ntu.edu.tw/courses.html
Machine Learning by Prof. Hung-yi Lee
http://speech.ee.ntu.edu.tw/~tlkagk/courses.html
Vertex-Frequency Analysis of Graph Signals