深度之眼Paper带读笔记GNN.07.GraphSAGE

前言

本课程来自深度之眼，部分截图来自课程视频。
文章标题：Inductive Representation learning on Large Graphs
大规模网络的归纳式学习（GraphSAGE）
William L. Hamilton
Rex Ying
Jure Leskovec
单位：斯坦福
发表会议及时间：NIPS 2017

公式输入请参考：在线Latex公式
inductive概念就是说它是对没有见过的图，或者说没有见过的点是有这种学习能力的，所以这篇论文的主要亮点就是 inductive。
因为GAT那边算法其实是出现在GraphSAGE之后的，在GAT那篇论文当中的实验部分其实已经看到了，它是将GraphSAGE作为一个baseline去做对比的。
GraphSAGE中，sa其实是sample的意思，也就是说它会在一个点的周围去sample一个固定size neighbors来去做一个消息的聚合，然后 ge表示的是aggregate，也就是他们的聚合的方式。
这篇论文的三者是来自于斯坦福大学的Jure（战斗民族口音那位），我们之前讲过的 Node2Vec那篇论文也是来自Jure，然后第一作者是 William L.Hamilton，他在图神经网络、NLP领域都是一个比较知名的学者。

论文结构

0. 摘要：介绍图的广泛应用，主要引出本文的motivation是做图的归纳式学习，通过学习一组函数对节点的邻居采样然后汇聚得到向量式表达。（这篇论文最重要的一个 contribution: Inductive learning）
1. Introduction：介绍图的广泛应用，总结之前的工作主要是基于静态图的算法，GraphSAGE处理新点甚至是新图，总结了DeepWalk、Node2Vec、GCN等算法，提出本文算法主要是训练aggregate函数。
2. Related work：介绍之前的算法，基于随机游走、矩阵分解、kernel、图卷积的算法。
3. GraphSAGE模型：前向传播算法，模型参数介绍，aggregator模型结构。
4. Experiments：实验设置，数据集选择，直推式学习实验，参数分析，不同aggregate函数对模型的影响分析。
5. Theoretical Analysis&Conclusion：总结提出的GraphSAGE模型具有归纳式学习的能力，邻居汇聚时考虑不同的aggregator方式，讨论几种未来方向如subgraph embedding、邻居采样方式、多模态图。

学习目标

图中有一处笔误：pooling

导读

研究背景

两个目标：

1. 希望将节点映射到低维向量上（Encoder maps each node to a low dimensional vector.）
   $$ENC(v)=z_v$$
2. 相似度目标，就是在低维向量空间中，也就是 $z_v$这个低维的空间上，它要保持在原来的网络之间的结构，比如$u,v$这两个点，在原来不做任何变换之前，他们在图结构中的相似度比较高，那么在映射之后的它们这两个向量之间的相似度（点乘的结果值）相对也较大。
   $$simlarity(u,v)\approx z_v{z}_u$$

消息的聚合：
借鉴的是CNN的filter操作

notation

· Assume we have a graph $G$:
·$V$ is the vertex set. 节点集合
·$A$ is the adjacency matrix(assume binary). 图的邻接矩阵（输入）
· $X\in R^{m\times |V|}$ is a matrix of node features. 点特征矩阵（输入）可以是下面的东西：
· Categorical attributes, text, image data. E.g., profile information in a social network.
· Node degrees, clustering coefficients, etc.（聚集系数是衡量这个点的周围邻居的密集度的信息，比如1个点有10个邻居，它衡量的是你和邻居之间，他们形成的网络是否密集，如果图中节点两两都认识，这种网络肯定是最密的）
· Indicator vectors(i.e., one-hot encoding of each node)
说明：我们复现用的是cora数据集，因此，它的特征$X$已经给定了，但是大家如果去做一些比较新型的实验，有时 feature都要靠你自己去抽取（特征工程）。

图卷积

. Nodes have embeddings at each layer. 每一层的维度可以不一样
· Model can be arbitrary depth.理论上可以做任意层的深度，但是硬件限制，后面会有一个算法可以做到10-20层，借鉴的是RNN的思想。
·“layer-0” embedding of node $u$ is its input feature,i.e.$x_u$.

这里卷积后消息的聚合可以有很多种方式，常用的就是做平均、求最大等，上图中只对邻居信息做了聚合，实际上我们还可以在上面右图中虚线箭头的地方concat上节点本身的embedding，在进行聚合操作（在下图中的橙色方框表示就是节点本身。）。
Basic approach:Average neighbor information and apply a neural network.

上面的公式中可以看到对邻居和对自身处理使用了不同的参数(在两个是要训练反向传播更新的东西)：$W_k,B_k$。其中k表示不同的层。
最后经过$K$层的聚合（图卷积）得到我们想要的结果：
$$z_v=h_v^K$$
After K-layers of neighborhood aggregation, we get output embeddings for each node.
We can feed these embeddings into any loss function and run stochastic gradient descent to train the aggregation parameters.

GCN/GAT/GraphSAGE通用流程

下面总结一下GCN/GAT/GraphSAGE的通用的流程。
第一个：要定义一个邻居的汇聚的方式，即如何将节点邻居的信息去汇聚为一个vector，然后和节点本身的vector去拼接起来，或者说怎么用什么样的方式将邻居的特征去表示成你要用的特征。
第二步：定义一个损失函数值，这样才能用反向传播算法去更新我们设计的这些参数，比如说刚才我们看到的$W_k,B_k$。

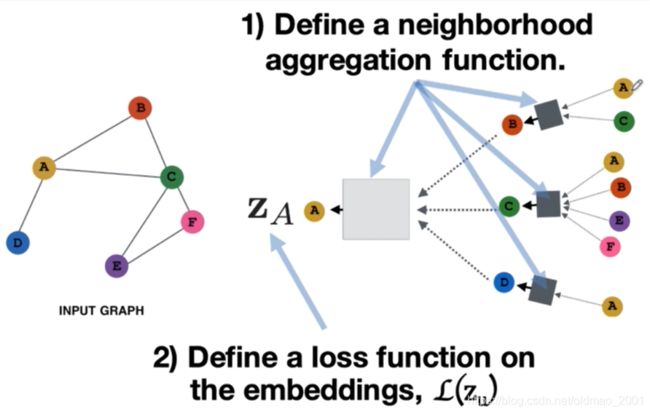
第三步是节点的选取（batch的算法），对于每一个点来说都是一个计算图，比如说对于黄色这个点，它的一跳邻居其实是bcd这三个点（分别是蓝色、绿色还有红色），同样的对于蓝色的一跳邻居就是a只有黄色这一个点。上篇GAT论文中是针对所有节点进行训练的（有的同学反应说GAT跑起来报内存不足，估计就这个原因。），而GraphSAGE是针对某个batch进行训练的。

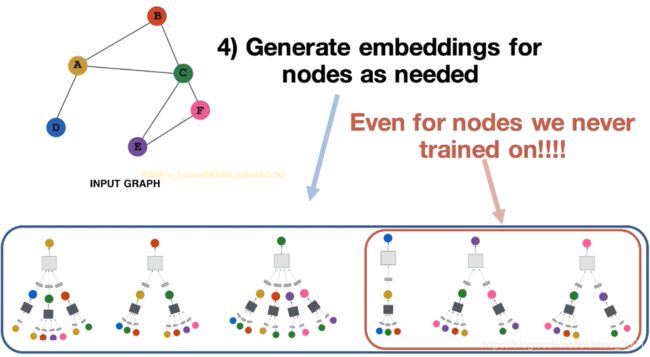
第4步：对于所有的点，模型通过学习出来的参数$W_k,B_k$，将节点的邻居特征去聚合到节点本身，然后包括一些维度的变化，这些都是模型要处理的。最开始学习的Node2Vec模型，只能学习到几个function然后吃节点吐对应的embedding。而GAT、GraphSAGE则拥有inductive的能力，例如下图中右下角有个红框中的图汇聚方式是模型没有见过的，但是模型通过学习得到里面的灰色和深灰色小方块（就是function及参数），可以将邻居进行汇聚操作，得到节点的embedding表示。

研究意义

GraphSAGE（SAmple and aggreGatE）意义
·图卷积神经网络最常用的几个模型之一（GCN，GAT，GraphSAGE）
·归纳式学习（inductive learning）
·不同于之前的学习node embedding，提出学习aggregators等函数的方式
·探讨了多种的aggregator方式（mean，pooling，LSTM）
·图表征学习的经典baseline

泛读

摘要核心

1.本文提出了一种归纳式学习模型，可以得到新点/新图的表征。
Here we present GraphSAGE, a general inductive framework that leverages node feature information (e.g., text attributes) to efficiently generate node embeddings for previously unseen data.
2.GraphSAGE模型通过学习一组函数来得到点的表征。之前的随机游走方式则是先随机初始化点的表征，然后通过模型的训练更新点的表征来获取点的表征，这样无法进行归纳式学习。
Instead of training individual embeddings for each node, we learn a function that generates embeddings by sampling and aggregating features from a node’s local neighborhood.
3.采样并汇聚点的邻居特征与节点的特征拼接得到点的特征。
4.GraphSAGE算法在直推式和归纳式学习均达到最优效果。

论文结构

1. Introduction
2. Related work
3. Proposed method: GraphSAGE
   3.1Embedding generation(i.e, forward propagation) algorithm
   3.2 Learning the parameters of GraphSAGE
   3.3 Aggregator Architectures
4. Experiments
   4.1Inductive learning on evolving graphs: Citation and Reddit data
   4.2 Generalizing across graphs:Protein-protein interactions
   4.3Runtime and parameter sensitivity
   4.4 Summary comparison between thedifferent aggregator architectures
5. Theoretical analysis
6. Conclusion

论文精读

论文算法模型总览

GNN结构回顾

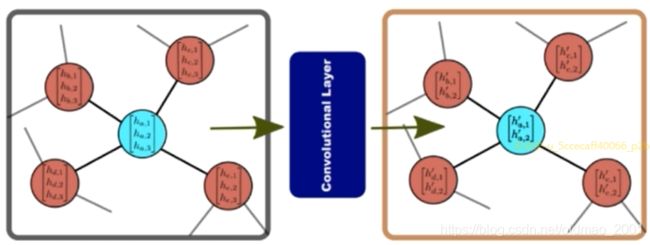
Building Block of GCNs
For each node in the graph, a convolutional operator consists of two main steps:
Aggregation of neighbouring node features.
Applying a nonlinear function to generate the output features.
Complete GCN consists of multiple convolutional layers.
GAT里面有讲，这里不重复了

GraphSAGE结构

第一步：sample一些neighbor的node，比如说以红色点为中心，可以看到是一个两层的图神经网络，第一层中k=1，红色的点其实有5个邻居节点（看下左边小的虚线圆圈里面）除了三个橙色的点，还有两个白色的点，但是模型用到了sample的概念，GAT/GCN则是对于当前节点的所有的邻居节点都考虑了，但是GraphSAGE的一个特点就是只是去sample一定固定size大小的节点，下图中采样大小是3。
他为什么要这么做？
这和GraphSAGE的aggregate方式是有关。比如GraphSAGE会用到一个LSTM的aggregate方式，而LSTM需要输入长度是等长的，在NLP中如果是不等长的时候，是要进行padding的。

第二步：从邻居进行 aggregate。GraphSAGE的aggregate方式有：mean、pooling。下图中有蓝色和绿色的箭头，蓝色代表第一层的参数（$W_1$），绿色代表第二层的参数（$W_2$）。
第三步：利用第二步汇聚得到信息对节点进行预测，下图中可以明显看到节点有label，得到邻居汇聚信息后，我们可以先做softmax，然后再和label做交叉熵。这样就可以计算Loss，然后反向传播。

下面我们就来看一下模型的具体的流程（这里和前面讲通用流程的内容有些重复）
下图中A是我们要学习embedding表示节点，其有三个邻居分别是：BCD。因此在右边可以看到展开后变成从BCD进行消息传递/汇聚。

上图中的公式$h_v^k$的h表示A这个点的embedding表示，v代表A这个节点，k代表第几层
AGG就是指aggregate操作，当然这里有很多种选择
u代表v的邻居节点：$\forall u\in N(v)$
蓝色矩形就是表示对v这个节点的所有邻居进行汇聚操作
$A_k$相当于前文讲的$W_k$，是要学习的参数
$B_k$对应自身节点的参数
然后[]表示将两个信息进行concat
最外面的$\sigma$表示非线性变换

模型细节一：算法说明

这里输入就是图$G=(V,E)$，每个顶点都有特征$\{x_v,\forall v\in V\}$
模型有K层，每层的参数记为：$W^k,\forall k\in \{1,...,K\}$
然后邻居表示为0/1的形式：$v\to 2^v$
第一步：就是要获得第0层的embedding表示$h_v^0$，这个embedding直接由邻居节点的特征进行汇聚操作得来
从第二步开始进行K层的GNN卷积操作。
第四步表示从第k-1层的v的邻居进行聚合
第五步表示从第k-1层的本身和上一步的结果进行concat，然后做非线性操作
第七步进行归一化操作

模型细节二：直推式+归纳式学习

原文对应3.2节
无监督（直推式）：
Loss：附近的节点具有相似的embedding表示，不同节点的embedding表示不同（negative sampling），原文给出的损失函数和Node2Vec等随机游走方式的损失函数思想是一样的，都是正样本的表征要越近越好，负样本的表征要越远越好，而且这里也是用到了负采样技术，其中的Q表示负采样的个数。
$$J_g(z_u)=-\log (\sigma (z_u^{\top }{z}_v))-Q\cdot E_{v_n\sim P_n(v)}\log (\sigma (-z_u^{\top }{z}_v))$$
有监督（归纳式）：
cross-entropy loss

再次加一点总结：
直推式学习是把一个图分训练集、验证集和测试集，然后在一张图上进行预测；归纳式学习是在很多张图上进行训练，然后在新的图上做预测。

模型细节三：聚合方式

原文3.3小节
与传统机器机器学习中的N维切片不同，传统的句子、图片等数据进行多层卷积的时候都是有先后顺序的，而在图中的节点与节点之间是没有这样的顺序结构的（假设1个点有10个邻居，这10个邻居是没有顺序这种信息的），因此图选择聚合操作是针对无序集合的，因此是一种对称的操作。例如：使用mean作为聚合方式，10个节点的embedding进行平均后，打乱节点的顺序，它们的平均值都是一样的，所以mean就是天然的符合这种性质的函数。

$$h_v^k=\sigma ([W_k\cdot AGG(\{h_u^{k-1},\forall u\in N(v)\}),B_k{h}_v^{k-1})$$
这里AGG可以是如下几种形式：
1.Mean
$$AGG=\sum _{u\in N(v)}\frac{h_u^{k-1}}{|N(v)|}$$
上式中对于v的所有邻居节点求和，将所有邻居节点的embedding求和后除以邻居节点的数量做平均（进行归一化）,整个模型变成：
$$h_v^k=\sigma \left(W_k\sum _{u\in N(v)}\frac{h_u^{k-1}}{|N(v)|}+B_k{h}_v^{k-1}\right)$$
原文的公式是（原文貌似少一个反括号，不知道是不是正式版本）：
$$h_v^k=\sigma \left(W\cdot \text{MEAN}(\{h_v^{k-1}\}\cup \{h_u^{k-1},\forall u\in N(v)\})\right)$$
这里原文也提到，要加入本身节点进行计算，但有不直接参与邻居的平均值计算，而是另外处理，就相当于自己本身对自己的影响和邻居带来的影响不一样，同时也契合resnet的思想。
2.Pool
先对节点的邻居节点进行一个投影变化（乘以一个Q矩阵，该矩阵可学习，做完后维度可以变化），然后再进行对称向量化（symmetric vector）操作（通常是element-wise的 mean/max操作，就是下面的$\gamma$）
$$AGG=\gamma (\{{\text{Qh}}_u^{k-1},\forall u\in N(v)\})$$
原文给出的公式是：
$$AG{G}_k^{pool}=max(\{\sigma (W_{pool}{h}_{u_i}^k+b),\forall u_i\in N(v)\})$$
原文的描述就是把每个邻居节点都单独丢进一个任意深度的感知机perceptron（当然本文只用了一层），然后做max pooling
3.LSTM
由于LSTM本来是处理序列的，但是节点本身又是无序的，因此这里用了一个随机乱序输入trick，可以将邻居节点（随机sample，公式中用$\pi$表示）的embedding表示作为一个序列丢进LSTM中得到当前节点的embedding：
$$AGG=\text{LSTM}(\{{\text{h}}_u^{k-1},\forall u\in \pi N(v)\})$$

模型细节四：Batch训练

在附录A中还有一个算法2：

这里面对输入做了限制，不是针对所有节点，而是对一个batch的节点$\forall v\in B$
从第二步到第七步是将batch中K层的邻居都加进来
从第九步开始进行K层的GNN卷积操作
第十步是开始对所有收集到的batch的邻居节点进行操作
第k层的节点更新k次，最外层的节点只会更新一次。

模型细节五：理论分析

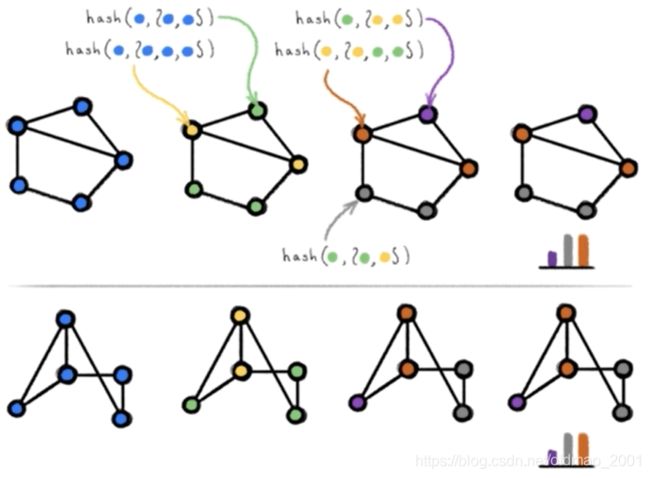
WL-test: 就是要判断两个图是否同构，这个问题比较难计算，甚至超越NP问题，WL-test在大多数情况可以解决判断同构问题，具体可以参考：
https://zhuanlan.zhihu.com/p/90645716
Hard to compute
Right algorithms in most cases
通过聚合节点邻居标签信息，然后通过hash函数得到节点新的信息，不断重复，直到每个节点的标签信息稳定不变。例如上图中最后每个点的信息分布一致，所以认为两个图同构。
下面看具体例子：
给定如下两个图$G$和$G^{\prime }$：

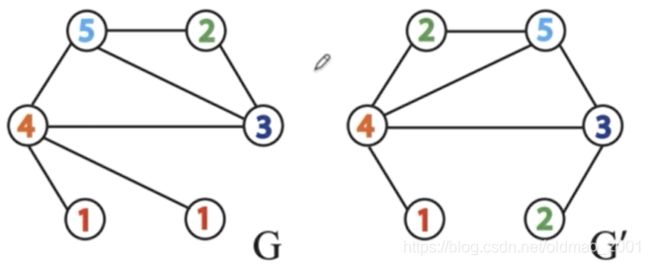
第一次聚合邻居信息（邻居信息默认采用升序）：

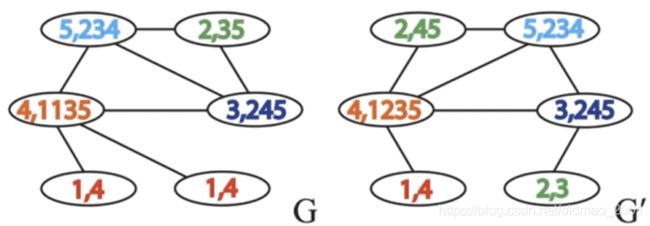
为了能够生成一个—一对应的字典，我们将每个节点的字符串hash处理后得到节点的新ID
将哈希处理过的ID重新赋值给相应的结点，以完成第一次迭代。节点哈希表如下图所示：

迭代的结果：G=6、6、8、10、11、13，G’=6，7，9，10，12，13。
如果两个图同构的话，在迭代过程中G和G’将会相同。

WL-test:GNN的性能上界
GNN与WL-test的联系：
用单层感知机近似HASH函数，GraphSAGE用加权平均替代邻居信息拼接，加权平均过程中是会丢失掉一些信息的，而不像信息拼接是保留了所有的信息。用单层感知机也是近似hash函数也是会丢失信息。

参考阅读：
K.Xu et al.How powerful are graph neural networks？（2019）.Proc.ICLR.
在原文的第五节理论分析中，还给出了一个定义，其中涉及到了聚集系数的概念，其公式如下：
$$\begin{gathered} C_i=\frac{2|\{e_{jk}:v_j,v_k\in N_i,e_{jk}\in E\}|}{k_i(k_i-1)} \\ =\frac{|\{e_{jk}:v_j,v_k\in N_i,e_{jk}\in E\}|}{\frac{k_i(k_i-1)}{2}} \end{gathered}$$
其中分母$\frac{k_i(k_i-1)}{2}$当图中k个邻居节点是完全图的时候的图中边的数量（详见数据结构图的性质），分母则表示当前图中边的数量，聚集系数表示当前图k个邻居与其完全图的接近程度，越接近，那么当前图越稠密，反之越稀疏。
例如下图中蓝色节点有三个邻居，那么蓝色节点的聚集系数分别是1、1/3、0。

原文的第五节实际上是说可以用GraphSAGE来预测图的节点的聚集系数，而且精度非常高（误差小于一个任意小的数$ϵ$），原文描述如下：

这个定理有一些限制，第一个是对于两个输入的特征要大于C，也就是不等于0，也就是不能相同的意思，这里特征不能相同意味着两个输入节点拓扑不能相同，例如不能都有相同的邻居，这个限制有点高，第二个是要对数据进行4次图卷积操作，这个也是理论上的东西，实际做图卷积大多是2-3层。
具体证明见原文附录E。

实验设置及结果分析

见原文第四节

数据集介绍：

Citation data: undirected citation graph, 6 labels, 302,424 nodes, X=node degree + sentence embedding
Reddit data: undirected post graph, 50 labels, 232,965 nodes, X=[post title embedding; post’s comments; post’s score; the number of comments]
PPI data: undirected post graph, 121 labels, (20+2+2) ×2373 nodes, X=[gene sets.…]

来看一下这篇论文用到的数据集，第一个数据集是用了citation的一个网络，这是一个无向图，然后每个点其实表示的是一篇论文，该数据集是一个citation关系的网络。也就是说如果两个点之间有条边，它表示这两个点之间，即这两个论文之间有一个引用关系，这是一个6分类的问题，点数是大概有30万个点，它的输入X的特征是多个属性拼接起来的：第一个是节点的度，第二个是文章的embedding，比如可以算一下这篇论文的title的embedding，以得到一个关于这篇论文的内容的特征。sentence embedding的具体的方式是将某篇论文丢进word2vec（用的是GenSim，300维）进行pretrain。
第二个网络是Reddit ，也是一个无向图，然后它是一个post graph，post就是类似论坛中的发帖的意思，每一个节点相当于一个post，每个评论都有一个类别，例如科幻、IT、商品推荐等等，这里节点的边是当同一个用户都对两个post进行了打分或者浏览，那么就为两个post建立一条边。这个图大约有23万个点，每个点的特征X是拼接的上面的分号代表concat查找，前面两个是embedding（用GloVe，300维），后面两个是实数。number of comments表示这个发帖收到的回复数量。因此这个特征X是需要进行一些预处理的，不是直接给的。
这两个数据集都是用的直推式的学习
PPI这个在GAT里面有介绍过，是用来做归纳式学习的。不展开。

然后它的 label选的输入的特征x它都是通过一些自己的计算，它也是通过 post开头，它做了一个引白顶，相当于也是一个sentence引白顶，还有你 post上面有好多 comment，它也做了一个引白顶，这些分号表示这些vector都是拼接的，然后后边还有两个实数的特征，那一个是 post它有一个打分也就是一个score，还有一个就是说你这篇pose它收到多少个comments，这样的话它这有一个数量，所以是两个 in，biting the lecture去做一个拼接，然后再和两个实数的拼接得到 x所以它都是有一个preprocessing的过程。

这个特征x不是特意给出的，都是需要自己去计算的。

节点分类任务

上表中针对三个数据集分别有两列，一列是无监督、一列是有监督。
第三行是DeepWalk：直接使用网络的拓扑结构去做预测
第四行是DeepWalk+feature：用网络的拓扑结构得到节点的embedding，然后和特征X做concat，然后经过FC层，然后进行softmax分类预测。
明显看到第四行效果要比第三行好，因为我们为模型提供的信息更加多了。

然后后面四行是对GraphSAGE四种不同的汇聚方式进行了比较，可以看到在不同的数据集上不同的汇聚方式取得效果也各有优点。

运行效率以及参数分析

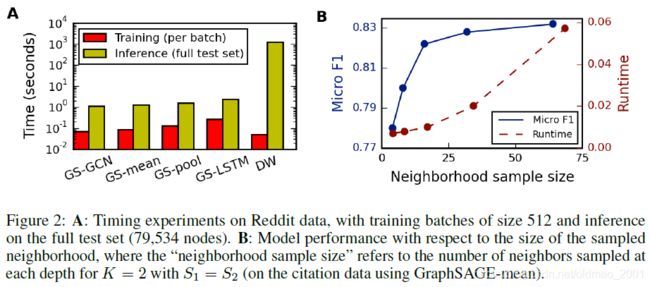
A这张图它表示的是在 Reddit 的数据集上，training（红色）的实验中，batchsize设为512，也就是每一次训练512个点，inference（黄绿色）则在整个测试集中进行（共计79,534个点）因此可以看到inference的时间柱要比training的时间柱要长。
注意：同样的点的数量的时候肯定是 inference要快，因为不用去更新参数，只做前向传播，不用做后向传播。
DW代表DeepWalk，可以看到DW需要对图进行游走进行采样，生成序列，这个步骤是比较花时间。另外DW对于新点的计算还要额外进行GD，原文4.3节：However, the need to sample new random walks and run new rounds of SGD to embed unseen nodes makes DeepWalk 100-500× slower at test time.
B这个图主要演示GraphSAGE做sample的时候sample不同数量的邻居会有什么不一样的效果，GAT就没有这个东西，因为GAT是对所有邻居进行汇聚的，不做sample。从图中可以看到，sample的数量越大，运行所需要的时间也就越多，但是同时微观F1值越大，这个时候图中表达的是，当我们取某一个合理的sample size，微观F1会有比较大的提升。
对于GNN的层数效率的分析：
however, increasing $K$ beyond 2 gave marginal returns in performance (0-5%) while increasing the runtime by a prohibitively large factor of 10-100×, depending on the neighborhood sample size.
原文的4.4节对不同的聚合方式（三种加GCN）进行了统计上的显著性分析实验，具体结论如下：
1、本文的三种聚合方式要比GCN聚合要好
We see that LSTM-, pool- and mean-based aggregators all provide statistically significant gains over
the GCN-based approach (T = 1:0, p = 0:02 for all three).
2、LSTM, pool要比mean方式好
However, the gains of the LSTM and pool approaches over the mean-based aggregator are more marginal (T = 1:5, p = 0:03, comparing LSTM to mean; T = 4:5, p = 0:10, comparing pool to mean).
3、LSTM和 pool差不多（无显著差异），但是pool速度比较快。
There is no significant difference between the LSTM and pool approaches (T = 10:0, p = 0:46). However, GraphSAGE-LSTM is significantly slower than GraphSAGE-pool (by a factor of ≈2×), perhaps giving the pooling-based aggregator a slight edge overall.

论文总结

关键点

模型结构
邻居sample以及LSTM顺序
Batch训练方式

创新点

归纳式学习（重点）
多种aggregators的探讨
理论分析

启发点

归纳式学习的方式，演化图以及完全的新图
多种aggregators函数的讨论
Batch训练方式，sample邻居，性能高效
GCN、GAT、GraphSAGE都是非常重要的模型，也是经典baselines
与GNN常用框架之间的联系

代码复现

原文项目：https://github.com/williamleif/graphsage-simple/
python 3.7.6
torch 1.3.1
numpy 1.18.1
jupyter notebook/PyCharm
数据集：Cora

model.py

import torch
import torch.nn as nn
from torch.nn import init
from torch.autograd import Variable

import numpy as np
import time
import random
from sklearn.metrics import f1_score
from collections import defaultdict

from graphsage.encoders import Encoder
from graphsage.aggregators import MeanAggregator

"""
Simple supervised GraphSAGE model as well as examples running the model
on the Cora and Pubmed datasets.
"""

class SupervisedGraphSage(nn.Module):

    def __init__(self, num_classes, enc):
        super(SupervisedGraphSage, self).__init__()
        self.enc = enc#这里面赋值为enc2（经过两层GNN的结果）
        self.xent = nn.CrossEntropyLoss()
        
        #全连接参数矩阵，映射到labels num_classes维度做分类，维度是7*128
        self.weight = nn.Parameter(torch.FloatTensor(num_classes, enc.embed_dim))
        init.xavier_uniform(self.weight)

    def forward(self, nodes):
        #embeds实际是我们两层GNN后的输出nodes embedding，enc就是enc2
        embeds = self.enc(nodes)
        #最后将nodes*hidden size 映射到nodes*num_classes（这里是7分类）之后做softmax计算cross entropy
        scores = self.weight.mm(embeds)
        return scores.t()

    def loss(self, nodes, labels):
        scores = self.forward(nodes)
        return self.xent(scores, labels.squeeze())

def load_cora():
    num_nodes = 2708#节点数量
    num_feats = 1433#特征数量
    feat_data = np.zeros((num_nodes, num_feats))#初始化特征矩阵:2708*1433全零矩阵
    labels = np.empty((num_nodes,1), dtype=np.int64)#初始化ground truth标签：1433*1
    #重新按顺序设置点的id
    node_map = {}
    #重新按顺序设置label的id
    label_map = {}
    
    #读节点特征
    #cora.content第一列是node id，中间为点的特征，最后一列为label
    #with open（"cora/cora.content"）as fp：
    with open("..cora/cora.content") as fp:
        for i,line in enumerate(fp):#按行读取文件
            info = line.strip().split()#strip去掉每行前后的内容包括换行符等，然后用split按空格分开。
            #特征处于每行的[1:-1]位置，将特征全部转换成float类型，便于后面的聚合求平均
            #feat_data[i,:] = map(float, info[1:-1])，这里是原文代码，无法运行，改为下面的代码
            tmp=[]
            for ss in info[1:-1]: 
                tmp. append(float(ss))
            feat_data[i,:]=tmp#将转换后float类型的特征放到特征矩阵中
            
            #将点的id进行转换，映射从0开始。info[0]是node old id
            node_map[info[0]] = i
            #info[-1]是label，字符串，文章类型，比如‘Neural Networks'和‘Rule Learning'，转换成int来表示文章对应分类，共有7种
            if not info[-1] in label_map:
                label_map[info[-1]] = len(label_map)
            labels[i] = label_map[info[-1]]

    #读图存储成邻接表
    #例如：(a,b)(a,c)(a,d)(b,c)(b,d)
    #存储后：{a:set(b,c,d),b:set(a,c,d),c:set(a,b),d:set(a,b)}
    adj_lists = defaultdict(set)
    with open("cora/cora.cites") as fp:
        for i,line in enumerate(fp):
            #每一行是一条边
            info = line.strip().split()
            paper1 = node_map[info[0]]
            paper2 = node_map[info[1]]
            #无向图，相互添加为邻居
            adj_lists[paper1].add(paper2)
            adj_lists[paper2].add(paper1)
    return feat_data, labels, adj_lists

def run_cora():
    np.random.seed(1)#随机数设置seed（种子）
    random.seed(1)
    num_nodes = 2708#cora数据集点数
    
    #加载cora数据集，返回的东西分别是
    #feat data：特征
    #labels：标签
    #adjlists：邻接表，dict(key:node，value:neighbors set)
    feat_data, labels, adj_lists = load_cora()
    #设置输入的input features矩阵x的维度=点的数量*特征维度
    features = nn.Embedding(2708, 1433)
    #为矩阵X赋值，作为参数该矩阵不更新
    features.weight = nn.Parameter(torch.FloatTensor(feat_data), requires_grad=False)
    # features.cuda()

    #-----模型部分-------
    
    #一共两层GNN layer
    #第一层GNN
    #以mean的方式聚合邻居，algorithm 1 的第四行
    #输入features是从cora读出来的特征矩阵
    agg1 = MeanAggregator(features, cuda=True)
    #将自身和聚合邻居的向量拼接后送入到神经网络（可选是否只用聚合邻居的信息来表示gcn=True），algorithm 1的第五行，得到维度是2708*128
    enc1 = Encoder(features, 1433, 128, adj_lists, agg1, gcn=True, cuda=False)
    #第二层GNN
    #将第一层的GNN输出作为输入传进去
    #这里面.t()表示转置，是因为Encoder class的输出维度为embed_dim*nodes
    agg2 = MeanAggregator(lambda nodes : enc1(nodes).t(), cuda=False)
    #enc1.embed dim=128，变换后的维度还是128
    enc2 = Encoder(lambda nodes : enc1(nodes).t(), enc1.embed_dim, 128, adj_lists, agg2,
            base_model=enc1, gcn=True, cuda=False)
    #采样的邻居点的数量
    enc1.num_samples = 5
    enc2.num_samples = 5

    #7分类问题
    #enc2是经过两层GNN layer时候得到的 node embedding/features
    graphsage = SupervisedGraphSage(7, enc2)
#    graphsage.cuda()
    
    #permutation做排列组合，目的是打乱节点顺序
    rand_indices = np.random.permutation(num_nodes)
    
    #划分测试集、验证集、训练集
    test = rand_indices[:1000]
    val = rand_indices[1000:1500]
    train = list(rand_indices[1500:])

    #用SGD的优化，设置学习率
    optimizer = torch.optim.SGD(filter(lambda p : p.requires_grad, graphsage.parameters()), lr=0.7)
    #记录每个batch训练时间
    times = []
    #共训练100个patch
    for batch in range(100):
        #取前256个nodes作为一个batch
        batch_nodes = train[:256]
        #打乱训练集的顺序，使下次迭代取前256个nodes时batch随机
        random.shuffle(train)
        #记录开始时间
        start_time = time.time()
        
        optimizer.zero_grad()
        #SupervisedGraphSage里面定义的cross entropy loss
        loss = graphsage.loss(batch_nodes, 
                Variable(torch.LongTensor(labels[np.array(batch_nodes)])))
        #反向传播和更新参数
        loss.backward()
        optimizer.step()
        #记录结束时间
        end_time = time.time()
        times.append(end_time-start_time)
        #print batch, loss.data[0]
        print batch, loss.data

    #做validation
    val_output = graphsage.forward(val) 
    #计算F1，用val_output中最大值的位置与label中的实际分类位置做交叉熵
    print "Validation F1:", f1_score(labels[val], val_output.data.numpy().argmax(axis=1), average="micro")
    #计算每个batch平均计算时间
    print "Average batch time:", np.mean(times)

def load_pubmed():
    #hardcoded for simplicity...
    num_nodes = 19717
    num_feats = 500
    feat_data = np.zeros((num_nodes, num_feats))
    labels = np.empty((num_nodes, 1), dtype=np.int64)
    node_map = {}
    with open("pubmed-data/Pubmed-Diabetes.NODE.paper.tab") as fp:
        fp.readline()
        feat_map = {entry.split(":")[1]:i-1 for i,entry in enumerate(fp.readline().split("\t"))}
        for i, line in enumerate(fp):
            info = line.split("\t")
            node_map[info[0]] = i
            labels[i] = int(info[1].split("=")[1])-1
            for word_info in info[2:-1]:
                word_info = word_info.split("=")
                feat_data[i][feat_map[word_info[0]]] = float(word_info[1])
    adj_lists = defaultdict(set)
    with open("pubmed-data/Pubmed-Diabetes.DIRECTED.cites.tab") as fp:
        fp.readline()
        fp.readline()
        for line in fp:
            info = line.strip().split("\t")
            paper1 = node_map[info[1].split(":")[1]]
            paper2 = node_map[info[-1].split(":")[1]]
            adj_lists[paper1].add(paper2)
            adj_lists[paper2].add(paper1)
    return feat_data, labels, adj_lists

def run_pubmed():
    np.random.seed(1)
    random.seed(1)
    num_nodes = 19717
    feat_data, labels, adj_lists = load_pubmed()
    features = nn.Embedding(19717, 500)
    features.weight = nn.Parameter(torch.FloatTensor(feat_data), requires_grad=False)
   # features.cuda()

    agg1 = MeanAggregator(features, cuda=True)
    enc1 = Encoder(features, 500, 128, adj_lists, agg1, gcn=True, cuda=False)
    agg2 = MeanAggregator(lambda nodes : enc1(nodes).t(), cuda=False)
    enc2 = Encoder(lambda nodes : enc1(nodes).t(), enc1.embed_dim, 128, adj_lists, agg2,
            base_model=enc1, gcn=True, cuda=False)
    enc1.num_samples = 10
    enc2.num_samples = 25

    graphsage = SupervisedGraphSage(3, enc2)
#    graphsage.cuda()
    rand_indices = np.random.permutation(num_nodes)
    test = rand_indices[:1000]
    val = rand_indices[1000:1500]
    train = list(rand_indices[1500:])

    optimizer = torch.optim.SGD(filter(lambda p : p.requires_grad, graphsage.parameters()), lr=0.7)
    times = []
    for batch in range(200):
        batch_nodes = train[:1024]
        random.shuffle(train)
        start_time = time.time()
        optimizer.zero_grad()
        loss = graphsage.loss(batch_nodes, 
                Variable(torch.LongTensor(labels[np.array(batch_nodes)])))
        loss.backward()
        optimizer.step()
        end_time = time.time()
        times.append(end_time-start_time)
        print batch, loss.data[0]

    val_output = graphsage.forward(val) 
    print "Validation F1:", f1_score(labels[val], val_output.data.numpy().argmax(axis=1), average="micro")
    print "Average batch time:", np.mean(times)

if __name__ == "__main__":
    run_cora()

aggregators.py

import torch
import torch.nn as nn
from torch.autograd import Variable

import random

"""
Set of modules for aggregating embeddings of neighbors.
"""

#实现聚合类，对邻居信息进行AGGREGATE
class MeanAggregator(nn.Module):
    """
    Aggregates a node's embeddings using mean of neighbors' embeddings
    """
    def __init__(self, features, cuda=False, gcn=False): 
        """
        Initializes the aggregator for a specific graph.
        features -- function mapping LongTensor of node ids to FloatTensor of feature values.
        cuda -- whether to use GPU
        gcn --- whether to perform concatenation GraphSAGE-style, or add self-loops GCN-style是否要concat节点本身或者在计算平均值的时候要加上节点本身
        """

        super(MeanAggregator, self).__init__()

        self.features = features
        self.cuda = cuda
        self.gcn = gcn
        
    def forward(self, nodes, to_neighs, num_sample=10):
        """
        nodes --- list of nodes in a batch//batch中的点的列表
        to_neighs --- list of sets, each set is the set of neighbors for node in batch//batch中每个点对应的邻居集合
        nodes和to_neighs都是list，维度大小一样 
        num_sample --- number of neighbors to sample. No sampling if None.//采样的数量，大于则只采样num_sample个，小于则采样实际所有的邻居
        """
        # Local pointers to functions (speed hack)
        _set = set
        if not num_sample is None:
            _sample = random.sample
            #首先对每一个节点的邻居集合neigh进行遍历，判断一下已有邻居数和采样数大小，多于采样数进行抽样
            #对一个batch中的每一个节点的邻接点集合set进行sample
            #samp_neighs还是一个list
            samp_neighs = [_set(_sample(to_neigh, 
                            num_sample,
                            )) if len(to_neigh) >= num_sample else to_neigh for to_neigh in to_neighs]
        else:
            samp_neighs = to_neighs
           
        #将自己也作为自己的邻居点（类似于GCN里面的A+I的操作）
        if self.gcn:
            samp_neighs = [samp_neigh + set([nodes[i]]) for i, samp_neigh in enumerate(samp_neighs)]
        
        #*拆解列表后，转为为多个独立的元素作为参数给union，union函数进行去重合并，转换成新的list后里面每个节点只出现一次
        unique_nodes_list = list(set.union(*samp_neighs))
        #节点标号不一定都是从0开始的，创建一个字典，key为节点ID，value为节点序号（old id到new id的转换，为下面列切片做准备）
        unique_nodes = {n:i for i,n in enumerate(unique_nodes_list)}
        
        #构建缩小的邻接矩阵，即这个batch所用到的点所构成的小的邻接矩阵
        #nodes表示batch内的节点，unique_nodes表示batch内的节点用到的所有邻居节点，|unique_nodes|>|nodes|
        #1en(samp_neighs)是这个batch的大小，即nodes数量，创建一个nodes*unique_nodes大小的邻接矩阵
        mask = Variable(torch.zeros(len(samp_neighs), len(unique_nodes)))
        
        #列切片，遍历每一个邻居集合的每一个元素，并且通过unique_nodes（old id）获取到节点对应的序号
        column_indices = [unique_nodes[n] for samp_neigh in samp_neighs for n in samp_neigh]   
        
        #行切片，比如samp_neighs=[{3,5,9},(2,8},{2}],行切片为[0,0,0,1,1,2]
        row_indices = [i for i in range(len(samp_neighs)) for j in range(len(samp_neighs[i]))]
        #利用切片创建图的邻接矩阵
        #即([row_indices/i]，column_indices[i])对应的位置为1
        mask[row_indices, column_indices] = 1
        if self.cuda:
            mask = mask.cuda()
        
        #统计每一个节点的邻居数量
        num_neigh = mask.sum(1, keepdim=True)
        #归一化（除以邻居数量）
        mask = mask.div(num_neigh)
        if self.cuda:
            embed_matrix = self.features(torch.LongTensor(unique_nodes_list).cuda())
        else:
            embed_matrix = self.features(torch.LongTensor(unique_nodes_list))
        
        #mask是nodes*unique_nodes大小的“邻接矩阵"（batch的邻接矩阵比原始邻接矩阵行列都变小了），embed_matrix是unique nodes*hid size的“特征矩阵”（batch的特征矩阵比原始特征矩阵行变小了）
        #即A*x，这里A是邻接矩阵，x是特征矩阵，这里一系列的操作是按batch训练需要采样出一个局部的A、x
        to_feats = mask.mm(embed_matrix)
        return to_feats

encoders.py

import torch
import torch.nn as nn
from torch.nn import init
import torch.nn.functional as F

class Encoder(nn.Module):
    """
    Encodes a node's using 'convolutional' GraphSage approach
    """
    def __init__(self, features, feature_dim, 
            embed_dim, adj_lists, aggregator,
            num_sample=10,
            base_model=None, gcn=False, cuda=False, 
            feature_transform=False): 
        super(Encoder, self).__init__()

        self.features = features
        #变换前的hidden_size/维度
        self.feat_dim = feature_dim
        self.adj_lists = adj_lists
        #即邻居聚合后的embedding:agg1=MeanAggregator(features，cuda=True)
        self.aggregator = aggregator
        self.num_sample = num_sample
        if base_model != None:
            self.base_model = base_model

        self.gcn = gcn#默认False，就是要加入节点自身消息
        self.embed_dim = embed_dim#变换后的hidden_size/维度
        self.cuda = cuda
        self.aggregator.cuda = cuda
        #矩阵w维度=变换后维度*变换前维度
        #其中gcn表示是否拼接自身节点信息，如果拼接的话：“自身向量||邻居聚合向量”，所以变换前维度为2倍feat_dim
        #这里的weight对应原文算法1中第五行的Wk
        self.weight = nn.Parameter(torch.FloatTensor(embed_dim, self.feat_dim if self.gcn else 2 * self.feat_dim))
        init.xavier_uniform(self.weight)

    def forward(self, nodes):
        """
        Generates embeddings for a batch of nodes.
        nodes     -- list of nodes
        """
        #调用aggregator.py文件中的MeanAggregator class的forward函数，得到聚合邻居的信息，相当于算法1中第五行去调用第四行
        neigh_feats = self.aggregator.forward(nodes, [self.adj_lists[int(node)] for node in nodes], 
                self.num_sample)
        if not self.gcn:
            if self.cuda:
                self_feats = self.features(torch.LongTensor(nodes).cuda())
            else:
                self_feats = self.features(torch.LongTensor(nodes))
            #将自身和聚合邻居的向量按行拼接，对应算法1第五行
            combined = torch.cat([self_feats, neigh_feats], dim=1)
        else:# 不用自身信息进行聚合
            combined = neigh_feats
        #送入到神经网络，algorithm 1第五行：乘以矩阵W_k
        combined = F.relu(self.weight.mm(combined.t()))
        #经过一层GNN layer后的点的embedding，维度为embed_dim*nodes
        return combined

6作业

【思考题】将实践的代码与论文中的公式对应起来，回顾模型是如何实现的。
【代码实践】为算法设置不同的参数，如hidden_size的维度（128）、num_samples（5）的大小，评估对模型效果的影响。
【代码实践】尝试3层GNN Layer代码的改写，以及效果的展示。
【代码实践】思考其他aggregator的实现方式，如LSTM、pooling等，可参考DGL或wiliam code的tensorflow版本。
【总结】总结graphSAGE的关键技术以及如何代码实现。