(五十三)论文阅读 | 轻量级网络之RepVGG
简介
论文提出一种简单高效的卷积神经网络,该模型的推理结构类似于 V G G {\rm VGG} VGG,训练模型使用多分支结构。 论文原文 源码
0. Abstract
论文提出一种简单高效的卷积神经网络,该模型的推理结构类似于 V G G {\rm VGG} VGG,训练模型使用多分支结构。通过结构再参数化技术实现训练结构和推理结构的解耦,得到模型 R e p V G G {\rm RepVGG} RepVGG。
论文贡献:(一)论文提出的 R e p V G G {\rm RepVGG} RepVGG达到实时性 S O T A {\rm SOTA} SOTA;(二)论文提出使用结构再参数技术将训练结构解耦成推理结构;(三)实验证明了 R e p V G G {\rm RepVGG} RepVGG在图像分类和语义分割等任务上的有效性。
1. Introduction
尽管复杂模型有着比简单模型更高的精度,其缺点也很明显:(1)复杂的多分支设计使其难以实现和自定义模型,从而减缓了推理速度,降低了内存利用率;(2)某些如深度卷积和通道混洗等模块增加了内存访问代价和难以支持不同设备。由于影响推理速度的因素太多,浮点运算次数( F L O P s {\rm FLOPs} FLOPs)并不能准确反应模型的实际速度。尽管某些模型有着比经典模型如 V G G {\rm VGG} VGG等更小的 F L O P s {\rm FLOPs} FLOPs,但它们的推理速度可能不会更快。
论文提出一种类似于 V G G {\rm VGG} VGG的结构,其特点如下:(1)该模型拥有与 V G G {\rm VGG} VGG类似的直筒式结构;(2)模型主体仅使用 3 × 3 3\times3 3×3卷积和 R e L U {\rm ReLU} ReLU;(3)没有使用自动搜索、复合缩放等繁琐的操作。
对于普通模型来说,要达到与多分支结构相当的性能水平具有很大的挑战性,一种解释是后者可以避免梯度的消失。
由于多分支结构的优点是利于训练,而不利于推理,论文提出使用结构再参数化来解耦训练时使用的多分支结构,而在推理时使用普通结构,这就意味着需要通过转换将其参数从一种结构转换到另一种。具体而言,网络结构与一组参数耦合,如使用四阶张量表示卷积层。如果可以将某个结构的参数转换为另一结构耦合的另一组参数,则可以用后者等效地替换前者,从而更改整个网络结构。
具体地,基于 1 × 1 {\rm 1\times1} 1×1分支结构来构建训练模型,推理时的分支结构通过再参数化来移除。训练完成后,使用简单的代数运算完成转换。如恒等分支可以看作是退化的 1 × 1 {\rm 1\times1} 1×1卷积,而普通的 1 × 1 {\rm 1\times1} 1×1卷积又可以看作是退化的 3 × 3 {\rm 3\times3} 3×3卷积。所以,可以使用训练好的 3 × 3 {\rm 3\times3} 3×3卷积、恒等连接、 1 × 1 {\rm 1\times1} 1×1卷积和 B N {\rm BN} BN的参数来构建一个新的 3 × 3 {\rm 3\times3} 3×3卷积。因此,转换后的模型由堆叠的 3 × 3 {\rm 3\times3} 3×3卷积组成,以此便于推理和部署。
值得注意的是,用于推理的 R e p V G G {\rm RepVGG} RepVGG仅包含 3 × 3 {\rm 3\times3} 3×3卷积和 R e L U {\rm ReLU} ReLU,这使其可以在 G P U s {\rm GPUs} GPUs等通用设备上快速运行。甚至, R e p V G G {\rm RepVGG} RepVGG能为专门的硬件实现更快的运行速度,因为考虑到芯片的大小和功耗,所需要的操作类型也就越少,即可以集成到芯片上的计算单元就越多。
2. Related Work
2.1 From Single-path to Multi-branch
该部分介绍了自 R e p V G G {\rm RepVGG} RepVGG以来出现了许多优秀的图像分类模型,而后基于神经架构搜索技术得到具有更高性能的模型。一些基于 N A S {\rm NAS} NAS的模型尽管有着高精度等特点,但是复杂的结构使其难以在常规 G P U {\rm GPU} GPU上训练,从而限制了模型的应用场景。此外,复杂的模型会降低计算的并行性,从而降低其推理速度。
2.2 Effective Training of Single-path Models
前人工作尝试设计没有分支结构的神经网络,通常基于更深的深度来获得接近于复杂模型的精度,这类模型既不简单也不实用。如基于平均场论得到一个一万层的神经网络,在 M N I S T {\rm MNIST} MNIST上得到 99 % {\rm 99\%} 99%的结果,在 C I F A R 10 {\rm CIFAR10} CIFAR10上得到 82 % {\rm 82\%} 82%的结果。尽管该模型不具有实际作用,但其具有极大的理论贡献。近来,结合 L e a k y R e L U {\rm Leaky\ ReLU} Leaky ReLU、 m a x {\rm max} max- n o r m {\rm norm} norm和良好的初始化得到的普通模型的参数量为 147 M {\rm 147M} 147M,精度为 74.6 % {\rm 74.6\%} 74.6%,低于 R e s N e t 101 {\rm ResNet101} ResNet101的 76.6 % {\rm 76.6\%} 76.6%、 45 M {\rm 45M} 45M。总之,在参数量相当的情况下,普通模型的精度大大低于复杂模型。
论文的目标是利用常见的组件(如卷积和批量归一化)和简单的代数运算来构建一个简单的模型,其具有合适的深度和在速度和精度之间具有良好的平衡。
2.3 Model Re-parameterization
D i r a c N e t {\rm DiracNet} DiracNet基于再参数化得到,它将卷积核 W ^ = d i a g ( a ) I + d i a g ( b ) W n o r m {\rm \hat W={\rm diag(a)}I+{\rm diag}(b)W_{norm}} W^=diag(a)I+diag(b)Wnorm进行编码。与相当参数量的 R e s N e t {\rm ResNet} ResNet相比,在 C I F A R 100 {\rm CIFAR100} CIFAR100和 I m a g e N e t {\rm ImageNet} ImageNet的实验上,前者的精度分别低于后者 2.29 % {\rm 2.29\%} 2.29%和 0.62 % {\rm 0.62\%} 0.62%。 D i r a c N e t {\rm DiracNet} DiracNet与 R e p V G G {\rm RepVGG} RepVGG不同的是:(1) R e p V G G {\rm RepVGG} RepVGG的结构再参数化技术是通过一个具体结构的数据流来实现的,该结构后续被转换成另一个结构,而 D i r a c N e t {\rm DiracNet} DiracNet仅使用卷积核的另一个数学表达来简化优化操作;(2) D i r a c N e t {\rm DiracNet} DiracNet的精度高于普通模型,但是低于相当参数的 R e s N e t {\rm ResNet} ResNet,而 R e p V G G {\rm RepVGG} RepVGG大幅高于 R e s N e t {\rm ResNet} ResNet。非对称卷积模型( A C B {\rm ACB} ACB)采用非对称的卷积来增强卷积结构,这可以看作是结构再参数化的另一种形式,即将训练的模块转换成卷积层。与 R e p V G G {\rm RepVGG} RepVGG不同的是, A C B {\rm ACB} ACB是为了组件级改进和作为卷积层的替代而设计的,而论文所使用的结构再参数化针对普通卷积网络的训练。
2.4 Winograd Convolution
受益于英伟达 c u D N N {\rm cuDNN} cuDNN和英特尔 M K L {\rm MKL} MKL等在 C P U {\rm CPU} CPU和 G P U {\rm GPU} GPU上的优化, R e p V G G {\rm RepVGG} RepVGG仅使用 3 × 3 {\rm 3\times3} 3×3卷积。

由上图可以看到, 3 × 3 {\rm 3\times3} 3×3卷积的每秒浮点运算次数( T F L O P S {\rm TFLOPS} TFLOPS)大大高于其他形式的卷积。而 3 × 3 {\rm 3\times3} 3×3卷积使用的经典加速方法为 W i n o g r a d {\rm Winograd} Winograd算法(步长为 1 {\rm 1} 1),这在 c u D N N {\rm cuDNN} cuDNN和 M K L {\rm MKL} MKL中均已得到实现。例如,对于标准的 W i n o g r a d {\rm Winograd} Winograd为 F ( 2 × 2 , 3 × 3 ) F(2\times2,3\times3) F(2×2,3×3)而言, 3 × 3 {\rm 3\times3} 3×3卷积的乘法运算次数是普通实现方式的 4 / 9 4/9 4/9。而在计算机中,乘法的实现代价相比于加法更高,所以通常又以乘法运算次数来衡量模型的计算代价。
3. Building RepVGG via Structural Re-param
3.1 Simple is Fast, Memory-economical, Flexible
简单卷积神经网络的特点主要如下:快速,节约内存和灵活。
许多多分支尽管有着比 V G G {\rm VGG} VGG更低的理论 F L O P s {\rm FLOPs} FLOPs,但其运行速度却不如后者。除了加速算法 W i n o g r a d {\rm Winograd} Winograd, F L O P s {\rm FLOPs} FLOPs与速度之间的差异可归因于两个重要因素:内存访问代价( M A C {\rm MAC} MAC)和计算的并行度。多分支结构在 I n c e p t i o n {\rm Inception} Inception和自动架构中应用广泛,其通常使用多个小算子来代替若干个大算子。
多分支拓扑结构的内存效率底下,因为每个分支的结果都需要保存以后续用以相加或拼接,从而提高了内存占用的峰值。假设块的大小为输入大小,则其内存峰值为输入的两倍。相对应的,对于普通模型来说,当某一层的操作完成后,其占用的内存会被立即释放。对于特定的软件来说,普通卷积神经网络能够对内存使用的优化进行深度优化,减少内存代价从而使得我们可以在芯片上集成更多的计算单元。
多分支结构对于模型结构的设计有着制约作用,更有甚者限制了通道的剪枝等优化操作。相对应的,普通结构使我们可以根据需求自由地配置每个卷积层,从而使用剪枝等使模型在性能和效率之间获得平衡。
3.2 Training-time Multi-branch Architecture
普通模型有许多优点,但其最大的缺点是精度低。论文的结构再参数化基于 R e s N e t {\rm ResNet} ResNet,其可以表示为 y = x + f ( x ) y=x+f(x) y=x+f(x),其中 f f f表示残差模块。当 x x x和 f ( x ) f(x) f(x)的维度不匹配是,则上式表示为 y = g ( x ) + f ( x ) y=g(x)+f(x) y=g(x)+f(x),其中 g ( x ) g(x) g(x)表示 1 × 1 1\times1 1×1卷积。对于 R e s N e t {\rm ResNet} ResNet成功的一个解释是,其分支结构使模型可以看作是许多浅层模型的隐式集合。具体地,对于 n n n个模块,该模型可以解释为 2 n 2^n 2n个模型的集合,这里的每个块有两条分支。
由于多分支结构适用于训练,而不适用于推理,因此论文将多分支结构仅用于训练。论文构建的结构是 y = x + g ( x ) + f ( x ) y=x+g(x)+f(x) y=x+g(x)+f(x),然后简单地堆叠该结构后得到最终的模型。这里,可以解释为 3 n 3^n 3n个模型的集合。训练完成后,其被转换成 y = h ( x ) y=h(x) y=h(x),其中 h h h表示单个卷积层,其参数来自于代数转换后的训练参数。
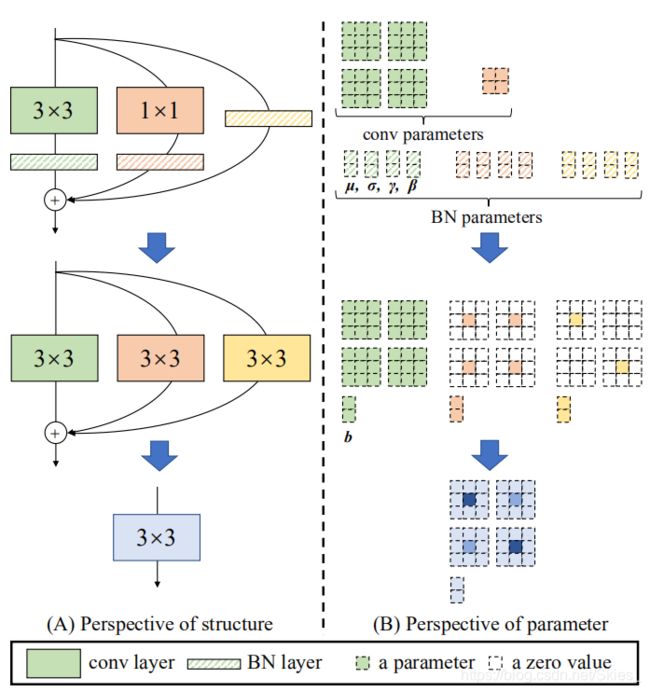
3.3 Re-param for Plain Inference-time Model
该部分介绍如何将训练模块转换成一个 3 × 3 3\times3 3×3卷积层,从而将其用于模型推理。这里,使用 W ( 3 ) ∈ R C 2 × C 1 × 3 × 3 {\rm W}^{(3)}\in \mathbb R^{C_2\times C_1\times3\times3} W(3)∈RC2×C1×3×3表示 3 × 3 3\times3 3×3卷积, W ( 1 ) ∈ R C 2 × C 1 {\rm W}^{(1)}\in \mathbb R^{C_2\times C_1} W(1)∈RC2×C1表示 1 × 1 1\times1 1×1分支。使用 μ ( 3 ) , σ ( 3 ) , γ ( 3 ) , β ( 3 ) \mu^{(3)},\sigma^{(3)},\gamma^{(3)},\beta^{(3)} μ(3),σ(3),γ(3),β(3)表示 3 × 3 3\times3 3×3卷积的累计平均值,标准差以及 B N {\rm BN} BN层所学习到的缩放系数和偏置; μ ( 1 ) , σ ( 1 ) , γ ( 1 ) , β ( 1 ) \mu^{(1)},\sigma^{(1)},\gamma^{(1)},\beta^{(1)} μ(1),σ(1),γ(1),β(1)表示 1 × 1 1\times1 1×1卷积的对应值; μ ( 0 ) , σ ( 0 ) , γ ( 0 ) , β ( 0 ) \mu^{(0)},\sigma^{(0)},\gamma^{(0)},\beta^{(0)} μ(0),σ(0),γ(0),β(0)分别表示恒等连接的对应值。使用 M ( 1 ) ∈ R N × C 1 × H 1 × W 1 {\rm M}^{(1)}\in \mathbb R^{N\times C_1\times H_1\times W_1} M(1)∈RN×C1×H1×W1和 M ( 2 ) ∈ R N × C 2 × H 2 × W 2 {\rm M}^{(2)}\in \mathbb R^{N\times C_2\times H_2\times W_2} M(2)∈RN×C2×H2×W2分别表示输入和输出, ∗ * ∗表示卷积操作。如果 C 1 = C 2 , H 1 = H 2 , W 1 = W 2 C_1=C_2,H_1=H_2,W_1=W_2 C1=C2,H1=H2,W1=W2,则有:
M ( 2 ) = b n ( M ( 1 ) ∗ W ( 3 ) , μ ( 3 ) , σ ( 3 ) , γ ( 3 ) , β ( 3 ) ) + b n ( M ( 1 ) ∗ W ( 1 ) , μ ( 1 ) , σ ( 1 ) , γ ( 1 ) , β ( 1 ) ) + b n ( M ( 1 ) , μ ( 0 ) , σ ( 0 ) , γ ( 0 ) , β ( 0 ) ) . (1) \begin{aligned} \rm M^{(2)}&=\rm bn(M^{(1)}*W^{(3)},\mu^{(3)},\sigma^{(3)},\gamma^{(3)},\beta^{(3)}) \\ &+\rm bn(M^{(1)}*W^{(1)},\mu^{(1)},\sigma^{(1)},\gamma^{(1)},\beta^{(1)}) \\ & +\rm bn(M^{(1)},\mu^{(0)},\sigma^{(0)},\gamma^{(0)},\beta^{(0)}). \end{aligned}\tag{1} M(2)=bn(M(1)∗W(3),μ(3),σ(3),γ(3),β(3))+bn(M(1)∗W(1),μ(1),σ(1),γ(1),β(1))+bn(M(1),μ(0),σ(0),γ(0),β(0)).(1)
否则,使用没有恒等连接的结构,上式仅有前两项。这里, b n {\rm bn} bn表示推理时使用的 B N {\rm BN} BN,通常,对于 ∀ 1 ≤ i ≤ C 2 \forall 1\leq i\leq C_2 ∀1≤i≤C2,有(即 B N {\rm BN} BN的计算公式): b n = ( M , μ , σ , γ , β ) : , i , : , : = ( M : , i , : , : − μ i ) γ i σ i + β i (2) {\rm bn=(M,\mu,\sigma,\gamma,\beta)}_{:,i,:,:}={\rm (M}_{:,i,:,:}-\mu_i)\frac{\gamma_i}{\sigma_i}+\beta_i\tag{2} bn=(M,μ,σ,γ,β):,i,:,:=(M:,i,:,:−μi)σiγi+βi(2)
首先,将 B N {\rm BN} BN和其之前的卷积层转换成一个带偏置的卷积向量。令 { W ′ , b ′ } \{\rm W',b'\} {W′,b′}表示转换自 { W , μ , σ , γ , β } \{\rm W,\mu,\sigma,\gamma,\beta\} {W,μ,σ,γ,β}卷积和偏置,有(即将上式右端拆开): W i , : , : , : ′ = γ i σ i W i , : , : , : , b i ′ = − μ i γ i σ i + β i (3) {\rm W}'_{i,:,:,:}=\frac{\gamma_i}{\sigma_i}{\rm W}_{i,:,:,:},\ \ {\rm b}_i'=-\frac{\mu_i\gamma_i}{\sigma_i}+\beta_i\tag{3} Wi,:,:,:′=σiγiWi,:,:,:, bi′=−σiμiγi+βi(3)
容易得证,对于 ∀ 1 ≤ i ≤ C 2 \forall1\leq i\leq C_2 ∀1≤i≤C2: b n ( M ∗ W , μ , σ , γ , β ) : , i : , : = M ∗ W ′ : , i , : , : + b i ′ (4) {\rm bn(M*W,\mu,\sigma,\gamma,\beta)}_{:,i:,:}={\rm M*W'}_{:,i,:,:}+{\rm b}_i'\tag{4} bn(M∗W,μ,σ,γ,β):,i:,:=M∗W′:,i,:,:+bi′(4)
上式转换也适用于恒等连接,因为其可以看作是 1 × 1 1\times1 1×1卷积。经过上述转换,我们可以得到一个 3 × 3 3\times3 3×3卷积,两个 1 × 1 1\times1 1×1卷积和三个表示偏置的向量。然后,将三个偏置向量相加得到最后的偏置参数,然后使用零填充将 1 × 1 1\times1 1×1卷积填充为 3 × 3 3\times3 3×3大小,最后将所有 3 × 3 3\times3 3×3大小的卷积相加,得到最后的卷积参数。
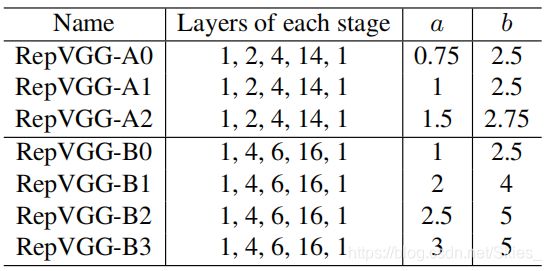
3.4 Architectural Specification
上图中的 a a a和 b b b表示通道的缩放系数。
4. Experiments
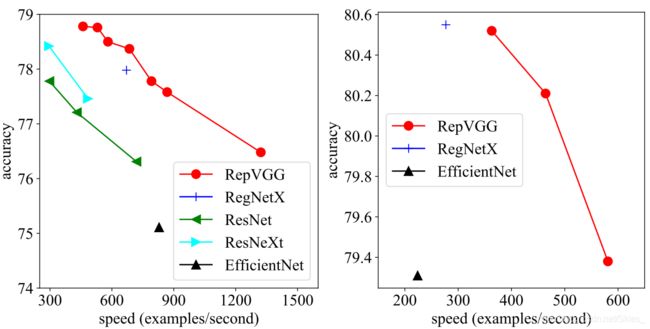
4.1 RepVGG for ImageNet Classification
4.2 Structural Re-parameterization is the Key
I d e n t i t y w / o B N {\rm Identity\ w/o\ BN} Identity w/o BN表示移除恒等连接分支的 B N {\rm BN} BN
P o s t − a d d i t i o n B N {\rm Post-addition\ BN} Post−addition BN表示移除所有层的 B N {\rm BN} BN,然后在相加后使用 B N {\rm BN} BN层
+ R e L U i n b r a n c h e s {\rm +ReLU\ in\ branches} +ReLU in branches表示在每层插入 R e L U {\rm ReLU} ReLU层
D i r a c N e t {\rm DiracNet} DiracNet
T r i v i a l R e − p a r a m {\rm Trivial\ Re-param} Trivial Re−param 简单的再参数化,即直接将恒等连接相加到 3 × 3 {\rm 3\times3} 3×3卷积
A C B {\rm ACB} ACB即非对称卷积模块
R e s i d u a l R e o r g {\rm Residual\ Reorg} Residual Reorg表示按照 R e s N e t {\rm ResNet} ResNet的形式构建 R e p V G G {\rm RepVGG} RepVGG的每个阶段
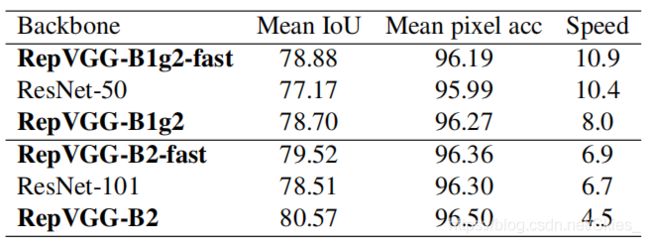
4.3 Semantic Segmentation
4.4 Limitations
R e p V G G {\rm RepVGG} RepVGG是一种简单快速、实用性强的模型,具有较少的参数和较低的 F L O P s {\rm FLOPs} FLOPs。尽管 R e p V G G {\rm RepVGG} RepVGG的参数比 R e s N e t {\rm ResNet} ResNet更加高效,但其不如轻量级网络如 M o b i l e N e t s {\rm MobileNets} MobileNets和 S h u f f l e N e t s {\rm ShuffleNets} ShuffleNets等在移动端上的表现。
5. Conclusion
论文提出 R e p V G G {\rm RepVGG} RepVGG,它仅由 3 × 3 3\times3 3×3卷积和 R e L U {\rm ReLU} ReLU组成,从而使其方便用于 G P U {\rm GPU} GPU等。
6. PyTorch实现RepVGG
R e p V G G {\rm RepVGG} RepVGG模块的构建:
class RepVGGBlock(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, padding_mode='zeros', deploy=False):
super(RepVGGBlock, self).__init__()
self.deploy = deploy
self.groups = groups
self.in_channels = in_channels
assert kernel_size == 3
assert padding == 1
padding_11 = padding - kernel_size // 2
self.nonlinearity = nn.ReLU()
# 根据deploy决定构建训练模型还是推理模型
if deploy:
# 推理时仅有一个3x3卷积
self.rbr_reparam = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=stride, padding=padding, dilation=dilation, groups=groups, bias=True, padding_mode=padding_mode)
else:
# 训练时包含一个恒等连接、一个3x3卷积核一个1x1卷积
self.rbr_identity = nn.BatchNorm2d(num_features=in_channels) if out_channels == in_channels and stride == 1 else None
self.rbr_dense = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=stride, padding=padding, groups=groups)
self.rbr_1x1 = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=1, stride=stride, padding=padding_11, groups=groups)
print('RepVGG Block, identity = ', self.rbr_identity)
def forward(self, inputs):
if hasattr(self, 'rbr_reparam'):
return self.nonlinearity(self.rbr_reparam(inputs))
if self.rbr_identity is None:
id_out = 0
else:
id_out = self.rbr_identity(inputs)
return self.nonlinearity(self.rbr_dense(inputs) + self.rbr_1x1(inputs) + id_out)
# 核和偏置的转换,具体实现在_fuse_bn_tensor函数
def get_equivalent_kernel_bias(self):
kernel3x3, bias3x3 = self._fuse_bn_tensor(self.rbr_dense)
kernel1x1, bias1x1 = self._fuse_bn_tensor(self.rbr_1x1)
kernelid, biasid = self._fuse_bn_tensor(self.rbr_identity)
# 核和偏置合并
return kernel3x3 + self._pad_1x1_to_3x3_tensor(kernel1x1) + kernelid, bias3x3 + bias1x1 + biasid
def _pad_1x1_to_3x3_tensor(self, kernel1x1):
if kernel1x1 is None:
return 0
else:
return torch.nn.functional.pad(kernel1x1, [1,1,1,1])
def _fuse_bn_tensor(self, branch):
if branch is None:
return 0, 0
if isinstance(branch, nn.Sequential):
# 卷积层权重
kernel = branch.conv.weight
# μ
running_mean = branch.bn.running_mean
# σ
running_var = branch.bn.running_var
# BN层权重
gamma = branch.bn.weight
# BN层偏置
beta = branch.bn.bias
# BN层防止除零的参数
eps = branch.bn.eps
else:
assert isinstance(branch, nn.BatchNorm2d)
if not hasattr(self, 'id_tensor'):
input_dim = self.in_channels // self.groups
kernel_value = np.zeros((self.in_channels, input_dim, 3, 3), dtype=np.float32)
for i in range(self.in_channels):
kernel_value[i, i % input_dim, 1, 1] = 1
self.id_tensor = torch.from_numpy(kernel_value).to(branch.weight.device)
kernel = self.id_tensor
running_mean = branch.running_mean
running_var = branch.running_var
gamma = branch.weight
beta = branch.bias
eps = branch.eps
std = (running_var + eps).sqrt()
t = (gamma / std).reshape(-1, 1, 1, 1)
# 式(3),返回 W'和 b'
return kernel * t, beta - running_mean * gamma / std
def repvgg_convert(self):
kernel, bias = self.get_equivalent_kernel_bias()
return kernel.detach().cpu().numpy(), bias.detach().cpu().numpy(),
R e p V G G {\rm RepVGG} RepVGG主体部分的构建:
class RepVGG(nn.Module):
def __init__(self, num_blocks, num_classes=1000, width_multiplier=None, override_groups_map=None, deploy=False):
super(RepVGG, self).__init__()
assert len(width_multiplier) == 4
self.deploy = deploy
self.override_groups_map = override_groups_map or dict()
assert 0 not in self.override_groups_map
self.in_planes = min(64, int(64 * width_multiplier[0]))
# 构建RepVGG的各阶段
self.stage0 = RepVGGBlock(in_channels=3, out_channels=self.in_planes, kernel_size=3, stride=2, padding=1, deploy=self.deploy)
self.cur_layer_idx = 1
self.stage1 = self._make_stage(int(64 * width_multiplier[0]), num_blocks[0], stride=2)
self.stage2 = self._make_stage(int(128 * width_multiplier[1]), num_blocks[1], stride=2)
self.stage3 = self._make_stage(int(256 * width_multiplier[2]), num_blocks[2], stride=2)
self.stage4 = self._make_stage(int(512 * width_multiplier[3]), num_blocks[3], stride=2)
self.gap = nn.AdaptiveAvgPool2d(output_size=1)
# 用于分类的全连接层
self.linear = nn.Linear(int(512 * width_multiplier[3]), num_classes)
def _make_stage(self, planes, num_blocks, stride):
strides = [stride] + [1]*(num_blocks-1)
blocks = []
for stride in strides:
cur_groups = self.override_groups_map.get(self.cur_layer_idx, 1)
blocks.append(RepVGGBlock(in_channels=self.in_planes, out_channels=planes, kernel_size=3,
stride=stride, padding=1, groups=cur_groups, deploy=self.deploy))
self.in_planes = planes
self.cur_layer_idx += 1
return nn.Sequential(*blocks)
def forward(self, x):
out = self.stage0(x)
out = self.stage1(out)
out = self.stage2(out)
out = self.stage3(out)
out = self.stage4(out)
out = self.gap(out)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
以下函数的作用是基于 R e p V G G {\rm RepVGG} RepVGG构建用于分类和分割等任务的模型,并返回推理模型:
def whole_model_convert(train_model:torch.nn.Module, deploy_model:torch.nn.Module, save_path=None):
all_weights = {}
for name, module in train_model.named_modules():
# 条件语句判断不同形式的层
if hasattr(module, 'repvgg_convert'):
# 获得转换后的卷积层权重和偏置
kernel, bias = module.repvgg_convert()
# 加载权重
all_weights[name + '.rbr_reparam.weight'] = kernel
all_weights[name + '.rbr_reparam.bias'] = bias
print('convert RepVGG block')
else:
for p_name, p_tensor in module.named_parameters():
full_name = name + '.' + p_name
if full_name not in all_weights:
all_weights[full_name] = p_tensor.detach().cpu().numpy()
for p_name, p_tensor in module.named_buffers():
full_name = name + '.' + p_name
if full_name not in all_weights:
all_weights[full_name] = p_tensor.cpu().numpy()
# 加载权重
deploy_model.load_state_dict(all_weights)
if save_path is not None:
torch.save(deploy_model.state_dict(), save_path)
return deploy_model
用法:
# 1. 构建基于RepVGG的任务模型,如这里构建PSPNet
# 2. 构建PSPNet的推理模型
# 调用流程如下:
###################### 1 ######################
train_backbone = create_RepVGG_B2(deploy=False)
train_backbone.load_state_dict(torch.load('RepVGG-B2-train.pth'))
train_pspnet = build_pspnet(backbone=train_backbone)
segmentation_train(train_pspnet)
###################### 2 ######################
deploy_backbone = create_RepVGG_B2(deploy=True)
deploy_pspnet = build_pspnet(backbone=deploy_backbone)
whole_model_convert(train_pspnet, deploy_pspnet)
segmentation_test(deploy_pspnet)
以下函数的作用是将 R e p V G G {\rm RepVGG} RepVGG转换成推理模型:
def repvgg_model_convert(model:torch.nn.Module, build_func, save_path=None):
converted_weights = {}
for name, module in model.named_modules():
if hasattr(module, 'repvgg_convert'):
kernel, bias = module.repvgg_convert()
converted_weights[name + '.rbr_reparam.weight'] = kernel
converted_weights[name + '.rbr_reparam.bias'] = bias
elif isinstance(module, torch.nn.Linear):
converted_weights[name + '.weight'] = module.weight.detach().cpu().numpy()
converted_weights[name + '.bias'] = module.bias.detach().cpu().numpy()
del model
deploy_model = build_func(deploy=True)
for name, param in deploy_model.named_parameters():
print('deploy param: ', name, param.size(), np.mean(converted_weights[name]))
param.data = torch.from_numpy(converted_weights[name]).float()
if save_path is not None:
torch.save(deploy_model.state_dict(), save_path)
return deploy_model
用法:
# 构建模型
train_model = create_RepVGG_A0(deploy=False)
# 训练模型
train train_model
# 转换模型
deploy_model = repvgg_convert(train_model, create_RepVGG_A0, save_path='repvgg_deploy.pth')
参考
- Ding X, Zhang X, Ma N, et al. RepVGG: Making VGG-style ConvNets Great Again[J]. arXiv preprint arXiv:2101.03697, 2021.