Python数据分析之Matplotlib

1.简介:

Matplotlib是一个用来可视化的第三方工具包.
我们在使用这个包之前需要先将其下载到Python解释器中,使用pip即可.
下载命令:

pip install matplotlib

因为使用matplotlib,一定会使用numpy,所以也得提前准备好numpy
numpy是科学计算库,经常用来计算矩阵等

pip install numpy

2.使用

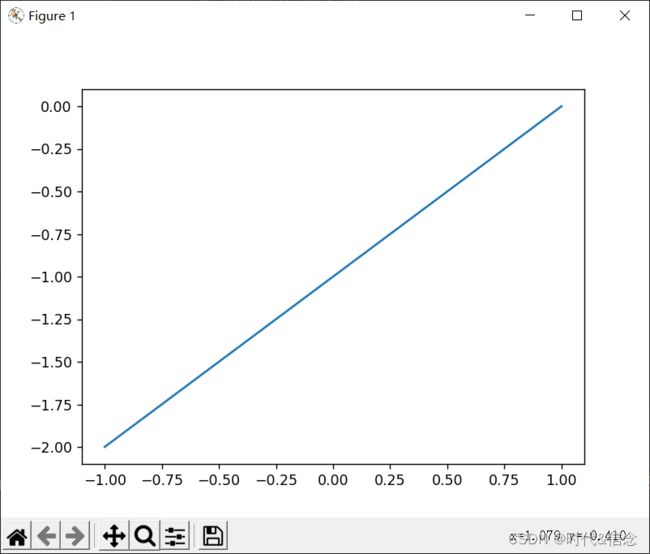
(1)绘制直线

代码:

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt

"""
    绘制一条直线
"""

# 通过numpy创造50个数据，范围为从-1到1
x = np.linspace(-1, 1, 50)
# y值
y = x - 1
# 通过自变量和因变量进行绘制
plt.plot(x, y)
# 进行展示
plt.show()

效果展示:

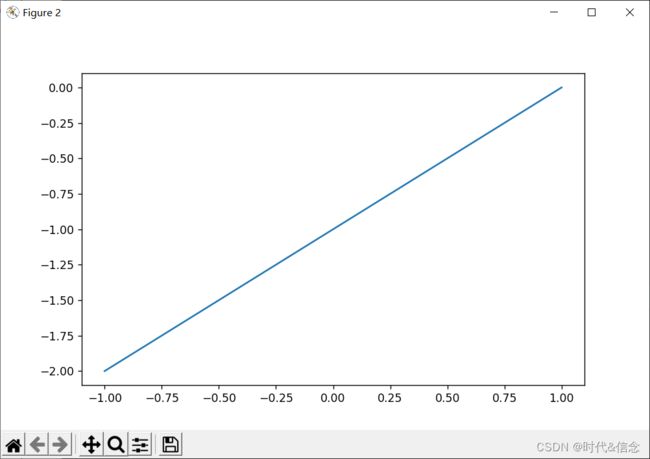
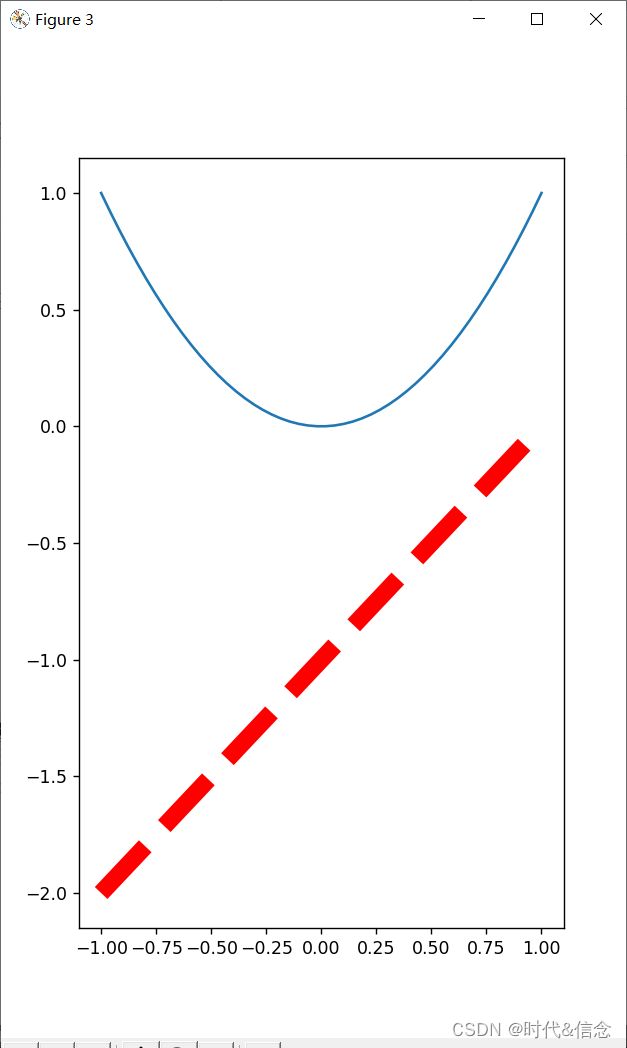
(2)figure的使用

代码:

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt

"""
    figure的使用
"""

# 造数据, 在-1~1之间均匀生成50个数
x = np.linspace(-1, 1, 50)

# 编号为2的图像,通过figsize参数设置图像的大小
plt.figure(num=2, figsize=(8, 5))
y1 = x - 1
# 绘制编号为2的图像
plt.plot(x, y1)


# 编号为3的图像 ,figsize=(宽， 高)
plt.figure(num=3, figsize=(5, 8))
y2 = x**2
# 绘制编号为3的图像，  绘制的有两条
plt.plot(x, y2)
# color参数用来设置线条颜色,linewidth参数用来设定线条宽度,linestyle参数用来设定线条样式
plt.plot(x, y1, color="red", linewidth=10.0, linestyle="--")

# 进行展示
plt.show()

效果展示:

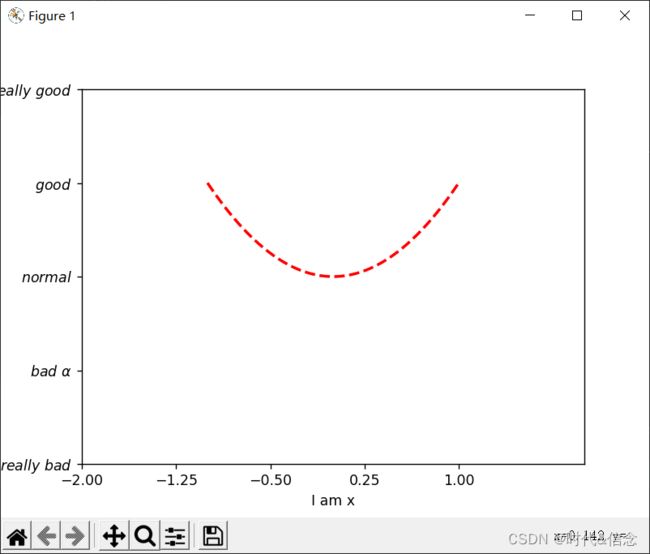
(3)对图像的坐标轴进行设定

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    对图像的坐标轴进行设定
"""

# 造数据, 在-1~1之间均匀生成50个数
x = np.linspace(-1, 1, 50)
y = x**2
plt.plot(x, y, color="red", linewidth=2.0, linestyle="--")
# 设定x的范围
plt.xlim(-2, 2)
# 设定y的范围
plt.ylim(-2, 2)

# 设置x轴描述
plt.xlabel("I am x")
# 设置y轴描述
plt.ylabel("I am y")

# 设置每一格的宽度,参数-2是起始，参数1是终止，参数5是刻度总数
new_ticks = np.linspace(-2, 1, 5)
# print(new_ticks)
# 设定新的横轴刻度
plt.xticks(new_ticks)

# 设定新的纵轴刻度
# 前后加上美元符号，使字体变的好看起来
# 如何打印出数学中的alpha，使用\进行转义
plt.yticks([-2, -1, 0, 1, 2],
           [r"$really\ bad$", r"$bad\ \alpha$", r"$normal$", r"$good$", r"$really\ good$"])

# 进行绘制
plt.show()

效果展示:

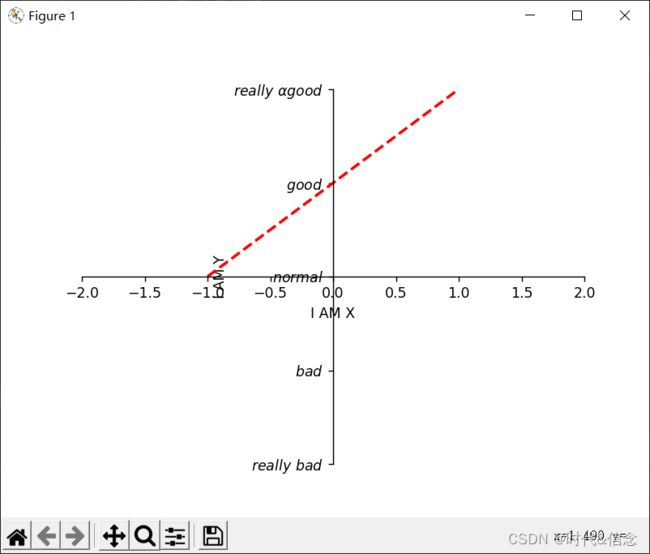
(4)对边框的操作

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    对坐标轴进行设置2
"""

# 造数据
x = np.linspace(-1, 1, 50)
y = x + 1
plt.plot(x, y, color="red", linewidth=2.0, linestyle="--")
# 设置X轴范围
plt.xlim(-2, 2)
# 设置Y轴范围
plt.ylim(-2, 2)
# 设置x轴描述
plt.xlabel("I AM X")
plt.ylabel("I AM Y")

# 重新设置刻度
plt.yticks([-2, -1, 0, 1, 2],
         [r"$really\ bad$", r"$bad$", r"$normal$", r"$good$", r"$really\ \alpha good$"])

# 获取到图像的四个边框
ax = plt.gca()
ax.spines["right"].set_color("none")
ax.spines["top"].set_color("none")

# 将边框设置为x轴和y轴
ax.xaxis.set_ticks_position("bottom")
ax.yaxis.set_ticks_position("left")
# 将下边框移动到数值为0的位置
ax.spines["bottom"].set_position(('data', 0))
# 将左边框移动到数值为0的位置
ax.spines["left"].set_position(("data", 0))

plt.show()

效果展示:

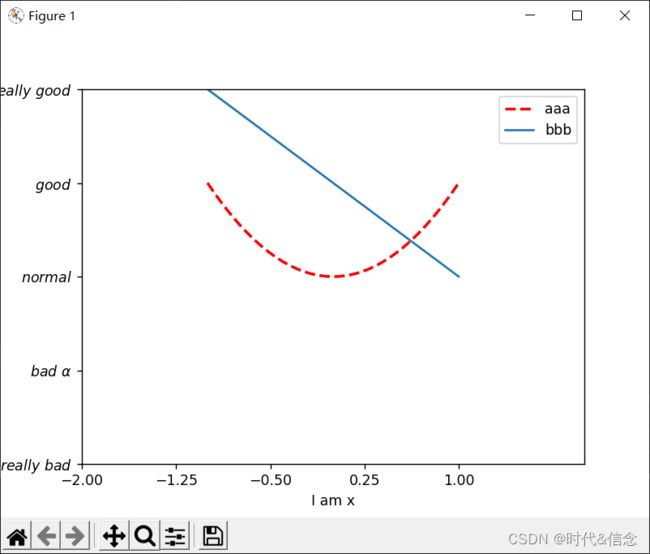
(5)添加图例

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    给图片加上图例legend
"""

# 造数据
x = np.linspace(-1, 1 ,50)
y1 = x**2

# 设定x的范围
plt.xlim(-2, 2)
# 设定y的范围
plt.ylim(-2, 2)

# 设置x轴描述
plt.xlabel("I am x")
# 设置y轴描述
plt.ylabel("I am y")

# 设置每一格的宽度,参数2是起始，参数1是终止，参数5是刻度总数
new_ticks = np.linspace(-2, 1, 5)
# print(new_ticks)
# 设定新的横轴刻度
plt.xticks(new_ticks)

# 设定新的纵轴刻度
# 前后加上美元符号，使字体变的好看起来
# 如何打印出数学中的alpha，使用\进行转义
plt.yticks([-2, -1, 0, 1, 2],
           [r"$really\ bad$", r"$bad\ \alpha$", r"$normal$", r"$good$", r"$really\ good$"])

y2 = -x + 1
# plt.plot(x, y2, label="one")
# # 添加图例
# plt.legend()

l1, = plt.plot(x, y1, color="red", linewidth=2.0, linestyle="--", label="two")
l2, = plt.plot(x, y2, label="one")
# loc="best"表示将自适应最佳的位置
plt.legend(handles=[l1, l2, ], labels=["aaa", "bbb"], loc="best")
# 进行绘制
plt.show()

效果展示:

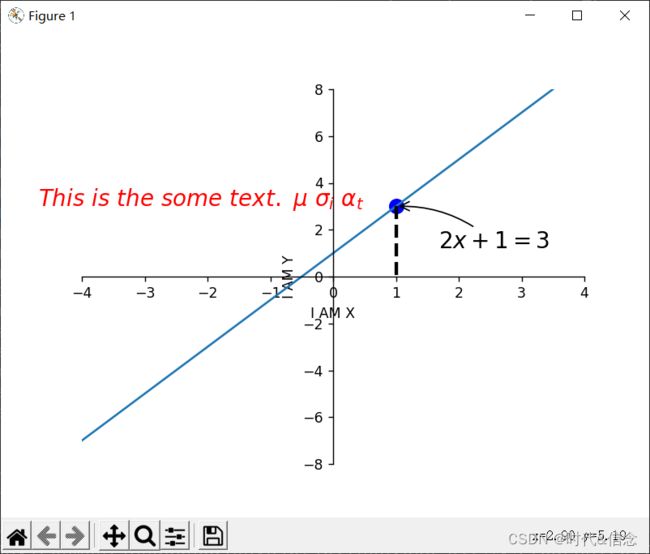
(6)对图片做注释

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    对图片进行标注
"""

# 造数据
x = np.linspace(-5, 5, 20)
y = 2*x + 1
plt.plot(x, y)

# 设定x轴范围
plt.xlim(-4, 4, 9)
# 设定y轴范围
plt.ylim(-8, 8, 9)

# 设定x轴描述
plt.xlabel("I AM X")
# 设定y轴描述
plt.ylabel("I AM Y")

# 获取图像的边框
ax = plt.gca()
ax.spines["right"].set_color("None")
ax.spines["top"].set_color("None")

# 移动剩下的边框
ax.spines["bottom"].set_position(("data", 0))
ax.spines["left"].set_position(("data", 0))

# 展示一个点
x0 = 1
y0 = 2 * x0 + 1
# 标一个点
plt.scatter(x0, y0, color="b", s=100)
plt.plot([x0, x0], [y0, 0], "k--", lw=2.5)

# 进行注释,方式一
plt.annotate(r'$2x+1=%s$' % y0, xy=(x0, y0), xycoords="data", xytext=(+30, -30),
             textcoords="offset points", fontsize=16,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3, rad=.2"))

plt.text(-4.7, 3, r'$This\ is\ the\ some\ text.\ \mu\ \sigma_i\ \alpha_t$',
         fontdict={"size": 16, "color": 'r'})

plt.show()

效果展示:

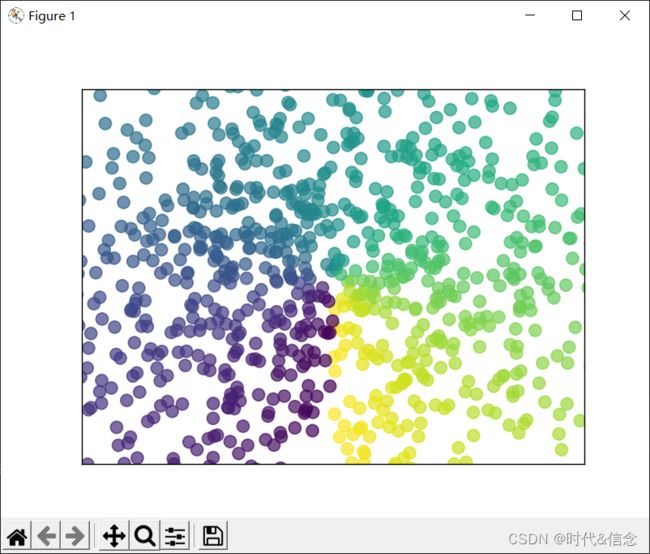
(7)绘制散点图

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    绘制散点图
"""

n = 1024
# 按照正态分布(也叫做高斯分布)生成n个均值为0，标准差为1的随机数
X = np.random.normal(0, 1, n)
Y = np.random.normal(0, 1, n)
# 为了生成颜色
T = np.arctan2(X, Y)

# alpha代表透明度
plt.scatter(X, Y, s=75, c=T, alpha=0.7)
# 设定x轴范围
plt.xlim((-1.5, 1.5))
plt.ylim((-1.5, 1.5))

# 将x轴y轴的数值进行隐藏
plt.xticks(())
plt.yticks(())
# 进行展示
plt.show()

效果展示:

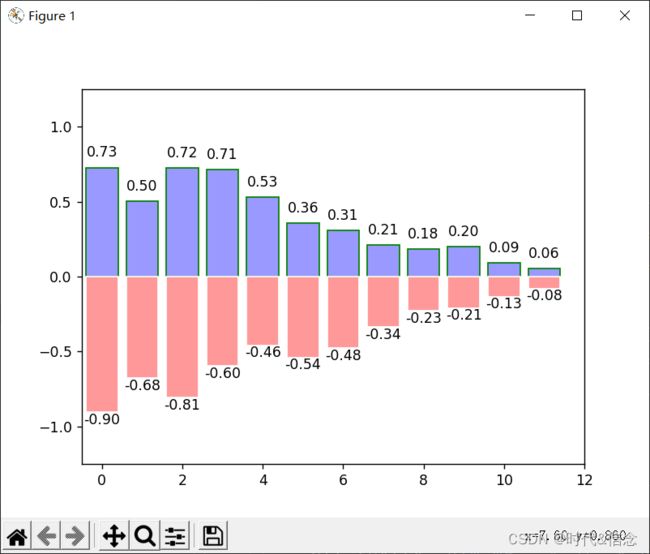
(8)绘制柱状图

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    绘制柱状图
"""

n = 12
X = np.arange(n)
# uniform表示均匀分布,从均匀分布中生成n个,范围为[0.5, 1.0)的随机数!
Y1 = (1-X/float(n))*np.random.uniform(0.5, 1.0, n)
Y2 = (1-X/float(n))*np.random.uniform(0.5, 1.0, n)

# facecolor表示直方颜色,edgecolor表示直方边缘颜色
plt.bar(X, +Y1, facecolor='#9999ff', edgecolor='green')
plt.bar(X, -Y2, facecolor='#ff9999', edgecolor='white')

for x, y in zip(X, Y1):
    # ha:水平方向居中对齐 va:竖直方向向下对齐
    # x，y为文字放置的位置
    plt.text(x, y+0.05, '%.2f' % y, ha="center", va="bottom")

for x, y in zip(X, Y2):
    plt.text(x, -y-0.1, '-%.2f' % y, ha="center", va="bottom")

plt.xlim(-.5, n)
# 消除x轴的数值
# plt.xticks(())
plt.ylim(-1.25, 1.25)
# 消除y轴数值
# plt.yticks(())

plt.show()

效果展示:

(9)绘制等高线

代码:

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt

"""
    等高线的绘制
"""

# 计算高度的函数
def f(x,y):
    return (1- x/2 + x**5 + y**3) * np.exp(-x**2-y**2)


n = 256
# 生成范围为-3~3，生成点的个数为256,间隔均匀
x = np.linspace(-3, 3, n)
# 生成范围为-3~3，生成点的个数为256,间隔均匀
y = np.linspace(-3, 3, n)
# print(x)
# print(y)
# 生成网格点坐标矩阵，通俗的讲就是，将x坐标一个一个对应上y坐标，相当于形成了网格坐标！！！
X, Y = np.meshgrid(x, y)
# print(X)
# print(Y)
# 参数8表示将颜色等级分为10部分。因为为0时，将颜色等级分为了两部分！！！
# cmap表示热力图的形式,
plt.contourf(X, Y, f(X,Y), 8, alpha=0.75, cmap=plt.cm.hot)


# 画等高线的线
C = plt.contour(X,Y, f(X,Y), 8, colors="black", linewidth=.5)

# 给等高线加上数值, inline为True表示数值显示在线里面！！！
plt.clabel(C, inline=True, fontsize=10)
# 去掉x坐标轴
plt.xticks(())
# 去掉y坐标轴
plt.yticks(())
# 展示
plt.show()

效果展示:

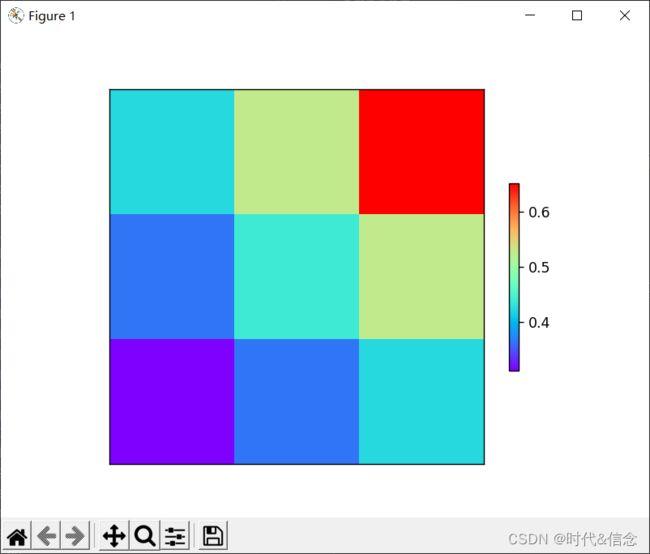
(10)模块数据可视化–图片处理

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    图像image
"""
# 表示把一个一维数组重新生成一个3行3列的二维数组
a = np.array([0.313660827978,0.365348418405,0.423733120134,0.365348418405,0.439599930621,0.525083754405,
0.423733120134,0.525083754405,0.651536351379]).reshape(3,3)

# interpolation表示间隔形式  cmap表示颜色  origin:绘制方向，lower从下向上绘制，upper从上向下绘制
plt.imshow(a, interpolation='nearest', cmap='rainbow', origin='lower')

# shrink参数是将colorbar高度压缩为图像比例的0.5
plt.colorbar(shrink=0.5)

plt.xticks(())
plt.yticks(())
plt.show()

效果展示:

(11)绘制3D图形

代码:

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
"""
    3D图像
"""

fig = plt.figure()
# 添加3D坐标轴
ax = Axes3D(fig)

X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
# 生成网格点坐标矩阵，通俗的讲就是，将x坐标一个一个对应上y坐标，相当于形成了网格坐标！！！
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2+Y**2)

Z = np.sin(R)

# 参数rstride表示行跨，cstride表示列跨
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap("rainbow"))

# zdir参数表示将压到哪个轴    offset参数表示等高线图的平面将压到哪个位置
ax.contourf(X, Y, Z, zdir='z', offset=-1.5, cmap='rainbow')
ax.set_zlim(-2, 2)
plt.show()




# 展示
plt.show()

效果展示:

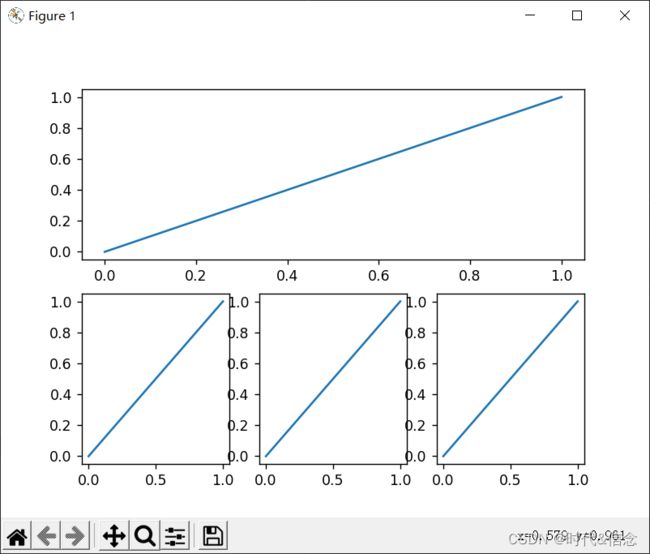
(12)一张大图中放置子图

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    在一张图中放置几张子图
"""

plt.figure()

# 2表示总共两行,1表示当前行只有一列,最后一个类表示图形的计数
plt.subplot(2, 1, 1)
# 第一个列表表示x轴数据,第二个列表表示y轴数据,
plt.plot([0, 1], [0, 1])

# 第一行本该放三个,结果一个图把一行都占了,仍然计数,所以第二行第一列为第四个
plt.subplot(2, 3, 4)
plt.plot([0, 1], [0, 1])

plt.subplot(2, 3, 5)
plt.plot([0, 1], [0, 1])

plt.subplot(2, 3, 6)
plt.plot([0, 1], [0, 1])


plt.show()

效果展示:

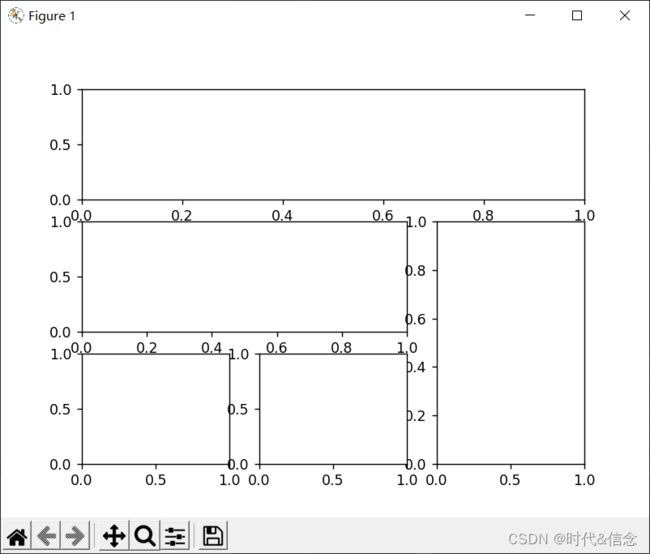
(13)多种形式绘制子图

代码:

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

"""
    在一张图里面画多张图的其他方法
"""


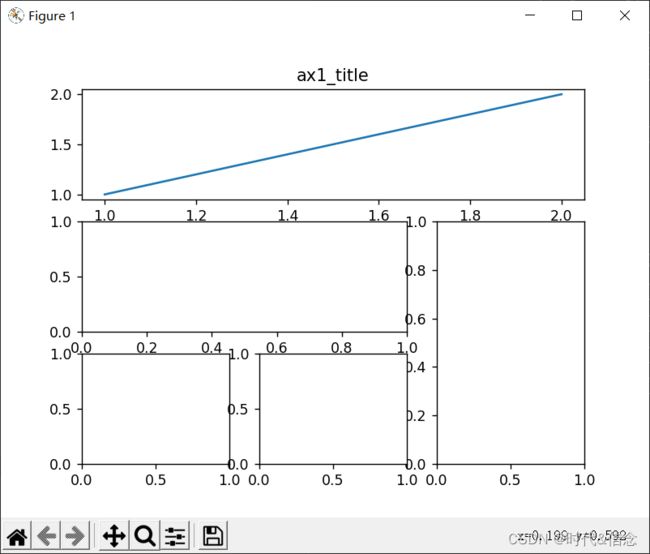
# 方法一：subplot2grid
plt.figure()
# 划定三行三列,其中ax1图在第0行第0列位置,行间距占1,列间距占3
ax1 = plt.subplot2grid((3,3), (0,0), rowspan=1, colspan=3)
# 绘制ax1的图形
ax1.plot([1, 2], [1, 2])
# 设定ax1图片的标题
ax1.set_title("ax1_title")
ax2 = plt.subplot2grid((3, 3), (1, 0), rowspan=1, colspan=2)
ax3 = plt.subplot2grid((3, 3), (1, 2), rowspan=2, colspan=1)
ax4 = plt.subplot2grid((3, 3), (2, 0), rowspan=1, colspan=1)
ax5 = plt.subplot2grid((3, 3), (2, 1), rowspan=1, colspan=1)

plt.show()

效果展示:

代码:

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

"""
    在一张图里面画多张图的其他方法
"""

# 方法二：类似切片的形式
plt.figure()
gs = gridspec.GridSpec(3, 3)
ax1 = plt.subplot(gs[0, :])
ax2 = plt.subplot(gs[1, :2])
ax3 = plt.subplot(gs[1:, 2])
ax4 = plt.subplot(gs[-1, 0])
ax5 = plt.subplot(gs[-1, -2])
plt.show()

效果展示:

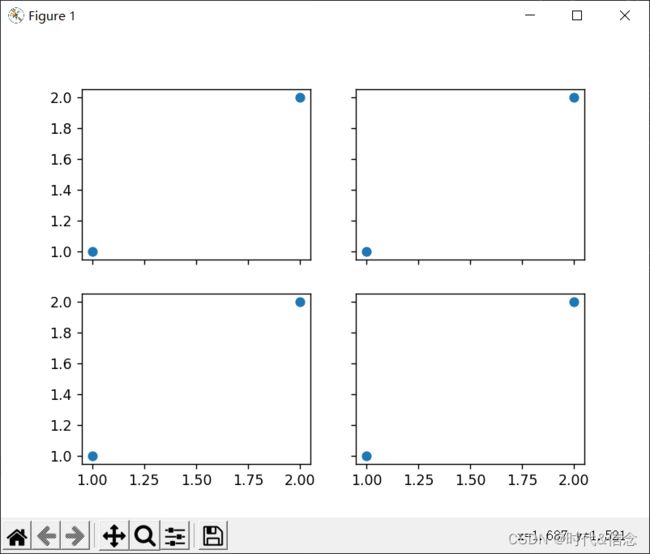
代码:

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

"""
    在一张图里面画多张图的其他方法
"""
# 方法三：
# 共享X轴和Y轴
f, ((ax11, ax12), (ax21, ax22)) = plt.subplots(2, 2, sharex=True, sharey=True)
ax11.scatter([1, 2], [1, 2])
ax12.scatter([1, 2], [1, 2])
ax21.scatter([1, 2], [1, 2])
ax22.scatter([1, 2], [1, 2])

plt.show()

效果展示:

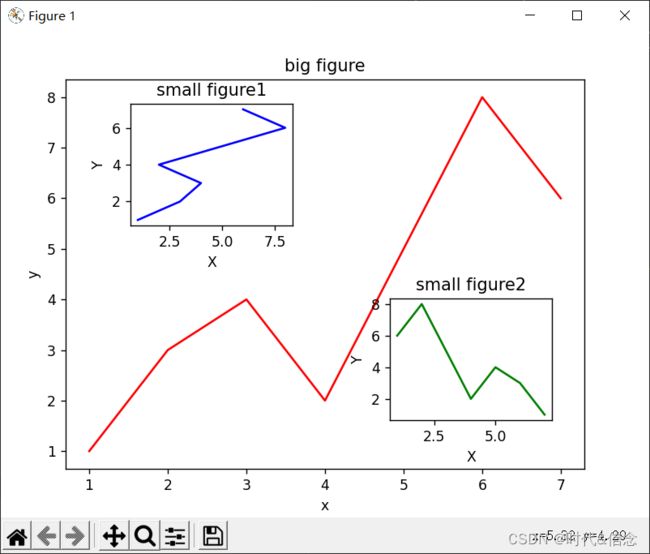
(14)绘制图中图

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
x = [1, 2, 3, 4, 5, 6, 7]
y = [1, 3, 4, 2, 5, 8, 6]

left, bottom, width, height = 0.1, 0.1, 0.8, 0.8
ax1 = fig.add_axes([left, bottom, width, height])
ax1.plot(x, y, 'r')


# 设置x轴y轴描述信息
plt.xlabel("x")
plt.ylabel("y")
plt.title("big figure")


# 绘制图中图，小图1
# 设置图像对应的位置，这里使用的是百分比
left, bottom, width, height = 0.2, 0.6, 0.25, 0.25
ax2 = fig.add_axes([left, bottom, width, height])
ax2.plot(y, x, "b")
ax2.set_title("small figure1")
ax2.set_xlabel("X")
ax2.set_ylabel("Y")


# 小图2
left, bottom, width, height = 0.6, 0.2, 0.25, 0.25
plt.axes([left, bottom, width, height])
plt.plot( x, y[::-1], "g")
plt.title("small figure2")
plt.ylabel("Y")
plt.xlabel("X")

plt.show()

效果展示:

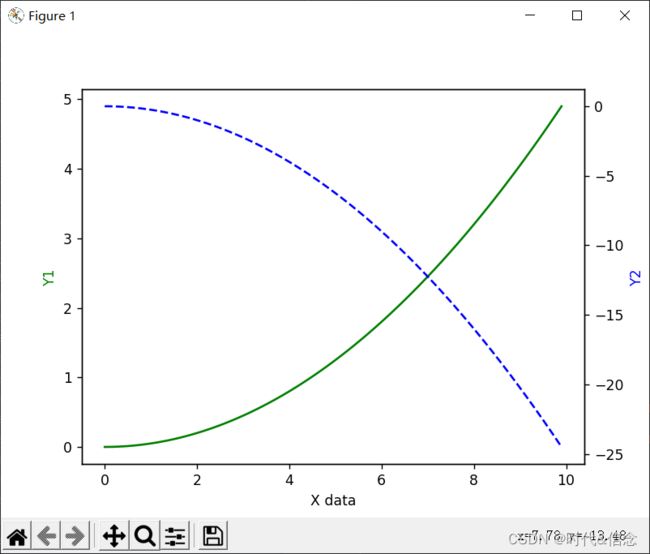
(15)次坐标轴

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np

"""
    次坐标轴
"""

x = np.arange(0, 10, 0.1)
y1 = 0.05 * x ** 2
y2 = -5 * y1

fig, ax1 = plt.subplots()
# 让ax2与ax1共享x坐标轴！！！
ax2 = ax1.twinx()
ax1.plot(x, y1, 'g-')
ax2.plot(x, y2, 'b--')

ax1.set_xlabel("X data")
ax1.set_ylabel('Y1', color="g")
ax2.set_ylabel('Y2', color="b")

plt.show()

效果展示:

(16)绘制动态图

代码:

# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import animation


"""
    使用动画显示数据
"""
# 生成子图，相当于fig = plt.figure(),ax = fig.add_subplot(),其中ax的函数参数表示把当前画布进行分割
fig, ax = plt.subplots()

# 范围是0~2π， 步长为0.01
x = np.arange(0, 2*np.pi, 0.01)
line, =ax.plot(x, np.sin(x))

def animate(i):
    line.set_ydata(np.sin(x+i/10))
    return line,

def init():
    line.set_ydata(np.sin(x))
    return line,




# 生成动画
'''
函数FuncAnimation(fig,func,frames,init_func,interval,blit)是绘制动图的主要函数，其参数如下：
    a.fig 绘制动图的画布名称
    b.func自定义动画函数，即程序中定义的函数animate
    c.frames动画长度，一次循环包含的帧数，在函数运行时，其值会传递给函数animate(i)的形参“i”
    d.init_func自定义开始帧，即传入刚定义的函数init,初始化函数
    e.interval更新频率，以ms计
    f.blit选择更新所有点，还是仅更新产生变化的点。应选择True，但mac用户请选择False，否则无法显示
'''
ani = animation.FuncAnimation(fig=fig, func=animate, frames=100, init_func=init, interval=20, blit=True)

plt.show()

效果展示:

3.Matplotlib总结完毕,撒花!!!