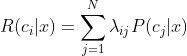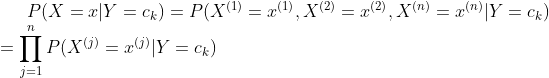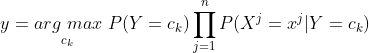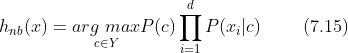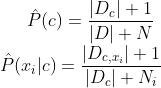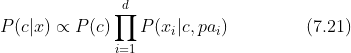【机器学习-西瓜书】第7章 贝叶斯分类器
7.1 贝叶斯决策论 (Bayesian Decision Theory)
在所有相关概率都已知的情况下，贝叶斯决策论考虑的是：如何基于这些概率和误判损失来选择最优的类别标记。
以多分类任务为例解释BDT的基本原理
表示 将真实标记 cj 的样本误分类为 ci 所产生的损失。基于后验概率 
可得到 将样本 x 分类为 ci 所产生的期望损失：
我们的目标是：寻找一个判定准则 
以最小化总体风险：
![R(h) = E_{x}[R(h(x)\ |\ x)]](http://img.e-com-net.com/image/info8/cd79851c364b4d40a50295544ecaebd6.gif){kind=small}
贝叶斯判定准则：为最小化总体风险，只需 在每个样本上选择那个能使条件风险 R( c|x )最小的类别标记：
此时，
称为贝叶斯最优分类器 (Bayes optimal classifier)，即对每个样本 x， 选择能使 后验概率 P( c|x ) 最大的类别标记。
discriminative models：给定 x， 通过直接建模 P( c|x ) 来预测c。比如 决策树、BP神经网络、SVM等
generative models：先建模 联合概率分布 P(x, c)，然后由此获得 P（ c|x )。比如贝叶斯分类器。
根据贝叶斯定理，有
其中，P(c)表示 类先验prior概率；P(x|c)表示 样本x 相对于 类标记c 的类条件概率，也称为“似然”（likelihood），P(x) 表示归一化证据evidence因子。
别注：若加上属性条件独立性假设（同时也是朴素贝叶斯的基本假设），则有
d 表示属性数目，xi 表示 x在第 i 个属性上的取值。
类先验概率P(c) 反映了样本空间中 各类样本所占的比例，当训练集足够大时，可通过各类样本出现的频率来估计。
类条件概率P(x|c) 由于涉及关于x所有属性的联合概率，所以直接根据有限的训练样本出现频率来估计 将十分困难。
7.2 极大似然估计 (Maximum Likelihood Estimation)
如何估计 类条件概率？
一种常见策略是：先假定其具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。即 先假设 P( x|c ) 具有确定的形式，且被参数向量 
唯一确定，于是问题变为：利用训练集 D 估计参数 。
在参数估计问题上，有两个学派：
- 频率主义 学派 (Frequentist)：参数虽未知但固定，因此可通过 优化似然函数来确定参数。
- MLE：根据数据采样 来估计概率分布参数
- 贝叶斯学派 (Bayesian)：参数是 未观察到的随机变量，可先假定参数服从一个先验分布，然后基于观测到的数据来计算参数的后验分布。
MLE
令 
表示 训练集 D 中第 c 类样本组成的集合，假设样本 服从 i.i.d.，则参数 对数据集
的似然，及对数似然为：
此时，参数 的极大似然估计 
为：
现实任务中，要想 所假设的概率分布较好地接近潜在的真实分布，关于任务本身的先验知识是否正确且充足 将十分关键。
7.3 朴素贝叶斯分类器
是典型的生成学习方法：利用训练数据学习 P( X|Y ) 和 P( Y ) 的估计，得到联合概率分布
P( X, Y )= P( Y ) P( X|Y )
利用贝叶斯定理 和 学习到的联合概率分布，来进行分类预测：
基本假设是属性条件独立性 (attribute conditional independence assuption)：对于已知类别， 假设所有属性相互独立。即 假设每个属性独立地对分类结果产生影响。
将 x 分类到后验概率最大的类y，即朴素贝叶斯分类的表达式为：
换言之，基于式（7.6）以及式（7.14），表达式也可写为：
此时，不难计算出 类先验概率P(c)
对离散属性而言，
表示 中在第 i 个属性上取值为 
的样本组成的集合，则
对连续属性则考虑概率密度函数，有
其中，
和 
分别表示 第 c 类样本在第 i 个属性上取值的均值和方差。
smoothing：避免 因训练集样本不充分(有未出现的属性值)，而导致概率估值为零
比如说：Laplacian correction
N 表示训练集 D 中 可能的类别数；Ni 表示第 i 个属性可能的取值数。
7.4 半朴素贝叶斯分类器 (semi-naive Bayes classifier)
尝试对属性条件独立性假设进行一定程度的放松：“独依赖估计”（One-Dependent Estimator）。“独依赖”指的是：假设每个属性在类别之外，最多仅依赖于一个其他属性，即
这里，
是属性 所依赖的属性，称为 的父属性。
如何确定每个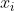属性 的父属性 ？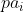
假设 所有属性都依赖于同一个属性，称为 “超父”（super-parent），通过交叉验证等模型选择方法来确定超父属性，即 SPODE (Super-Parent ODE)方法。
在最大带权生成树 (maximum weighted spanning tree)算法的基础上，通过以下步骤约简 属性间的依赖关系，称为 TAN (Tree Augmented Naive Bayes)。
式（7.22）的条件互信息刻画了 属性 和 
在已知类别情况下的相关性。
AODE (Averaged One-Dependent Estimator)是一种 基于集成学习机制、更为强大的独依赖分类器。它尝试 将每个属性作为超父来构建 SPODE，然后将那些有足够训练数据支撑的 SPODE 集成起来作为最终结果，即
表示 在第 i 个属性上取值为 的样本集合，m' 是阈值常数
朴素贝叶斯 vs. 半朴素贝叶斯
7.5 贝叶斯网 (Bayesian network, belief network)
借助 有向无环图 (Directed Acyclic Graph, DAG) 来刻画属性之间的依赖关系，并使用条件概率表 (Conditional Probability Table, CPT) 来描述属性的联合概率分布。
网络结构 G ：一个有向无环图，其每一个结点对应于一个属性，属性间的依赖关系由边edge连接；参数 Θ ：定量描述了属性之间的某种依赖关系。
7.5.1 结构：刻画了属性间的依赖关系
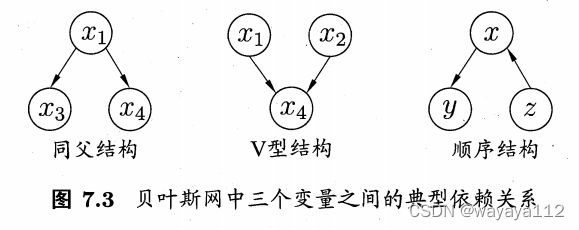
上图的联合概率分布可定义为：
三个典型的贝叶斯网依赖关系
7.5.2 学习
现实应用中，网络结构不易获知，因此 贝叶斯网学习的首要任务是：根据训练集找到结构最合适的贝叶斯网。“评分搜索”便是一种常用办法，具体说来
先定义一个评分函数 (score function，可看做一种归纳偏好)， 用于评估贝叶斯网 与 训练数据的契合程度，然后 基于该评分函数来寻找结构最优的贝叶斯网。
7.5.3 推断
7.6 EM算法 (Expectation Maximization)
现实应用中，遇到“不完整”的训练样本，即当存在“未观测变量” (latent variable)的情形下，可否对模型参数进行估计？
令 X 表示 已观测变量集，Z 表示 隐变量集， Θ 表示模型参数，对 Θ 做极大似然估计，即需要最大化对数似然：
EM 算法
是一种迭代式方法，基本想法是：若参数 Θ 已知，则 可根据训练数据推断出 最优隐变量 Z 的值 (E步); 若 Z 的值已知，则 可以对参数Θ进行极大似然估计 (M步)。
---------------------------------------------------------分割线---------------------------------------------------------------
---------------------------------------------------------分割线---------------------------------------------------------------