太极图形课S1第06讲:光线追踪的概念与基础
序
总觉得,这个以后能用的上
视频
太极图形课S1第06讲:光线追踪的概念与基础_哔哩哔哩_bilibili
代码
GitHub - taichiCourse01/taichi_ray_tracing
averagePerson/taichi_ray_tracing (gitee.com)
感性上,会运行出来这些;看着挺高级的……
但,我是小白,凑凑热闹就行
正文
光追, 没啥耦合的,适合入门。
光栅化:
光追:
图形学,图个漂亮;光线追踪,漂亮,所以说光追……
光追与真实感图形学
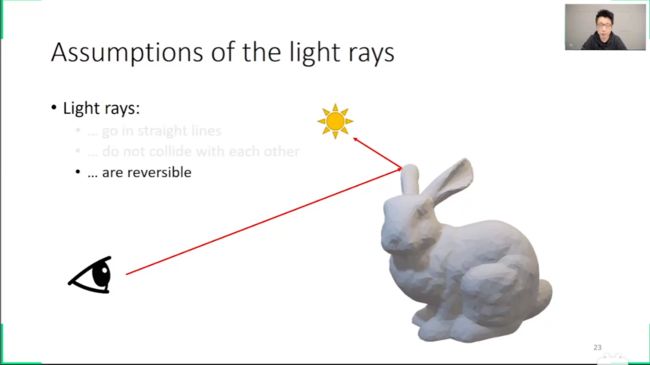
光追的假设
- 所有的光都走直线(不考虑衍射)
- 光与光,相互不碰撞(干涉)
- 光路可逆
光路可逆
古代就有个类似的学说
触觉:手伸出去,所以摸到东西了
所以,用触觉去类比视觉
视觉:眼睛发射出了什么东西,所以感觉到了东西的颜色
光追的思想和这个类似的
光追,追的是这个光线看的到底是什么颜色
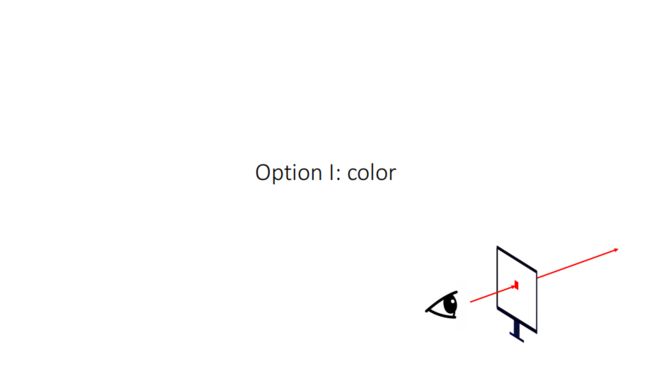
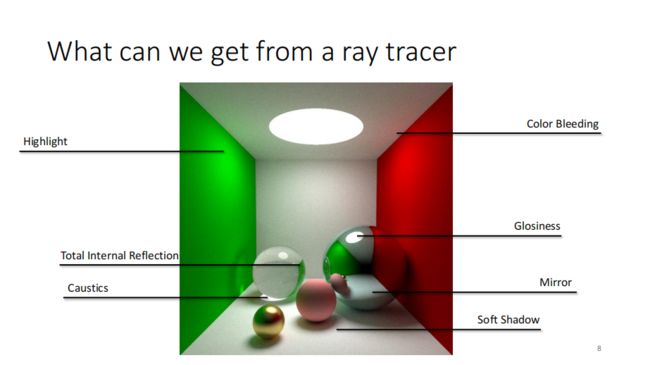
第一部分——颜色
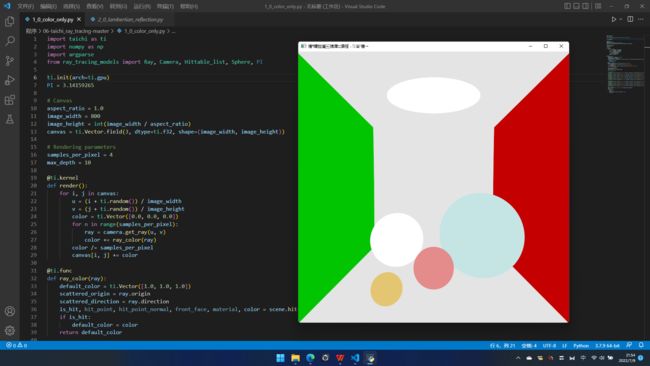
光线追到了光源——白色
光线追到了球——球的灰色
光线追到了空——黑色
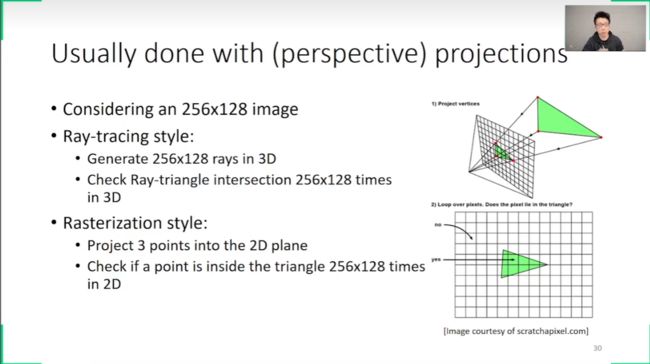
光追与光栅化
上面的光追方法,追出来的就是这个,没啥真实感,为什么?
没有阴影算一个原因
A和B一样白,就是阴影。
认知问题,看到的到底是什么?
win的绘图里的调色板,都是这种结构:2D的颜色+1D的亮度
有了颜色与亮度,就会有阴影的效果了
第二部分——颜色+阴影
有个叫朗博反射模型的,和阴影有关(这个朗博,和朗博比尔有关系吗?)
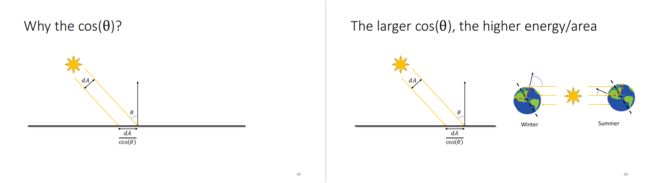
大概就是,夹角和接受到的能量有关,能量守恒
夹角大,就是冬天;夹角小,就是夏天
实际运行。达到了一些古早3D游戏的效果。
其实,按设定来说,它们分别是金属球,玻璃球,黄铜球;但是看上去都是橡胶球……
为什么?因为这里只有漫反射,没有高光
后视镜,某个角度最刺眼,这个就是高光,和角度有关
为了提高计算速度,用角平分线代替了反射光线,这个改进就叫布林-冯模型
2D情况下,这两个θ是一半的比例,总体是成正比的
混合到一起:
ambient:自己的颜色
diffuse:朗博模型
specular:冯模型
【为什么要用球,可能是因为球的法向量比较容易计算】
运行:
看上去真了一点,但是,还有个问题,这个球看上去像漂浮的,因为没有影子
没有影子,就不真实……
所以——
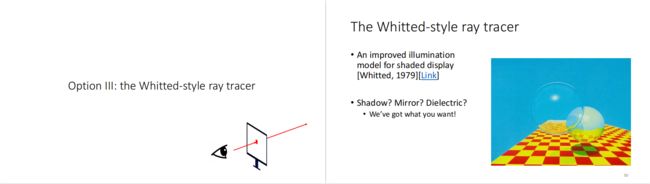
第三部分——光线跟踪
现代GPU,可以100fps+
按上面那个原理,可以算出这个
有了阴影,就不会觉得球在飘着了,就脚踏实地了。
那个不怎么黑的阴影,是因为它是个玻璃球,是透明的,挡的不是那么严实
其它的都是实心的,所以影子非常的黑
在此基础上,还可以接着反射,也就是递归
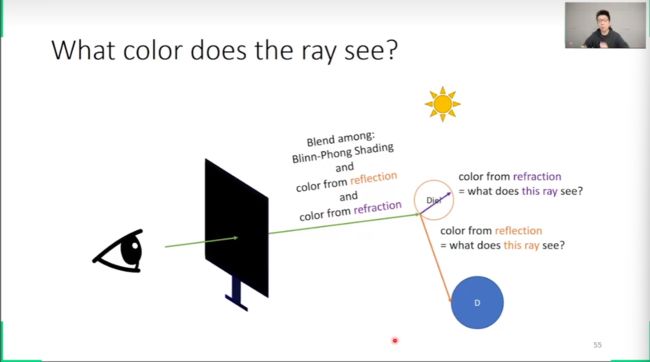
混合和这条光线有交的东西
如果是介电质(玻璃弹珠)
既会发生反射,也会发生折射
多混合一项就行
无限递归,直到明白这个光线到达光源,或者到达虚空,可以确定这条光线的颜色为止
按这个,可以算出这个
古典的ray tracer,就到此为止了;但是现代的RT,比如3090的RT,比这个更精妙
同时,还有个问题……
这个朗博着色,布林冯着色,不是一回事。。有点强行混合的意思,得调一些参数
- 天花板是黑的
- 盒子与天花板的颜色,太泾渭分明了
- 虽然有这么大的一个光源,但是阴影依旧非常的硬
- 玻璃球下面没有聚光的效果
大作业的时候,只弄了镜面反射的金属实心球,还没有天花板,也没有墙,有也是镜面反射的,刻意规避了这些问题……所以没意识到。
第四部分——路径追踪
之前的那些,虽然有问题,但也有合理的部分,可以扬弃一下
- 亮度很重要
- 递归计算光线颜色
但也有大的问题,它假设光到了漫反射表面就结束了。【在渲染结果上就反映为黑色的天花板,与颜色泾渭分明的盒子壁】
而真实的世界里不是这样的,漫反射也是反射
游戏里全局光照的意思,就是控制漫反射是否是光线的结束
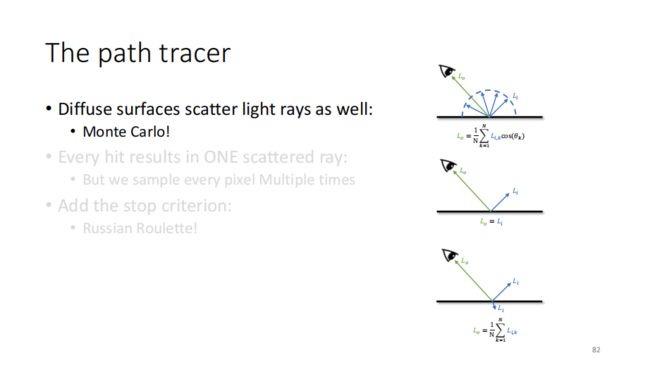
那末,如何模拟漫反射?
——辐射度量学,可以推导出来的……
蒙特卡洛法
python多进程计算pi的时候了解过
造核弹的时候提出来的?……
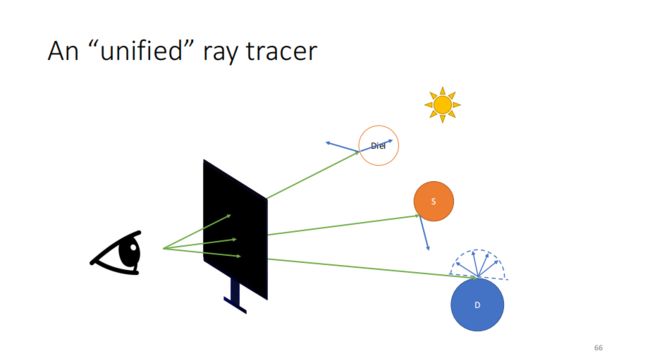
然后,就统一起来了
没完,还有问题
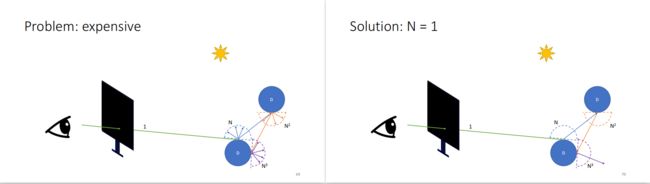
问题1——多次漫反射的光线数按指数增加来的,计算量太大
解决方法1
N=1
但是会计算出类似这样的问题:
为什么?假如光线打到了墙上,如果漫反射到了灯上就会很亮;如果漫反射到了虚空里就会很暗,N=1的随机性太强……
解决方法2
如何改进?
依旧取N=1,但是每个像素多次采样计算平均值(SPP)
当N=1,SPP=100时,可以计算出这个,差不多了。
问题2——返回的条件
到达灯光——返回
到达虚空——返回
无限反弹呢?——没有出口的递归,死循环
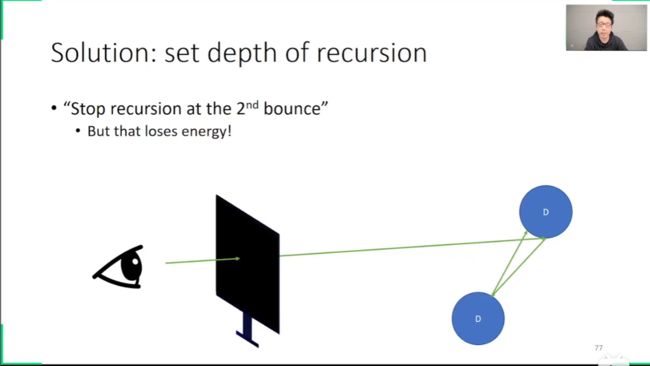
解决方法1
设置一下,比如最多弹2次
这么搞的话,亮度就和设置的深度有关了
也就是说,能量损失了
从渲染结果上来看,就是8的比5的结果要亮
![]()
解决方法2
所以,还有更好的解决方法吗?——俄罗斯轮盘赌
用这个方法,因为它除了一下概率,所以是能量守恒的,就解决了能量损失的问题
总结
——如果有的光线,玩了100把俄罗斯轮盘还没死,可以直接掐死。所以这个俄罗斯轮盘赌和递归深度值,有的时候可以一起用,双保险
计算结果
总结
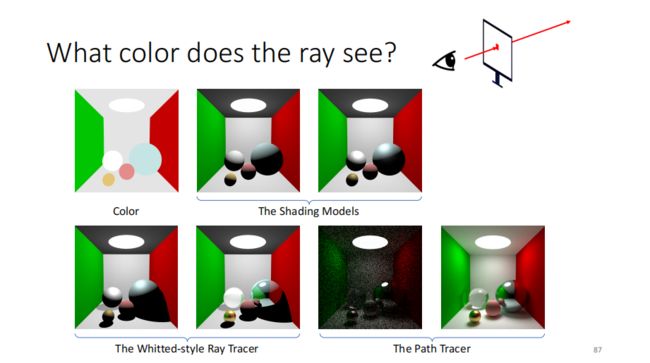
主旨——从眼睛发射一条光,追着它问它是什么颜色的,直到问出来为止
第一行:光栅化
第二行:RT
这个只是概念,还有很多实现细节,下次再说
辐射度量学,再深入,就需要这个了
ray trace in one week,三部曲,越来越恐怖,从入门到终身。。入土。。
都是大佬……